Семантика баз данных

12.2.3 Другие модели, эмулируемые в иерархической модели данных

СУБД Cache обладает уникальными особенностями, которые позволяют существенно расширить ее возможности. Использование двух моделей—объектной и реляционной, обычная вещь в сегодняшних базах данных. Неразрывная связь этих моделей и еще иерархической модели — явление уникальное. Еще важнее то, что имеет эффективный язык для работы с деревьями, позволяющий организовывать многопоточную работу, но иерархическая модель данных не организована. Это позволяет, используя COS, расширить возможности СУБД Cache за счет введения практически любых моделей данных и усилить технологическое оснащение программирования за счет разработки транслятора для любой парадигмы.

Как и в реализации полуструктурированной модели, описанной выше, для эмулирования других моделей в иерархической модели необходимо деревья Cache пополнить различными ссылками. При этом в двухсторонних (т.е. неориентированных) ссылках при добавлении ссылки из одного узла на другой в последнем должна автоматически появляться ссылка на первый узел. Это обеспечивает навигацию по любым путям.

Обратим внимание на то, что универсальная модель данных, представленная на рисунке 12.1, это дерево с четырьмя уровнями: "схема" (это корень), "таблица", "столбец", "данные" (имеется в виду значение в ячейке на пересечении строки и столбца). Отсюда понятно, как в иерархической модели эмулировать модели табличного типа, объектные и объектно-реляционные модели.

В наиболее развернутом варианте глобал, эмулирующий сеть, делится на два поддерева — ветвей и узлов. Узлы ветвей, находящиеся на первом уровне, содержат описания всех связей с их именами, арностями, атрибутами привязки к узлам, именами этих узлов и эмерджентными атрибутами связей. Поддерево узлов содержит описания узлов со значениями в виде списка связей, в которых он участвует.

Во втором способе узлы сети и их значения находятся на первом уровне дерева. В первом подварианте (будем говорить о подходе от значений) информация о том, что элементы (a₁,a₂, . . . ,а_n) находятся в ориентированном отношении с именем р, хранится как часть значения узла a₁. Во втором подварианте (подход от индексов) эти сведения размещаются в индексах потомков узла a_j. Если сеть хранится в глобале ^Р, то такое отношение будет храниться как узел ^P(a₁,a₂, . . . ,а_n) со значением р. Если этот набор узлов связан несколькими отношениями, то они перечисляются в значении узла ^P(a₁,a₂, . . . ,а_n) через запятую. Если отношение неориентированное, то информация о нем хранится в каждом из узлов, участвующих в отношении.

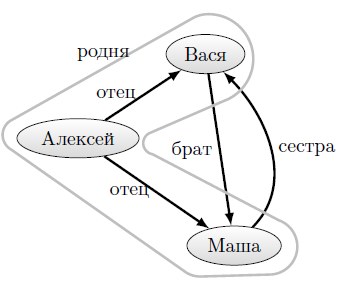
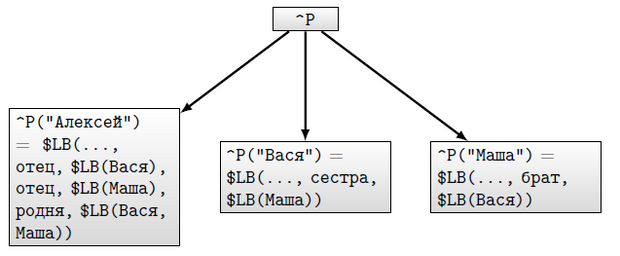
На рисунке 12.12 в качестве примера показана сеть из трех узлов, представляющих трех человек — Алексея, Васю и Машу. На рисунке 12.13 изображено дерево, представляющее эту сеть при хранении ссылок в индексах дерева. Заметим, что отношения "родня" не ориентированное, так что можно было добавить еще пять узлов уровня 3 или ввести глобал справочника, позволяющий установить наличие такого отношения. На рисунке 12.14 —та же сеть, но расположенная в дереве с хранением информации о ссылках в значениях узлов. Первым элементом этого списка значений будет элемент, характеризующий узел сети, но не отношения, в которые он входит (на рисунках 12.13 и 12.14 эта часть представлена многоточием). На четных позициях, начиная со второй, помещаются имена отношений, на следующих за ними нечетных — списки узлов, входящих в отношения с предш ествующим именем. Выбор такого представления обусловлен тем, что поиск по равенству выполняется непосредственно функцией $LISTFIND.

Рис. 12.12. Пример сети

увеличить изображение
Рис. 12.13. Пример хранения ссылок сети в индексах

Рис. 12.14. Пример хранения ссылок сети в узлах

Моделирование отношений произвольной арности позволяет представлять гиперграфы и семантические сети. Можно представлять наборы 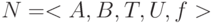, где

• — конечное множество вершин;
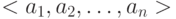• — множество кортежей , где 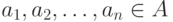. Каждый кортеж соответствует вершинам сети, которые находятся в некотором отношении;
• — конечное множество имен отношений;
• — мультимножество, состоящее из элементов ;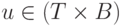
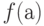• — функция, которая каждой вершине 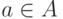ставит в соответствие некоторое значение. Это значение, в зависимости от интерпретации может быть и набором параметров и именем функции, которую нужно вызвать.

Как уже упоминалось, в неориентированных отношениях каждый узел содержит ссылки на все остальные узлы, связанные этим отношением. Из-за большой избыточности такого представления предлагается использовать вариант описанного выше представления с двумя поддеревьями: одно — для хранения узлов, другое —для неориентированных отношений. Ориентированные отношения хранятся как обычно, а неориентированные как ссылки на одноуровневые деревья, узлами которых являются имена узлов, состоящих в данном отношении.

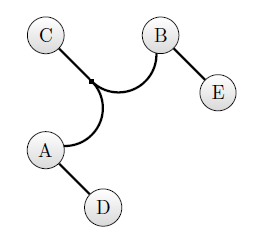
На рисунке 12.15 изображен гиперграф, а на рисунке 12.16 — дерево, представляющее этот гиперграф. Ориентированные отношения хранятся в нем в узлах. На неориентированные отношения дается только ссылка. Эта ссылка представляет собой список из двух элементов: первый —это имя отношения, а второй — номер набора элементов для этого отношения.

Рис. 12.15. Пример гиперграфа

увеличить изображение
Рис. 12.16. Часть структуры хранения гиперграфа

На основе предложенного подхода в Cache могут быть реализованы двудольные графы сетей Петри. Необходимо организовать представление фишек и создать автомат, обеспечивающий работу сети.

Фишки, в том числе разносортные, представляются значениями узлов. В варианте с хранением сети в одном глобале индексы мест сети Петри получают префикс "Р_", а переходы снабжаются префиксом "В_". В результате автоматической сортировки узлов все переходы располагаются левее всех мест. Естественно, в реализации использовано ограничение "ребра между однотипными узлами не существуют". Возможны два варианта обхода сети — синхронный и асинхронный. Синхронный обход может быть реализован методом, использующим функцию $ORDER, которая в цикле перебирает всех потомков корневого узла, представляющих переходы сети. Для каждого такого узла анализируется возможность перехода и при положительном решении переход выполняется.

Для изменения порядка обхода узлов, представляющих переходы, достаточно расширить префикс. Изменение порядка обхода при необходимости может быть выполнено "на ходу" путем переписывания графа. Другой вариант — задание списка вершин для обхода параметром метода, выполняющего обход.

Асинхронный обход моделируется набором фоновых процессов, запускаемых операторами job. Каждый процесс следит за одним или несколькими переходами и через заданный интервал времени пытается выполнить свой переход. Для уменьшения нагрузки процессора, могут быть введены задержки.

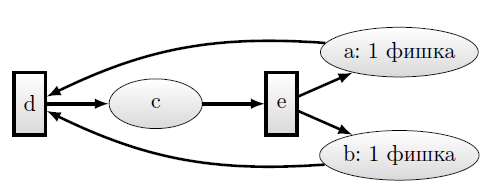
Пример простой сети Петри, и ее представление в Cache приведены на рисунках 12.17 и 12.18. В значениях узла первый элемент для переходов—пустая строка, а для мест —количество фишек. "link" —имя отношения, необходимое для организации ссылки.

Рис. 12.17. Пример сети Петри

Рис. 12.18. Пример хранения сети Петри

Обратим внимание, что эмуляция моделей в глобалах требует существенного изменения семантики данных, которая должна интерпретироваться приложением. Это требует написания значительного объема программного кода.