Комбинаторная логика как формальная система

Перечислим правила вывода комбинаторных термов, которые задают характеристики отношения конвертируемости:

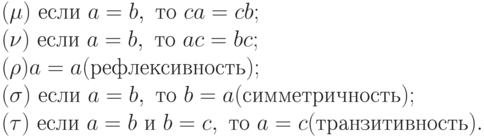
Как видно из перечисленных выше свойств, отношение конвертируемости обладает, в частности, свойствами рефлексивности, симметричности и транзитивности. Первое из только что перечисленных свойств означает конвертируемость произвольного комбинаторного выражения к самому себе, второе - двунаправленность вывода комбинаторных выражений посредством конверсии, а третье - возможность опускать промежуточные этапы конверсии для цепочек вывода.

К сожалению, относительная простота описания предыдущих этапов формальной теории комбинаторной логики ( алфавита, аксиом и правил вывода ) порождает довольно громоздкие выкладки при моделировании вычислений.

В этой связи из соображений экономии пространства для вывода соотношений принимаются следующие умолчания, позволяющие значительно сократить запись и увеличить удобство прочтения и обработки комбинаторных термов.

Во-первых, скобки для операции аппликации восстанавливаются по ассоциации влево, например:

XY = (XY), XYZ = ((XY)Z), ...

Во-вторых, избыточные скобки могут опускаться, например:

(XY) = XY, ((XY)Z) = XYZ, ...

Под синтаксисом понимают раздел описания формального математического языка или языка программирования, исследующий вид, форму и структуру конструкций, без учета их значения (или, иначе, семантики ) или практической применимости (или, иначе, прагматики ).

Задать синтаксис языка возможно, перечислив описание его конструкций, например, с помощью форм Бэкуса-Наура или БНФ. БНФ созданы в 60-х годах Дж. Бэкусом (John Backus) и развиты П. Науром (Peter Naur) как метаязык для формализации синтаксиса языка программирования ALGOL 60. Впоследствии БНФ получили широкое распространение и в настоящее время являются основной нотацией для формализации синтаксиса языков программирования (мы будем пользоваться БНФ для формализации синтаксиса языка программирования SML). В данной нотации символ " ::= " интерпретируется словами "может иметь вид", а символ " | " - словом "или". Определяемое и определяющие понятия записываются в угловых скобках, первое - слева, а последние - справа от значка " ::= ".

Формализуем синтаксис   выражений комбинаторной логики (или комбинаторов ).

БНФ -описание комбинатора имеет вид:

<комбинатор> ::= K | S | (<комбинатор> <комбинатор>)

БНФ -описание терма комбинаторной логики, возможно, содержащего переменные, имеет вид:

<комбинаторный терм> ::= K | S | <переменная> |
  (<комбинаторный терм> <комбинаторный терм>)

Проиллюстрируем представленную формальную систему комбинаторной логики необходимыми примерами комбинаторов. Рассмотрим характеристические соотношения для комбинаторов, которые впоследствии окажутся теоретически интересными и практически полезными в данном курсе (некоторые из соотношений совпадают с введенными ранее аксиомами ):

(I)	I a = a; 
(K)	К ab = a;
(S)	S abc = ac(bc); 
(B)	B abc = a(bc); 
(C)	C abc = acb;
(W)	W xy = xyy.

Соотношение (I), как уже отмечалось, характеризует комбинатор   тождества.

Соотношение (K), как отмечалось, характеризует комбинатор первой проекции (иначе именуемый канцелятором, т.е. "отменяющим" "выполнение" всех "инструкций", кроме первой).

Соотношение (S) характеризует комбинатор - коннектор, который определяет порядок "связывания" "инструкций" программы таким образом, что третья "инструкция" "распределяется" по паре из двух первых.

Соотношение (B) характеризует комбинатор   композиции, который образует последовательность комбинаторных термов и служит для объединения более элементарных "инструкций" в более сложные, а в итоге - в "программы".

Соотношения (C) и (W) определяют соответственно пермутацию ( перестановку ) и дублирование аргументов.

Напомним, что одной из основных причин возникновения ламбда-исчисления была необходимость исследовать возможность кратчайшей перезаписи выражения ( функции ) с сохранением эквивалентного значения. Для реализации этой возможности вводилось преобразование редукции ламбда- термов.

Оказывается, что в комбинаторной логике наследуется возможность редукции. Поскольку она интересна теоретически (для сокращения выкладок) и полезна практически (для оптимизации программного кода абстрактных машин ), рассмотрим ее более подробно.

В ходе исследований выяснилось, что редукция (преобразование для сокращения записи) комбинаторных термов возможна в соответствии с правилами вывода, аналогичными аксиомам   (K) и (S).

Проиллюстрируем моделирование механизма редукции следующим примером.

Рассмотрим комбинаторный терм вида

SKKx.

Пользуясь аксиомами   (К) и (S), а также правилами вывода, произведем редукцию   терма:

SKKx = (по правилу S)
Kx(Kx) = (по правилу K)
x.

В результате получаем, что SKKx = x, откуда, с учетом аксиом и правила (I), I = SKK.

Как видно из предыдущего примера, одни комбинаторы можно выразить через другие.

Возникает вопрос: существует ли конечный набор комбинаторов, посредством которого можно выразить произвольный терм комбинаторной логики? Оказывается, что ответ на поставленный вопрос утвердителен, причем введенные аксиомы и правила вывода обеспечивают весьма лаконичный набор такого рода.

Необходимость продолжения рассуждений приводит нас к понятию базиса.

Множество (минимальной мощности) комбинаторов, через элементы которого может быть выражен произвольный комбинатор, называется ( минимальным ) базисом .

Оказывается, можно доказать, что:

1. базис   термов для комбинаторной логики действительно существует (причем существует бесконечное множество возможных базисов );
2. для любого базиса справедливо, что он обеспечивает представление произвольного комбинаторного терма (в силу свойства полноты, которым обладает система комбинаторной логики);
3. минимальный базис состоит всего из двух "инструкций"- комбинаторов, например, {K,S}.

Приведем еще несколько примеров базисов:

{I,K,S}; {I,B,C,S}; {B,W,K}.

Разложение термов в базисе   {K,S} для ранее рассмотренных комбинаторов имеет вид:

B = S(KS)K; W = SS(K(SKK)); C = S(BBS)(KK).

Разложение в базисе аналогично программированию на языке базисных инструкций.

Выясняется, что комбинаторная логика обладает возможностью не только моделировать процесс реализации программного обеспечения на языке функционального программирования, но и прозрачно формализовать процедуру приписывания типов объектам этого языка.

Под типом ( сортом ) будем понимать относительно устойчивую и независимую совокупность элементов, которую можно выделить во всем рассматриваемом множестве (предметной области). Более подробно типизация языков программирования и теория типов будут рассмотрены нами в ходе следующей лекции.

В случае комбинаторной логики будем считать, что тип   a приписан комбинатору   X тогда и только тогда, когда это утверждение получено из следующих аксиом:

(FI)   ||- #(I) = (a,a),
(FK)   ||- #(K) = (a,(b,a)) = (a,b,a),
(FS)   ||- #(S) = ((a,(b,c)), ((a, b)(a,c)))

и правила вывода

(F)   если ||- #(X) = (a,b) и ||- #(U) = a,
        то ||- #(XU) = b.

Заметим, что процедура контроля соответствия типов транслятора языка программирования реализована сходным образом, причем в ней используется механизм сопоставления с образцом. В языке программирования SML, кроме того, применятся механизм получения логического вывода о типе   выражения, исходя из контекста его использования. Этот механизм, известный также как выводимость типов (type inference), адекватно моделируется в терминах комбинаторной логики.

В качестве иллюстрации естественности применения формальной системы комбинаторной логики для моделирования языка функционального программирования SML приведем определения функций, реализующих характеристики некоторых из базисных комбинаторов:

fun Ix = x;
fun Kxy = x;
fun Sxyz = xz(yz);

Реализация функций достаточно прозрачна и не требует пояснений.

Функция   I реализует комбинатор   тождества   I, функция   K - комбинатор - канцелятор   K, а функция   S - комбинатор - коннектор   S.

Для более подробного самостоятельного ознакомления с тематикой лекции рекомендуется следующий список источников: [32, 43, 44, 76].