|
Постройте таблицу значений функции |
Массивы
Массив – это пронумерованный набор однотипных элементов.
Массивы бывают статическими и динамическими. У статического массива количество элементов известно заранее и не может быть изменено. У динамического массива количество элементов заранее неизвестно и определяется в процессе выполнения программы.
Также массивы различаются по размерности: одномерные, двумерные, трехмерные и т.д. Примером одномерного массива может послужить вектор 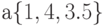 . Примером двухмерного массива может послужить матрица. Примером трехмерного массива может послужить набор высот местности.
. Примером двухмерного массива может послужить матрица. Примером трехмерного массива может послужить набор высот местности.
Массивы различают по типу элементов. Бывают целочисленные, вещественные (состоящие из дробных чисел), символьные массивы.
Примеры массивов:
- вектор
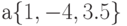 – одномерный вещественный массив из трех элементов;
– одномерный вещественный массив из трех элементов; - матрица
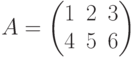 – двумерный целочисленный массив из шести элементов;
– двумерный целочисленный массив из шести элементов; -
 – одномерный символьный массив;
– одномерный символьный массив; -
 – не является массивом, т.к. часть элементов символы, часть элементов числа.
– не является массивом, т.к. часть элементов символы, часть элементов числа.
Мы будем рассматривать только статические одномерные и двумерные численные массивы.
Занятие 1. Одномерные массивы
Индекс – это номер элемента в массиве.
У одномерного массива один индекс, обычно он обозначается  .
.
Чтобы использовать одномерный массив в программе, необходимо:
- объявить массив в функции main():
тип_данных имя_массива[количество элементов]; double a[3]; //статический массив а из трех дробных чисел int b[7]; //статический массив b из семи целых чисел
- проинициализировать массив, т.е. задать каждому элементу конкретное числовое значение;
- провести вычисления, исследования.
Примечание. Индексация в массиве начинается с 0, т.е. индекс у самого первого элемента в массиве  . Индексация в массиве
. Индексация в массиве 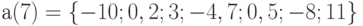 указана на рис. 6.1.
указана на рис. 6.1.
Способы инициализации одномерного массива представлены в табл. 6.1. Обратим внимание на то, что число  известно заранее и в программе фигурировать не будет.
известно заранее и в программе фигурировать не будет.
| Часть блок-схемы | Часть программы |
|---|---|
| 1. инициализация числами |
double a[4]={0.5, -2,856, 1}; |
| 2. с клавиатуры: |
double a[n];
int i;
for(i=0; i<n; i=i+1){
cout<<"a["<<i<<"]=";
cin>>a[i];
} |
| 3. из файла: |
double a[n];
int i;
fstream file;
file.open("1.txt", ios::in);
for(i=0; i<n; i=i+1){
file>>a[i];
}
file.close(); |
| 4. по заданной формуле a[i]=f(i): |
double a[n];
int i;
for(i=0; i<n; i=i+1){
a[i]=f(i);
} |
Примечание. Более подробно работа с файлами будет рассмотрена позже.
Вывод одномерного массива на экран представлен в табл. 6.2.
| Часть блок-схемы | Часть программы |
|---|---|
for(i=0; i<n; i=i+1){
cout<<"a["<<i<<"]="<<a[i]<<endl;
}
|
Принципы нахождения таких величин, как сумма, произведение, минимальное, максимальное значение, представлены в табл. 6.3.
| Часть блок-схемы | Часть программы |
|---|---|
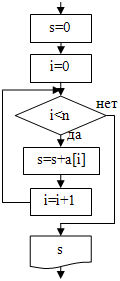
| 1. нахождение суммы: |
s=0;
for(i=0; i<n; i=i+1){
s=s+a[i];
}
cout<<"s="<<s<<endl; |
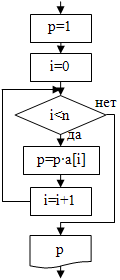
| 2. нахождение произведения: |
p=1;
for(i=0; i<n; i=i+1){
p=p*a[i];
}
cout<<"p="<<p<<endl; |
| 3. нахождение среднего арифметического и количества элементов: |
s=0, k=0;
for(i=0; i<n; i=i+1){
s=s+a[i];
k=k+1;
}
s=s/k;
cout<<"s="<<s<<endl;
cout<<"k="<<k<<endl; |
| 4. нахождение максимального элемента: |
max=-10E10;
imax=0;
for(i=0; i<n; i=i+1){
if(a[i]>max){
max=a[i];
imax=i;
}
}
cout<<"max="<<max<<" imax="<<imax<<endl; |
| 5. нахождение минимального элемента: |
min=10E10;
imin=0;
for(i=0; i<n; i=i+1){
if(a[i]<min){
min=a[i];
imin=i;
}
}
cout<<"min="<<min<<" imin="<<imin<<endl; |
| 6. поменять местами элементы с индексами i1 и i2: |
tmp=a[i1]; a[i1]=a[i2]; a[i2]=tmp; |
7. вычисление формулы ![S=\sum^{n=1}_{i=0}f(a[i],i)](/sites/default/files/tex_cache/31789b72c1e4a1ccda1676153fedc730.png) : :
|
s=0;
for(i=0; i<n; i=i+1){
s=s+f(a[i],i);
}
cout<<"s="<<s<<endl; |
Пример 1. Даны четыре одномерных массива: 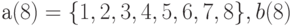 вводится с клавиатуры,
вводится с клавиатуры, 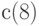 вычисляется по формуле
вычисляется по формуле 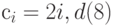 вычисляется по формуле
вычисляется по формуле 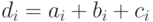 . Построить таблицу значений массивов.
. Построить таблицу значений массивов.
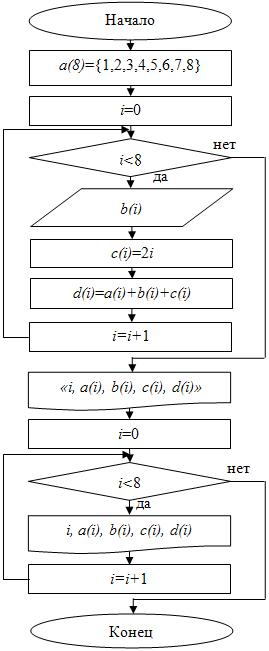
Решение. Сначала необходимо проинициализировать массивы согласно условию задачи.
Массив  задан числами (первый способ инициализации), поэтому он будет проинициализирован при объявлении.
задан числами (первый способ инициализации), поэтому он будет проинициализирован при объявлении.
В цикле по переменной 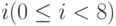 введем
введем  с клавиатуры (второй способ инициализации), массивы
с клавиатуры (второй способ инициализации), массивы  и
и  рассчитаем по формулам (четвертый способ инициализации).
рассчитаем по формулам (четвертый способ инициализации).
Далее организуем еще один цикл по переменной 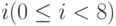 , в котором выведем все проинициализированные массивы на экран.
, в котором выведем все проинициализированные массивы на экран.
Вывод таблицы на экран нельзя делать в первом цикле, т.к. в каждой итерации будет идти запрос очередного элемента  , тогда таблица со значениями массивов будет смешана с запросом элемента
, тогда таблица со значениями массивов будет смешана с запросом элемента  .
.
Блок-схема представлена на рис. 6.2.
Код программы (Visual Studio) с оператором for:
// proga27.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
#include <iomanip>
using namespace std;
int main()
{
double a[8]={1,2,3,4,5,6,7,8};
double b[8], c[8], d[8];
int i;
for(i=0; i<8; i=i+1){
cout<<"b["<<i<<"]=";
cin>>b[i];
c[i]=2.0*i;
d[i]=a[i]+b[i]+c[i];
}
cout<<setw(2)<<"i"<<setw(5)<<"a"<<setw(5)<<"b"<<setw(5)<<"c"<<setw(5)<<"d"<<endl;
for(i=0; i<8; i=i+1){
cout<<setw(2)<<i<<setw(5)<<a[i]<<setw(5)<<b[i]<<setw(5)<<c[i]<< setw(5)<<d[i]<<endl;
}
return 0;
}Результат выполнения программы:
Пример 2. Массив 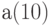 задан формулой
задан формулой 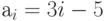 . Вычислить сумму положительных элементов массива и поменять местами первый и последний элементы.
. Вычислить сумму положительных элементов массива и поменять местами первый и последний элементы.
Решение.
Обозначим за  сумму положительных элементов массива. При расчете
сумму положительных элементов массива. При расчете  требуется дополнительное условие: "
требуется дополнительное условие: "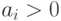 ". Первый элемент массива имеет индекс 0, последний элемент имеет индекс 9, поэтому будем менять местами
". Первый элемент массива имеет индекс 0, последний элемент имеет индекс 9, поэтому будем менять местами  и
и  . Из-за перемены мест элементов массив изменится, поэтому выведем его еще раз.
. Из-за перемены мест элементов массив изменится, поэтому выведем его еще раз.
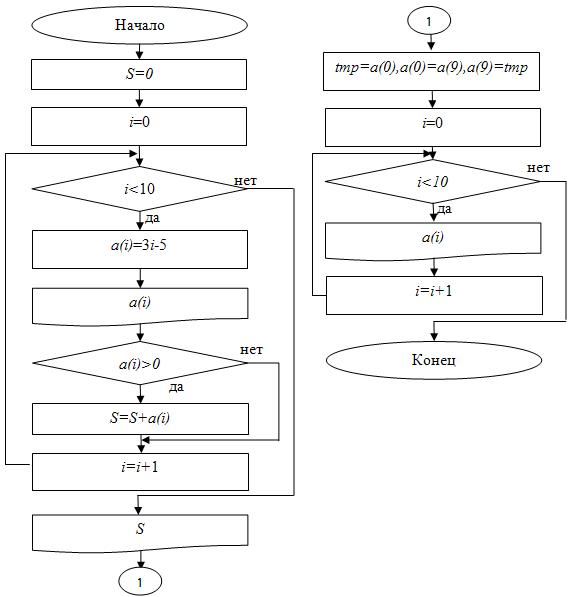
Блок-схема представлена на рис. 6.3.
Код программы (Visual Studio) с оператором for:
// proga28.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
#include <iomanip>
using namespace std;
int main(){
double S, tmp, a[10];
int i;
S=0;
for(i=0; i<10; i=i+1){
a[i]=3.0*i-5.0;
cout<<setw(3)<<a[i];
if(a[i]>0){
S=S+a[i];
}
}
cout<<endl;
cout<<"S="<<S<<endl;
tmp=a[0];
a[0]=a[9];
a[9]=tmp;
for(i=0; i<10; i=i+1){ cout<<setw(3)<<a[i]; }
cout<<endl;
return 0;}Результат выполнения программы:
Ручной счет:
при i=0 a(0)=3i-5=3·0-5=-5; при i=1 a(1)=3i-5=3·1-5=-2; при i=2 a(2)=3i-5=3·2-5=1; при i=3 a(3)=3i-5=3·3-5=4; при i=4 a(4)=3i-5=3·4-5=7; при i=5 a(5)=3i-5=3·5-5=10; при i=6 a(6)=3i-5=3·6-5=13; при i=7 a(7)=3i-5=3·7-5=16; при i=8 a(8)=3i-5=3·8-5=19; при i=9 a(9)=3i-5=3·9-5=22; сумма положительных элементов S=1+4+7+10+13+16+19+22=92.·














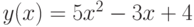 при
при 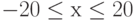 с шагом 0,5. Определите наименьшее значение функции и значение
с шагом 0,5. Определите наименьшее значение функции и значение  , при котором оно достигается.
, при котором оно достигается.