Минимальные остовные деревья

Алгоритм Крускала

Алгоритм Прима строит минимальное остовное дерево по одному ребру, находя на каждом шаге ребро, которое присоединяется к единственному растущему дереву. Алгоритм Крускала также строит MST, добавляя к нему по одному ребру, но в отличие от алгоритма Прима, он отыскивает ребро, которое соединяет два дерева в лесу, образованном растущими MST-поддеревьями. Построение начинается с вырожденного леса из V деревьев (каждое состоящее из одной вершины), а затем выполняется операция объединения двух деревьев (самыми короткими ребрами), пока не останется единственное дерево — MST.

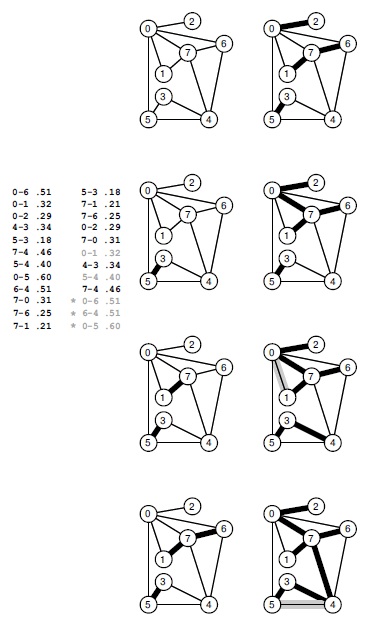
На рис. 20.12 показан пример пошагового выполнения алгоритма Крускала; рис. 20.13 демонстрирует динамические характеристики этого алгоритма на более крупном примере. Разобщенный лес MST-поддеревьев постепенно объединяется в единственное дерево.

Рис. 20.12. Алгоритм Крускала вычисления MST

Пусть задан список ребер графа в произвольном порядке (левый список ребер). На первом шаге алгоритма Крускала они сортируются по весам (правый список ребер). Затем мы просматриваем ребра этого списка в порядке возрастания их весов, добавляя в MST ребра, которые не создают в нем циклов. Сначала мы добавляем ребро 5-3 (самое короткое ребро), потом 7-6 (слева), затем 0-2 (справа вверху) и 0-7 (справа, вторая диаграмма сверху). Ребро 0-1 со следующим по величине весом создает цикл и поэтому не добавляется в дерево. Ребра, которые не включаются в MST, выделены в отсортированном списке серым цветом. Затем мы добавляем ребро 4-3 (справа, третья диаграмма сверху). Далее мы отбрасываем ребро 5-4, поскольку оно образует цикл, и потом добавляем 7-4 (справа внизу). Когда MST-дерево готово, любое ребро с большим весом образует цикл и поэтому будет отброшено (алгоритм останавливается, когда в MST будут включены V— 1 ребер). В отсортированном списке эти ребра помечены звездочками.

Ребра добавляются в MST-дерево в порядке возрастания их длины — таким образом, лес содержит вершины, соединенные друг с другом относительно короткими ребрами. В любой момент выполнения алгоритма каждая вершина расположена ближе к некоторой вершине своего поддерева, чем к любой другой вершине, не входящей в это дерево.

Алгоритм Крускала прост в реализации — при наличии базовых алгоритмических инструментов, рассмотренных ранее в данной книге. Можно использовать любую сортировку из описанных в части 3 для упорядочения ребер по весу и любой из алгоритмов решения задачи связности из "Введение" для удаления циклообразующих ребер. Программа 20.8 содержит соответствующую реализацию функции построения MST для АТД графа, которая функционально эквивалентна другим реализациям MST, рассмотренным в данной главе. Эта реализация не зависит от представления графа: она вызывает клиентскую программу GRAPH, чтобы получить вектор, содержащий ребра графа, а затем на основе этого вектора строит MST-дерево.

Обратите внимание, что существуют два способа окончания работы алгоритма Крускала. Если мы найдем V- 1 ребер, то мы уже построили остовное дерево и можем остановиться. Если мы просмотрим все вершины и не найдем V— 1 древесных ребер, то это означает, что граф не является связным — точно так же, как это сделано в "Введение" .

Рис. 20.13. Алгоритм Крускала вычисления MST

Эта последовательность показывает 1/4, 1/2, 3/4 и полное MST по мере его роста.

Программа 20.8. Алгоритм Крускала вычисления MST

Для отыскания MST эта реализация использует АТД сортировки из "Элементарные методы сортировки" и АТД объединения-поиска из "Абстрактные типы данных" , рассматривая ребра в порядке возрастания их весов и отбрасывая те ребра, которые образуют циклы, пока не будут найдены V— 1 вершин, составляющих остовное дерево.

Здесь не показан класс-оболочка EdgePtr, позволяющий функции sort сравнивать указатели на ребра с помощью перегруженной операции <, как описано в "Элементарные методы сортировки" , и вариант программы 20.2 с третьим шаблонным аргументом.

  template <class Graph, class Edge, class EdgePtr>
  class MST
    { const Graph &G;
      vector<EdgePtr> a, mst;
      UF uf;
    public:
      MST(Graph &G) : G(G), uf(G.V()), mst(G.V())
        { int V = G.V(), E = G.E();
          a = edges<Graph, Edge, EdgePtr>(G);
          sort<EdgePtr>(a, 0, E-1);
          for (int i = 0, k = 1; i < E && k < V; i++)
            if (!uf.find(a[i]->v, a[i]->w))
              { uf.unite(a[i]->v, a[i]->w);
                mst[k++] = a[i];
              }
        }
    };
      

Анализ времени выполнения алгоритма Крускала не представляет трудностей, т.к. известно время выполнения составляющих его операций АТД.

Сравнение производительности алгоритмов Крускала и Прима будет выполнено в разделе 20.6. А пока учтите, что время выполнения, пропорциональное E lgE, не обязательно хуже, чем ElgV: т.к. E не превышает V², то lgE не превосходит 2 lgV Различия в производительности для конкретных графов обусловлены особенностями реализации и тем, приближается ли фактическое время выполнения к граничным значениям для худшего случая.

На практике можно воспользоваться быстрой сортировкой или быстрой системной сортировкой (которая обычно основана на быстрой сортировке). Теоретически такой подход может быть непривлекательным из-за квадратичной трудоемкости сортировки в худшем случае, однако обычно при этом время выполнения уменьшается. Хотя вообще-то можно воспользоваться поразрядной сортировкой, чтобы выполнить упорядочение ребер за линейное время (при определенных ограничениях на веса ребер) — тогда будут превалировать затраты на выполнение E операций найти. Это позволит изменить формулировку леммы 20.9: при выполнении заданных ограничений на веса ребер время выполнения алгоритма Крускала не превышает 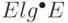с некоторым постоянным коэффициентом (см. "Принципы анализа алгоритмов" ). Напомним, что функция 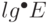равна количеству итераций двоичной логарифмической функции, прежде чем результат станет меньше единицы; это значение меньше 5, если E меньше 2⁶⁵⁵³⁶. То есть такая корректировка делает алгоритм Крускала по сути линейным в большинстве практических ситуаций.

Обычно трудоемкость вычисления MST с помощью алгоритма Крускала даже меньше стоимости обработки всех ребер, поскольку построение завершается задолго до того, как будет просмотрена значительная часть всех ребер (длинного) графа. Этот факт позволяет существенно уменьшить время выполнения во многих практических ситуациях, если вообще не включать в сортировку все ребра, длина которых превышает длину самого длинного ребра MST. Один из самых простых способов достижения этой цели — использование очереди с приоритетами, в реализации которой имеется операция создать с линейным временем выполнения и операция извлечь минимальное с логарифмическим временем.

Например, таких характеристик производительности можно достичь с помощью стандартной реализации пирамидального дерева, используя восходящее построение (см. "Очереди с приоритетами и пирамидальная сортировка" ). При этом в программу 20.8 нужно внести следующие изменения: вызов sort заменить вызовом pq.construct(), чтобы строить пирамидальное дерево за время, пропорциональное E, добавить во внутренний цикл отбор из очереди с приоритетами самых коротких ребер, для которых e = pq.delmin(), и заменить все обращения к a[i] на e.

Эта же идея позволяет получить аналогичные преимущества и в реализации на основе быстрой сортировки. Рассмотрим, что произойдет, если использовать прямую рекурсивную быструю сортировку, где выполняется разбиение по i-му элементу с последующей рекурсивной сортировкой подфайла слева от i и подфайла справа от i. В силу построения алгоритма после завершения первого рекурсивного вызова первые i элементов уже упорядочены (см. программу 9.2). Этот очевидный факт позволяет получить быструю реализацию алгоритма Крускала: если поместить проверку, порождает ли ребро a[i] цикл, между рекурсивными вызовами, то получится алгоритм, который, по построению, после завершения первого рекурсивного вызова уже проверил первые i ребер (в порядке возрастания весов)! Если добавить проверку на прекращение работы после выявления V- 1 ребер MST-дерева, то получается алгоритм, который сортирует лишь столько ребер, сколько их необходимо для вычисления MST-дерева, плюс несколько дополнительных этапов разбиения с участием больших элементов (см. упражнение 20.57). Как и в случае простых реализаций сортировки, этот алгоритм может потребовать квадратичного времени выполнения в худшем случае, однако имеется вероятностная гарантия того, что время выполнения в худшем случае не будет близким к такому пределу. Кроме того, подобно простым реализациям сортировки, эта программа из-за более короткого внутреннего цикла обычно работает быстрее реализации на основе пирамидального дерева.

Если же граф не является связным, то версия алгоритма Крускала на основе частичной сортировки не дает никаких преимуществ, поскольку в этом случае приходится просматривать все ребра графа. Даже в случае связного графа самое длинное ребро может оказаться в MST-дереве, и тогда любая реализация метода Крускала должна просмотреть все ребра. Например, граф может состоять из плотных кластеров вершин, соединенных внутри короткими ребрами, и только одна из вершин кластера соединена с " внешней " вершиной длинным ребром. Несмотря на возможность таких нетипичных вариантов, подход с применением частичной сортировки достоин внимания, поскольку дает существенный выигрыш и не требует больших дополнительных затрат (или вовсе никаких).

Интересны и поучительны и исторические сведения. Крускал предложил свой алгоритм в 1956 г., однако, опять-таки, в течение многих лет не были подробно изучены соответствующие реализации АТД. Поэтому характеристики производительности реализаций, таких как версия программы 20.8 с очередью с приоритетами, не получили надлежащей оценки вплоть до 1970-х годов. Еще один интересный исторический факт: в статье Крускала упоминалась версия алгоритма Прима (см. упражнение 20.59), а Борувка описал в своей статье оба эти подхода. Эффективные реализации метода Крускала для разреженных графов появились раньше реализаций метода Прима для разреженных графов — потому что АТД поиска-объединения (и сортировки) стали применяться раньше, чем АТД очереди с приоритетами. По существу, прогресс в современном состоянии алгоритма Крускала, как и реализации алгоритма Прима, обусловлен главным образом повышением производительности АТД. С другой стороны, возможность применения абстракции поиска-объединения в алгоритме Крускала и возможность применения абстракции очереди с приоритетами в алгоритме Прима стали для многих исследователей основным стимулом для поиска более совершенных реализаций этих АТД.

Упражнения

20.53. Покажите в стиле рис. 20.12 результат вычисления алгоритмом Крускала MST-дерева для сети, определенной в упражнении 20.26.

20.54. Эмпирически определите для различных видов взвешенных графов длину самого длинного ребра MST-дерева и количество ребер графа, длина которых не превосходит длины этого ребра (см. упражнения 20.9—20.14).

20.55. Разработайте реализацию АТД объединения-поиска, в которой операция найти выполняется за постоянное время, а операция объединить — за время, пропорциональное lgV.

20.56. Эмпирически сравните для различных видов взвешенных графов реализацию АТД из упражнения 20.55 со взвешенным объединением-поиском с делением пополам (программа 1.4), когда алгоритм Крускала является клиентской программой (см. упражнения 20.9—20.14). Выделите затраты на сортировку ребер отдельно, чтобы можно было изучать влияние замены на общие затраты и на часть расходов, связанных с АТД объединения-поиска.

20.57. Разработайте реализацию на основе описанной в тексте идеи: интеграции алгоритма Крускала с быстрой сортировкой, чтобы проверять каждое ребро на принадлежность MST-дереву сразу после проверки всех ребер с меньшими весами.

20.58. Добавьте в алгоритм Крускала реализации двух функций АТД, которые заполняют вектор, индексированный именами вершин, который поставляется клиентской программой. Этот вектор разбивает вершины на к таких кластеров, что ни одно ребро с длиной, большей d, не соединяет две вершины из различных кластеров. Первая функция принимает в качестве аргумента к и возвращает d, а вторая принимает в качестве аргумента d и возвращает к. Протестируйте полученную программу для различных к и d на случайных евклидовых графах с соседними связями и на решетчатых графах (см. упражнения 20.17 и 20.19) различных размеров.

20.59. Разработайте реализацию алгоритма Прима, основанного на предварительной сортировке ребер.

20.60. Напишите клиентскую программу, которая выполняет динамическую графическую анимацию алгоритма Крускала (см. упражнение 20.52). Проверьте полученную программу на случайных евклидовых графах с соседними связями и на решетчатых графах (см. упражнения 20.17 и 20.19) , используя столько точек, сколько можно обработать за приемлемое время.