Проект "Компилятор формул"
Грамматики языка правильных арифметических формул
Разобравшись с языком программ стекового калькулятора, на который мы
будем осуществлять перевод, попробуем теперь формально описать язык правильных
арифметических формул, с которого этот перевод будет производиться.
Для простоты ограничимся случаем, когда в формулах фигурируют только
односимвольные переменные, запрещено использование унарных операций, а
символ  , обозначающий умножение, не может быть опущен.
, обозначающий умножение, не может быть опущен.
В качестве алфавита  возьмем то же самое множество, что
и раньше,
состоящее из двух
круглых скобок (открывающей и закрывающей), четырех знаков
арифметических операций (
возьмем то же самое множество, что
и раньше,
состоящее из двух
круглых скобок (открывающей и закрывающей), четырех знаков
арифметических операций ( 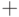 ,
, 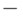 ,
,  и
и 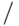 ) и 26-и
идентификаторов от
) и 26-и
идентификаторов от  до
до  , которыми будут
обозначаться произвольные
целые числа:
, которыми будут
обозначаться произвольные
целые числа:

В качестве метаалфавита рассмотрим множество из трех нетерминалов:
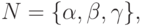
 будет обозначать формулу,
будет обозначать формулу,  — имя переменной,
а
— имя переменной,
а  — арифметическую операцию.
— арифметическую операцию.Множество правил  грамматики
грамматики 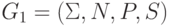 зададим так:
зададим так:
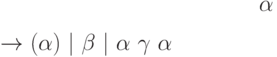
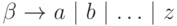
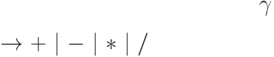
Стартовым метасимволом этой грамматики является нетерминал  , а примером
вывода в ней может служить следующий вывод формулы
, а примером
вывода в ней может служить следующий вывод формулы  :
:

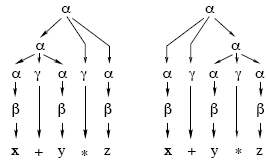
Для формулы 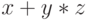 существует два существенно различных
множества
эквивалентных между собой цепочек вывода, каждому из которых соответствует
свое дерево вывода. Эти деревья изображены на рис. 12.2
и отличаются друг от друга порядком появления в формуле операций
существует два существенно различных
множества
эквивалентных между собой цепочек вывода, каждому из которых соответствует
свое дерево вывода. Эти деревья изображены на рис. 12.2
и отличаются друг от друга порядком появления в формуле операций 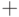 и
и  .
Хотя в результате различных выводов получается одна и та же формула, вычисления по ним дадут различные результаты. В одном случае
выражение
.
Хотя в результате различных выводов получается одна и та же формула, вычисления по ним дадут различные результаты. В одном случае
выражение 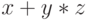 трактуется как
трактуется как 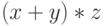 , а в другом
— как
, а в другом
— как 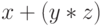 .
.
Таким образом, грамматика 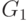 хотя и задает язык правильных
арифметических
формул, не отражает старшинства операций (приоритетов). Тот же самый язык
может быть задан с помощью иной грамматики
хотя и задает язык правильных
арифметических
формул, не отражает старшинства операций (приоритетов). Тот же самый язык
может быть задан с помощью иной грамматики 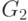 , в которой этот
недостаток
устранен.
, в которой этот
недостаток
устранен.
Множество нетерминалов для этой грамматики будет состоять из четырех
метасимволов —  ,
,  ,
,  и
и  , обозначающих соответственно формулу, терм, множитель и имя переменной. Множество
правил
, обозначающих соответственно формулу, терм, множитель и имя переменной. Множество
правил  грамматики
грамматики 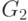 зададим так:
зададим так:
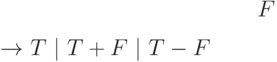
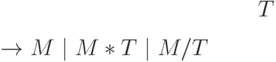

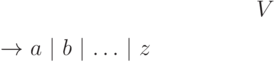
По ряду причин чуть позже нам понадобятся другие грамматики рассматриваемого языка.
Грамматика 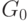 отличается от только что рассмотренной
отличается от только что рассмотренной 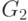 порядком
следования нетерминалов в правой части первых двух правил:
порядком
следования нетерминалов в правой части первых двух правил:
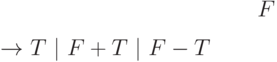
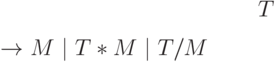

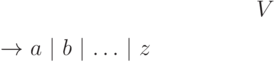
Важные свойства именно этой грамматики определяют ее обозначение. Именно
грамматика 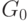 языка правильных арифметических формул будет
использоваться
в целом ряде последующих учебных курсов.
языка правильных арифметических формул будет
использоваться
в целом ряде последующих учебных курсов.
Еще один вариант грамматики (назовем ее  ) таков:
) таков:
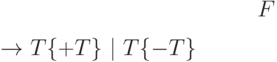
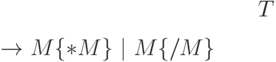

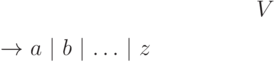
Фигурные скобки в этой записи означают повторение фрагмента, в них
стоящего, нуль или более раз. Таким образом, первое правило этой грамматики
означает,
что метасимвол  может быть преобразован в
может быть преобразован в  ,
,  ,
,  ,
, 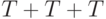 ,
, 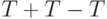 ,
, 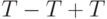 ,
, 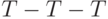 и т.д.
и т.д.
Докажите самостоятельно, что все приведенные выше грамматики задают один и тот же язык правильных арифметических формул.