|
По первому тесту выполнил дважды задания. Результат получается правильный (проверял калькулятором). Пишет, что "Задание не проверено" и предлагает повторить. |
Обработка матриц в Паскале
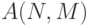 найти строки, в которых находится максимальное из простых чисел. Элементы в них упорядочить по возрастанию. Если в матрице нет простых чисел, то оставить её без изменений.
найти строки, в которых находится максимальное из простых чисел. Элементы в них упорядочить по возрастанию. Если в матрице нет простых чисел, то оставить её без изменений.Перед решением задачи отметим её некоторые особенности6Авторы рекомендуют читателям внимательно изучить этот пример, в нём сконцентрированы практически все основные моменты, рассмотренные нами до сих пор.. В матрице может не быть простых чисел, максимальных значений может быть несколько, и при этом некоторые из них могут находиться в одной строке.
При решении задачи нам понадобятся следующие подпрограммы:
- Функция Prostoe, которая проверяет, является ли число P типа word простым. Она возвращает значение true, если число P — простое, и false — в противном случае. Заголовок функции имеет вид
function Prostoe (P : word ) : Boolean;
- Процедура Udal, которая из массива чисел X удаляет значения, встречающиеся более одного раза. У процедуры два параметра: массив X и его размер N, оба — параметры-переменные. Заголовок процедуры имеет вид:
Перед описанием процедуры следует описать тип данных massiv (например, massiv = array [1..200] of word). Блок-схема процедуры Udal представлена на рис. 6.31. Удаление повторяющихся элементов происходит следующим образом. Просматриваются все элементы, начиная спервого, i-й элемент сравнивается со всеми последующими. Если, то встретился повторяющийся элемент, и мы удаляем из массива элемент с номером j. Алгоритм удаления был подробно рассмотрен в главе 5.
procedure Udal ( var X: massiv; var N: word );
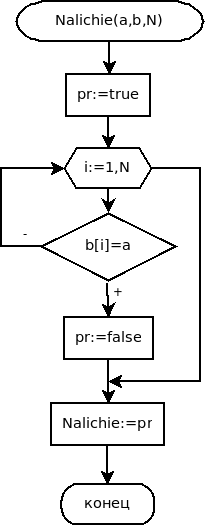
- Функция Nalichie возвращает true, если число a присутствует в массиве b, и false — в противном случае. Заголовок процедуры имеет вид:
Блок-схема функции представлена на рис. 6.32.
function Nalichie ( a : word; b : massiv; N: word );
- Процедура Vozr упорядочения массива х по возрастанию. Алгоритмы упорядочения рассматривались в главе 5. Здесь авторами использовался алгоритм сортировки методом пузырька. У процедуры Vozr два параметра: массив х (параметр-переменная) и его размер N (параметр-значение). Заголовок процедуры имеет вид:
procedure Vozr ( var x : massiv; N: word );
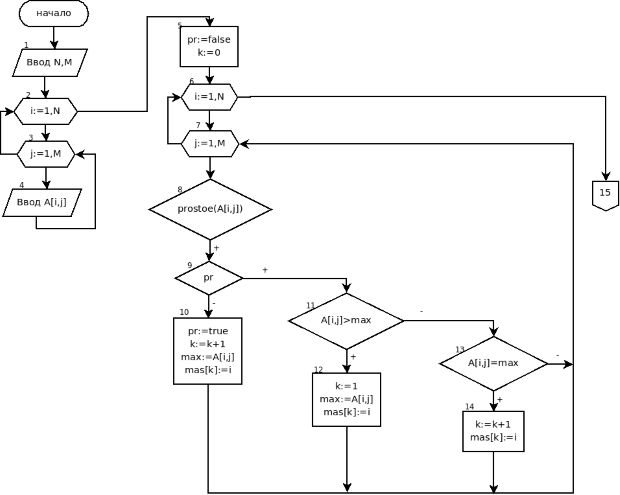
Рассмотрим более подробно алгоритм решения задачи 6.11, который приведён на рис. 6.33—6.34.
После ввода матрицы (блоки 1—4) предполагаем, что простых чисел нет. В логическую переменную Pr записываем false, как только встретится простое число, в переменную Pr запишем true. Количество максимальных значений среди простых чисел равно 0 (k:=0) (блок 5).
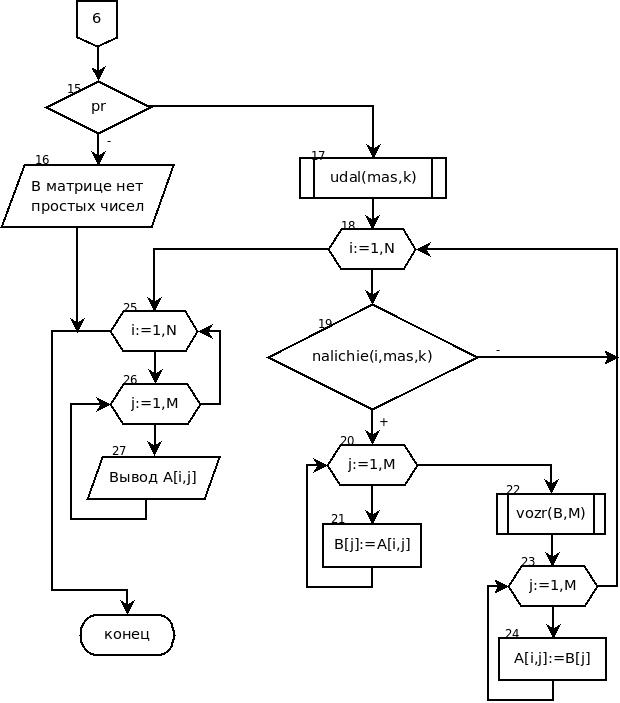
Для проверки, является ли простым числом каждый элемент матрицы, обращаемся к функции Prostoe. Если число простое (блок 8), проверяем, первое ли это простое число в матрице (блок 9). Если это первое простое число, то переписываем его в переменную max, в переменную k записываем число 1 (количество максимумов равно 1), номер строки, в которой находится максимум, записываем в массив mas под номером k7В массиве mas будут храниться номера строк, в которых находится максимум.. В связи с тем, что в матрице есть простые числа, в переменную Pr записываем true (блок 10). Если это не первое простое число, сравниваем A[i,j] с переменной max. Если A[i,j]>max (блок 11), то в переменную max запишем A[i,j], в переменную k запишем 1 (есть один максимум), в mas[k] записываем i — номер строки, где находится максимальный элемент (блок 12). Если A[i,j]=max (блок 13), то встретилось число, равное переменной max. В этом случае значение k увеличиваем на 1 и в mas[k] записываем номер строки, где находится элемент, равный max. В результате двойного цикла обработки всех элементов матрицы (блоки 6—14) в переменной max будет храниться максимальное из простых чисел, в переменной k — количество максимумов, в массиве mas из k элементов будут храниться номера строк, где находятся максимальные значение среди простых чисел матрицы. В переменной Pr хранится true, если в матрице есть простые числа, false — в противном случае. Если в матрице нет простых чисел (блок 15), выводим соответствующее сообщение (блок 16), в противном случае с помощью процедуры Udal (блок 17) удаляем из массива mas элементы, встречающиеся более одного раза8Если некоторые максимальные элементы находятся в одной строке, то в массиве mas есть повторяющиеся элементы.. Затем просматриваем все строки матрицы (цикл начинается блоком 18). Если номер этой строки присутствует в массиве mas (блок 19), то переписываем текущую строку матрицы в массив b (блоки 20—21) и обращаемся к процедуре упорядочения массива по возрастанию Vozr (блок 22). Упорядоченный массив b переписываем в i-ю строку матрицы А (блоки 23—24). На последнем этапе выводим на экран матрицу А после преобразования (блоки 25—27).
Ниже приведён листинг всей программы с подробными комментариями.
{Тип данных massiv будет использоваться при описании процедур.}
type
massiv=array [ 1.. 200 ] of word;
{Функция prostoe проверяет, является ли число N простым (true) или нет}
{(false).}
function prostoe (N: word ) : boolean;
var pr : boolean; i : word;
begin
if N>0 then
begin
{Предполагаем, что число N - простое (pr=true).}
pr := true;
{Проверяем, делится ли число N на какое либо из чисел от 2 до N/2.}
for i :=2 to n div 2 do
{Если встречается число i, на которое делится N, то}
if N mod i =0 then
begin
{число N не является простым (pr=false) и}
pr := false;
{выходим из цикла.}
break;
end
end
else pr := false;
{Имени функции присваиваем значение переменной pr.}
prostoe := pr;
end;
{Процедура udal удаляет из массива x элементы, которые встречаются}
{более одного раза. Х, N являются параметрами-переменными, так как эти}
{значения возвращаются в головную программу при вызове процедуры udal.}
procedure udal ( var x : massiv; var n : word );
var i, j,m: word;
begin
i : = 1;
{Просматриваем все элементы, начиная с первого i=1,2,...,N;i-й элемент}
{сравниваем с последующими j=i+1,i+2,...,n.}
while ( i<=n ) do
begin
j := i +1;
while ( j<=N) do
{Если x[i] равно x[j], то встретился повторяющийся элемент -}
if x [ i ]=x [ j ] then
begin
{удаляем его (x[j]) из массива.}
for m:= j to N _1 do
x [m] : = x [m+ 1 ];
{После удаления элемента количество элементов уменьшаем на 1, при этом}
{не переходим к следующему элементу, так как после удаления под j-м}
{номером находится уже другой элемент.}
N:=N-1;
End
{Если x[i] не равно x[j], то переходим к следующему элементу.}
else j := j +1;
i := i +1;
end;
end;
{Функция nalichie возвращает true, если число a встречается в массиве}
{b, false - в противном случае.}
function nalichie ( a : word; b : massiv; n : word ) : boolean;
var
pr : boolean;
i : word;
begin
{Предполагаем, что в массиве b не встречается значение a - pr=false}
pr := false;
{Перебираем все элементы массива.}
for i :=1 to N do
{Если очередной элемент массива b равен значению a, то в pr записываем}
{true}
if b [ i ]=a then
begin
pr := true;
{и выходим из цикла.}
break
end;
{Имени функции присваиваем значение переменной pr.}
nalichie := pr
end;
{Процедура vozr упорядочивает массив x по возрастанию.}
procedure vozr ( var x : massiv; n : word );
{X является параметром-переменной, именно массив и возвращается в}
{головную программу при вызове процедуры vozr.}
var i, j, b : word;
begin
for i :=1 to N -1 do
for j :=1 to N -i do
if x [ j ]>x [ j +1] then
begin
b:=x [ j ];
x [ j ] : = x [ j + 1 ];
x [ j +1]:=b;
end
end;
//Начинается основная программа.
var
N, M, i, j, k, max : word;
A: array [ 1.. 20, 1.. 20 ] of word;
pr, L : boolean;
mas, b : massiv;
begin
{Вводим элементы матрицы А.}
write ( ’N= ’ ); readln (N);
write ( ’M= ’ ); readln (M);
writeln ( ’ Matrica A ’ );
for i :=1 to N do
for j :=1 to M do
read (A[ i, j ] );
{Предполагаем, что в матрице нет простых чисел.}
Pr:= false;
{Количество элементов, равных максимальному, равно 0.}
k : = 0;
{Перебираем все элементы в матрице.}
for i :=1 to N do
for j :=1 to M do
begin
{Обращаемся к функции, которая проверяет, является ли число A[i,j]}
{простым.}
L:= Prostoe (A[ i, j ] );
{Если число простое, и}
if L then
{если простое число встретилось первый раз,}
if not Pr then
begin
{записывем в pr true,}
Pr:= true;
{увеличиваем количество максимумов на 1, можно было просто написать}
{k:=1.}
k:=k+1;
{Это число записываем в переменную max. Это первое простое число, и}
{предполагаем, что оно максимальное.}
max:=A[ i, j ];
{В mas[k] записываем номер строки, где хранится число A[i,j].}
mas [ k ] : = i
end
else
{Если A[i,j] - не первое простое число, то сравниваем max и текущее}
{простое значение матрицы А.}
if A[ i, j ]>max then
{Если A[I,j]> max, то}
begin
{количество максимумов равно 1, т. к. встретился наибольший в данный}
{момент элемент.}
k : = 1;
{В переменную max записываем A[i,j],}
max:=A[ i, j ];
{в mas[k] записываем номер строки, где хранится число A[i,j]}
mas [ k ] : = i
end
else
{Если A[i,j]=max (встретился элемент, равный максимуму), то}
if A[ i, j ]=max then
begin
{количество максимумов увеличиваем на 1,}
k:=k+1;
{в mas[k] записываем номер строки, где хранится число A[i,j].}
mas [ k ] : = i
end
end;
{Если в pr осталось значение false,то выводим сообщение, что в матрице}
{нет простых чисел,}
if not Pr then writeln ( ’В матрице A нет простых чисел ’ )
else
begin
{иначе удаляем из массива mas номера строк, где хранятся максимумы,}
{повторяющиеся элементы.}
Udal ( mas, k );
{Перебираем все строки матрицы.}
for i :=1 to N do
begin
L:= Nalichie ( i, mas, k );
{Если номер строки присутствует в массиве mas,}
if L then
begin
{то переписываем строку в массив b,}
for j :=1 to M do
b [ j ] : =A[ i, j ];
{упорядочиваем массив b по возрастанию.}
Vozr ( b,M);
{Упорядоченный массив записываем на место i-й строки матрицы A.}
for j :=1 to M do
A[ i, j ] : = b [ j ];
end
end;
writeln ( ’Преобразованная матрица A ’ );
for i :=1 to N do
begin
for j :=1 to M do
write (A[ i, j ], ’ ’ );
writeln;
end
end
end.
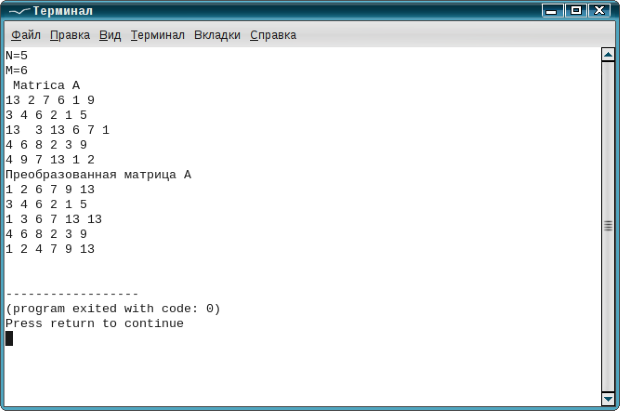
Результаты работы программы приведены на рис. 6.35.
Авторы рекомендуют читателю по рассмотренным алгоритмам и консольным приложениям задач 6.7—6.11 разработать визуальные приложения, аналогичные тем, которые были разработаны для задач 6.2 и 6.6.
В завершении этой главы рассмотрим "динамические матрицы".
6.3 Динамические матрицы
Понятие динамического массива можно распространить и на матрицы. Динамическая матрица представляет собой массив указателей, каждый из которых адресует одну строку (или один столбец).
Рассмотрим описание динамической матрицы. Пусть есть типы данных massiv и указатель на него din_massiv.
type massiv=array [ 1.. 1000 ] of real;
din_massiv=^massiv;
Динамическая матрица X будет представлять собой массив указателей.
var X: array [ 1.. 100 ] of din_massiv;
Работать с матрицей надо следующим образом:
- Определить её размеры (пусть N — число строк, M — число столбцов).
- Выделить память под матрицу.
for i :=1 to N do
getmem(X[ i ],M * sizeof ( real ) );
Каждый элемент статического массива X[i] — указатель на динамический массив, состоящий из M элементов типа real. В статическом массиве Х находится N указателей.
- Для обращения к элементу динамической матрицы, расположенному в i-й строке и j-м столбце, следует использовать конструкцию языка Турбо Паскаль X[i]^[j].
- После завершения работы с матрицей необходимо освободить память.
for i :=1 to N do
freemem ( b [ i ],M * sizeof ( real ) );
Рассмотрим работу с динамической матрицей на следующем примере.
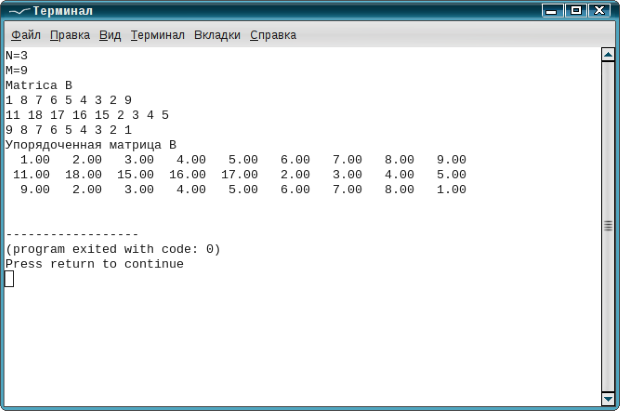
ЗАДАЧА 6.12. В каждой строке матрицы вещественных чисел B(N, M ) упорядочить по возрастанию элементы, расположенные между максимальным и минимальным значениями.
Алгоритмы упорядочения рассматривались в главе 5, основные принципы работы с матрицами — в предыдущих параграфах текущей главы, поэтому в комментариях к тексту программы основное внимание уделено особенностям работы с динамическими матрицами.
{Описываем тип данных massiv как массив 1000 вещественных чисел.}
type massiv=array [ 1.. 1000 ] of real;
{Указатель на массив.}
din_massiv=^massiv;
{Тип данных matrica - статический массив указателей, каждый элемент}
{которого является адресом массива вещественных чисел.}
matrica=array [ 1.. 100 ] of din_massiv;
var
Nmax, Nmin, i, j, n,m, k : word;
{Описана динамическая матрица b.}
b : matrica;
a, max, min : real;
begin
{Вводим число строк N и число столбцов M.}
write ( ’N= ’ ); readln (N);
write ( ’M= ’ ); readln (M);
{Выделяем память под матрицу вещественных чисел размером N на M.}
for i :=1 to N do
getmem( b [ i ],M * sizeof ( real ) );
{ Вводим Матрицу B. }
writeln ( ’ Matrica B ’ );
for i :=1 to N do
for j :=1 to M do
read ( b [ i ] ^ [ j ] );
{В каждой строке находим максимальный, минимальный элементы и их номера}
{и элементы, расположенные между ними, упорядочиваем "методом}
{пузырька".}
for i :=1 to N do
begin
{Поиск минимального, максимального элемента в i-й строке матрицы и их}
{номеров.}
max:=b [ i ] ^ [ 1 ];
Nmax: = 1;
min:=b [ i ] ^ [ 1 ];
Nmin : = 1;
for j :=2 to M do
begin
if b [ i ] ^ [ j ]>max then
begin
max:=b [ i ] ^ [ j ];
nmax:= j
end;
if b [ i ] ^ [ j ]<min then
begin
min:=b [ i ] ^ [ j ];
nmin:= j
end;
end;
{Если минимальный элемент расположен позже максимального, nmin и nmax}
{меняем местами.}
if nmax<nmin then
begin
j :=nmax;
nmax:=nmin;
nmin:= j;
end;
{В i-той строке упорядочиваем элементы, расположенные между nmin и}
{nmax, "методом пузырька".}
j : = 1;
while nmax-1 - j>=nmin+1 do
begin
for k:=nmin+1 to nmax-1 - j do
if b [ i ] ^ [ k]>b [ i ] ^ [ k+1] then
begin
a:=b [ i ] ^ [ k ];
b [ i ] ^ [ k ] : = b [ i ] ^ [ k + 1 ];
b [ i ] ^ [ k+1]:= a;
end;
j := j +1;
end;
end;
{ Выводим преобразованную матрицу. }
writeln ( ’Упорядоченная матрица B ’ );
for i :=1 to N do
begin
for j :=1 to M do
write ( b [ i ] ^ [ j ] : 6 : 2, ’ ’ );
writeln
end;
{ Освобождаем память. }
for i :=1 to N do
freemem ( b [ i ],M * sizeof ( real ) );
end.
Результаты работы программы представлены на рис. 6.36.
Динамическая матрица может быть достаточно большой, фактически её размер ограничен только объемом свободной памяти.
В заключении главы приведём задачи для самостоятельного решения.