|
По первому тесту выполнил дважды задания. Результат получается правильный (проверял калькулятором). Пишет, что "Задание не проверено" и предлагает повторить. |
Использование языка Free Pascal для обработки массивов
5.5 Вычисление суммы и произведения элементов массива
Нахождение суммы и произведения элементов массива аналогичны алгоритмам нахождения суммы и произведения элементов последовательности.
Дан массив X, состоящий из n элементов. Найти сумму элементов этого массива. Переменной S присваивается значение, равное нулю, затем последовательно суммируются элементы массива X. Блок-схема алгоритма расчёта суммы приведена на рис. 5.19.
Соответствующий алгоритму фрагмент программы будет иметь вид:
s : = 0; for i :=1 to n do s := s+x [ i ]; writeln ( ’ s= ’, s : 7 : 3 );
Найдём произведение элементов массива X. Решение задачи сводится к тому, что значение переменной Р, в которую предварительно была записана единица, последовательно умножается на значение i-го элемента массива. Блок-схема алгоритма приведена на рис. 5.20.
Соответствующий фрагмент программы будет иметь вид:
p : = 1; for i :=1 to n do p:=p * x [ i ]; writeln ( ’P= ’,P : 7 : 3 );
5.6 Поиск максимального элемента в массиве и его номера
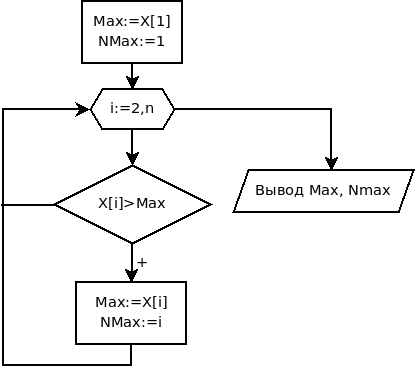
Рассмотрим задачу поиска максимального элемента (Max) и его номера (Nmax) в массиве X, состоящем из n элементов.
Алгоритм решения задачи следующий. Предположим, что первый элемент массива является максимальным, и запишем его в переменную Max, а в Nmax — его номер (число 1). Затем все элементы, начиная со второго, сравниваем в цикле с максимальным. Если текущий элемент массива оказывается больше максимального, то записываем его в переменную Max, а в переменную Nmax — текущее значение индекса i. Процесс определения максимального элемента в массиве изображен при помощи блок-схемы на рис. 5.21.
Соответствующий фрагмент программы имеет вид:
Max:=X [ 1 ]; Nmax: = 1; for i :=2 to n do if X[ i ]>Max then begin Max:=X[ i ]; Nmax:= i; end; write ( ’ Max= ’,Max : 1 : 3, ’ Nmax= ’,Nmax );
Алгоритм поиска минимального элемента в массиве будет отличаться от приведённого выше лишь тем, что в условном блоке и, соответственно, в конструкции if текста программы знак поменяется с > на <.
5.7 Сортировка элементов в массиве
Сортировка представляет собой процесс упорядочения элементов в массиве в порядке возрастания или убывания их значений. Например, массив  из
из  элементов будет отсортирован в порядке возрастания значений его элементов, если
элементов будет отсортирован в порядке возрастания значений его элементов, если
![X[1] \le X[2] \le \ldots \le X[n],](/sites/default/files/tex_cache/3e493570b7d969fb645212cd831d26ac.png)
и в порядке убывания, если
![X[1] \ge X[2] \ge \ldots \ge X[n].](/sites/default/files/tex_cache/24bb051cdb361d1640b7ca7226b7f3fa.png)
Многие алгоритмы сортировки основаны на том факте, что переставлять два элемента надо таким образом, чтобы после перестановки они были правильно расположены друг относительно друга. При сортировке по возрастанию после перестановки элемент с меньшим индексом должен быть не больше элемента с большим индексом2При сортировке по убыванию после перестановки элемент с меньшим индексом должен быть не меньше элемента с большим индексом.. Рассмотрим некоторые из алгоритмов.
5.7.1 Сортировка методом "пузырька"
Наиболее известным методом сортировки является сортировка массивов пузырьковым методом. Её популярность объясняется запоминающимся названием3Название алгоритма объясняется его сходством с процессом движения пузырьков в резервуаре с водой, когда каждый пузырёк находит свой собственный уровень. и простотой алгоритма. Сортировкаметодом "пузырька" основана на выполнении в цикле операций сравнения и при необходимости обмена соседних элементов. Рассмотрим алгоритм пузырьковой сортировки на примере сортировки по возрастанию более подробно.
Сравним первый элемент массива со вторым, если первый окажется больше второго, то поменяем их местами. Затем сравним второй с третьим, и если второй окажется больше третьего, то поменяем и их. Далее сравниваем третий и четвёртый, и если третий большего четвёртого, их также меняем местами. После трёх этих сравнений самым большим элементом станет элемент с номером 4. Если продолжить сравнение соседних элементов: сравнить четвертый с пятым, пятый с шестым и т. д. до сравнения 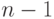 -го и n-го элементов, то в результате этих действий самый большой элемент станет на последнее (
-го и n-го элементов, то в результате этих действий самый большой элемент станет на последнее ( -е) место.
-е) место.
| Номер элемента | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Исходный массив | 7 | 3 | 5 | 4 | 2 |
| Первый просмотр | 3 | 5 | 4 | 2 | 7 |
| Второй просмотр | 3 | 4 | 2 | 5 | 7 |
| Третий просмотр | 3 | 2 | 4 | 5 | 7 |
| Четвёртый просмотр | 2 | 3 | 4 | 5 | 7 |
Теперь повторим данный алгоритм сначала с 1-го до  элемента (последний
элемента (последний  -й элемент, рассматривать не будем, так как он уже занял свое место). После проведения данной операции самый большой элемент оставшейся части массива станет на своё (
-й элемент, рассматривать не будем, так как он уже занял свое место). После проведения данной операции самый большой элемент оставшейся части массива станет на своё (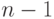 -е) место. Так повторяем до тех пор, пока не упорядочим весь массив.
-е) место. Так повторяем до тех пор, пока не упорядочим весь массив.
В табл. 5.8 подробно показан процесс упорядочения элементов в массиве.
Нетрудно заметить, что для преобразования массива, состоящего из  элементов, необходимо просмотреть его
элементов, необходимо просмотреть его 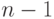 раз, каждый раз уменьшая диапазон просмотра на один элемент. Блок-схема описанного алгоритма приведена на рис. 5.22. Для обмена двух элементов в массиве (блок 4) используется буферная переменная
раз, каждый раз уменьшая диапазон просмотра на один элемент. Блок-схема описанного алгоритма приведена на рис. 5.22. Для обмена двух элементов в массиве (блок 4) используется буферная переменная  , в которой временно хранится значение элемента, подлежащего замене.
, в которой временно хранится значение элемента, подлежащего замене.
Ниже приведён текст консольного приложения, предназначенного для упорядочения массива по возрастанию методом пузырька.
program upor_massiv;
var i, j, n : byte;
X: array [ 1.. 100 ] of real;
b : real;
begin
writeln ( ’введите размер массива ’ );
readln ( n );
for i :=1 to n do
begin
write ( ’X[ ’, i, ’ ]= ’ );
readln (X[ i ] );
end;
writeln ( ’массив X ’ );
for i :=1 to n do write ( x [ i ] : 5 : 2, ’ ’ );
writeln;
for j :=1 to n-1 do
for i :=1 to n-j do
if X[ i ] > X[ i +1] then
{Если текущий элемент больше следующего, то}
begin {поменять их местами.}
b:=X[ i ]; {Сохранить значение текущего элемента.}
X[ i ] : =X[ i + 1 ]; {Заменить текущий элемент следующим.}
X[ i +1]:=b; {Заменить следующий элемент переменной b.}
end;
writeln ( ’упорядоченный массив ’ );
for i :=1 to n do
write (X[ i ] : 5 : 2, ’ ’ );
writeln;
end.
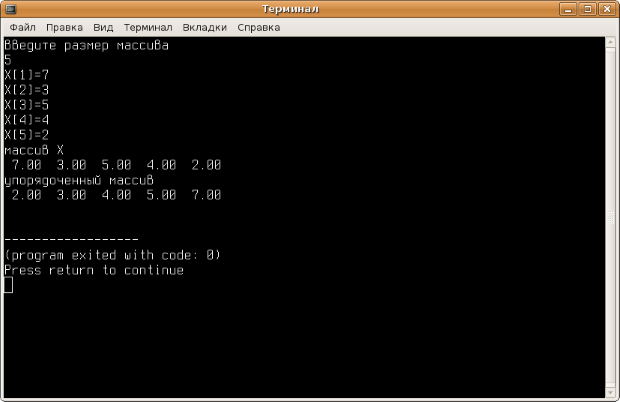
На рис. 5.23 приведены результаты работы этой программы.
Для упорядочения элементов в массиве по убыванию их значений необходимо при сравнении элементов массива заменить знак > на < (см. блок 3 на рис. 5.22).
Рассмотрим следующий алгоритм сортировки.
5.7.2 Сортировка выбором
Для сортировки элементов массива по возрастанию (по убыванию) можно воспользоваться алгоритмом сортировки выбора максимального (минимального) элемента. Алгоритм выбором приведён в виде блок-схемы на рис. 5.24.
Найдём в массиве самый большой элемент (блоки 2—5) и поменяем его местами с последним элементом (блок 6). После этого максимальный элемент встанет на своё место. Теперь надо повторять эти действия (блоки 2—6), уменьшив количество просматриваемых элементов на единицу (блок 7) до тех пор, пока количество рассматриваемых элементов не станет равным одному (блок 8). В связи с тем, что мы на каждом шаге уменьшаем количество элементов на 1, то, чтобы не потерять размер массива (N), необходимо в начале алгоритма переписать N в переменную K (блок 1) и уменьшать уже значение K.
При упорядочении массива по убыванию необходимо перемещать минимальный элемент. Для этого в алгоритме (рис. 5.24) в блоке 4 достаточно поменять знак > на знак <.
Ниже приведён фрагмент программы упорядочения массива по возрастанию, используя сортировку выбором максимального элемента.
k:=n; repeat max:=x [ 1 ]; nom: = 1; for i :=2 to k do if max < X[ i ] then begin max:=X[ i ]; nom:= i; end; b:=x [ nom ]; x [ nom] : = x [ k ]; x [ k ] : = b; k:=k -1; until k=1;
Следующим важным алгоритмом обработки массивов является алгоритм удаления элемента из массива.