|
По первому тесту выполнил дважды задания. Результат получается правильный (проверял калькулятором). Пишет, что "Задание не проверено" и предлагает повторить. |
Общие сведения о языке программирования Free Pascal
2.5 Операции и выражения
Выражение задаёт порядок выполнения действий над данными и состоит из операндов (констант, переменных, обращений к функциям), круглых скобок и знаков операций, например a+b*sin(cos(x)). В табл. 2.4 представлены основные операции языка программирования Free Pascal.
| Операция | Действие | Тип операндов | Тип результата |
|---|---|---|---|
| + | сложение | целый/вещественный | целый/вещественный |
| + | сцепление строк | строковый | строковый |
| – | вычитание | целый/вещественный | целый/вещественный |
| * | умножение | целый/вещественный | целый/вещественный |
| / | деление | целый/вещественный | вещественный |
| div | целочисленное деление | целый | целый |
| mod | остаток от деления | целый | целый |
| not | арифметическое/логическое | отрицание | целый/логический целый/логический |
| and | арифметическое/логическое И | целый/логический | целый/логический |
| or | арифметическое/логическое ИЛИ | целый/логический | целый/логический |
| xor | арифметическое/логическое исключающее ИЛИ | целый/логический | целый/логический |
| shl | сдвиг влево | целый | целый |
| shr | сдвиг вправо | целый | целый |
| in | вхождение в множество | множество | логический |
| < | меньше | не структурированный | логический |
| > | больше | не структурированный | логический |
| <= | меньше или равно | не структурированный | логический |
| >= | больше или равно | не структурированный | логический |
| = | равно | не структурированный | логический |
| <> | не равно | не структурированный | логический |
В сложных выражениях порядок, в котором выполняются операции, соответствует приоритету операций. В языке Free Pascal приняты следующие приоритеты:
- not.
- *, /, div, mod, and, shl, shr.
- +, –, or, xor.
- =, <>, >, <, >=, <=.
Использование скобок в выражениях позволяет менять порядок вычислений.
Перейдём к подробному рассмотрению основных операций языка.
2.5.1 Арифметические операции
Операции +, –, *, / относят к арифметическим операциям. Их назначение понятно и не требует дополнительных пояснений.
Операции целочисленной арифметики (применяются только к целочисленным операндам):
- div — целочисленное деление (возвращает целую часть частного, дробная часть отбрасывается), например, 17 div 10 = 1;
- mod — остаток от деления, например, 17 mod 10 = 7.
К операциям битовой арифметики относятся следующие операции: and, or, xor, not, shl, shr. В операциях битовой арифметики действия происходят над двоичным представлением целых чисел.
Арифметическое И (and)5Конъюнкция.. Оба операнда переводятся в двоичную систему, затем над ними происходит логическое поразрядное умножение операндов по следующим правилам:
1 and 1 = 1
1 and 0 = 0
0 and 1 = 0
0 and 0 = 0
Например, если 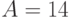 и
и  , то их двоичное представление —
, то их двоичное представление —  и
и  . В результате логического умножения A and B получим 0000000000001000 или 8 в десятичной системе счисления (рис. 2.1). Таким образом,
. В результате логического умножения A and B получим 0000000000001000 или 8 в десятичной системе счисления (рис. 2.1). Таким образом,  .
.
Арифметическое ИЛИ (or)6Дизъюнкция.. Здесь оба операнда также переводятся в двоичную систему, после чего над ними происходит логическое поразрядное сложение операндов по следующим правилам:
1 or 1 = 1
1 or 0 = 1
0 or 1 = 1
0 or 0 = 0
Например, результат логического сложения чисел 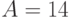 и
и  будет равен A or B = 30 (рис. 2.2).
будет равен A or B = 30 (рис. 2.2).
Арифметическое исключающее ИЛИ (xor). Оба операнда переводятся в двоичную систему, после чего над ними происходит логическая поразрядная операция xor по следующим правилам:
1 xor 1 = 0
1 xor 0 = 1
0 xor 1 = 1
0 xor 0 = 0
Арифметическое отрицание (not). Эта операция выполняется над одним операндом. Применение операции not вызывает побитную инверсию7Побитная инверсия — замена в двоичном представлении числа нулей единицами, единиц — нулями. двоичного представления числа (рис. 2.3).
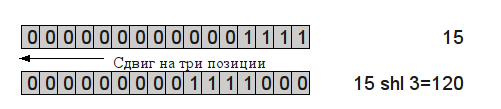
Сдвиг влево (M shl L). Двоичное представление числа  сдвигается влево на
сдвигается влево на  позиций. Рассмотрим операцию 15 shl 3. Число 15 в двоичной системе имеет вид 1111. При сдвиге его на 3 позиции влево получим 1111000. В десятичной системе это двоичное число равно 120. Итак, 15 shl 3 = 120 (рис. 2.4).
позиций. Рассмотрим операцию 15 shl 3. Число 15 в двоичной системе имеет вид 1111. При сдвиге его на 3 позиции влево получим 1111000. В десятичной системе это двоичное число равно 120. Итак, 15 shl 3 = 120 (рис. 2.4).
Заметим, что сдвиг на один разряд влево соответствует умножению на два, на два разряда — умножению на четыре, на три — умножению на восемь. Таким образом, операция M shl L эквивалентна умножению числа  на 2 в степени
на 2 в степени  .
.
Сдвиг вправо (M shr L). В этом случае двоичное представление числа  сдвигается вправо на
сдвигается вправо на  позиций, что эквивалентно целочисленному делению числа
позиций, что эквивалентно целочисленному делению числа  на 2 в степени
на 2 в степени  . Например, 15 shr 1 = 7 (рис. 2.5), 15 shr 3 = 2.
. Например, 15 shr 1 = 7 (рис. 2.5), 15 shr 3 = 2.