Числовые характеристики распределений
Свойства дисперсии
Свойства дисперсии следуют из соответствующих свойств математического ожидания. Заметим, что из существования второго момента следует существование математического ожидания случайной величины и конечность дисперсии. Во всех свойствах ниже предполагается существование вторых моментов случайных величин.
(D1) Дисперсия может быть вычислена по формуле:  .
.
Доказательство. Положим для удобства 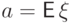 . Тогда
. Тогда
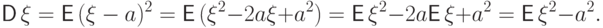
(D2)
При умножении случайной величины на постоянную  дисперсия увеличивается в
дисперсия увеличивается в 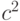 раз:
раз:  .
.
(D3) Дисперсия всегда неотрицательна:  .
Дисперсия
обращается в нуль лишь для вырожденного распределения:
если
.
Дисперсия
обращается в нуль лишь для вырожденного распределения:
если 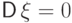 , то
, то  п.н. и наоборот.
п.н. и наоборот.
Доказательство.
Дисперсия есть математическое ожидание
почти наверное неотрицательной случайной величины 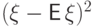 ,
и неотрицательность дисперсии следует из свойства (E5).
Далее, по свойству (E6) из равенства дисперсии нулю вытекает
,
и неотрицательность дисперсии следует из свойства (E5).
Далее, по свойству (E6) из равенства дисперсии нулю вытекает  п.н., т.е.
п.н., т.е. 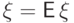 п.н.
И наоборот,
если
п.н.
И наоборот,
если  п.н., то
п.н., то  .
.
(D4)
Дисперсия не зависит от сдвига случайной величины на
постоянную: 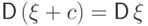 .
.
(D5)
Если  и
и  независимы, то
независимы, то  .
.
Доказательство. Действительно,

Замечание См. замечание 2.
Следствие 14.
Если  и
и  независимы, то
независимы, то
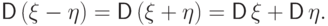
Доказательство. Из свойств (D5) и (D2) получим
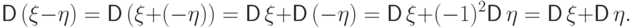
Следствие 15.
Для произвольных случайных величин  и
и  с конечными
вторыми моментами имеет место равенство
с конечными
вторыми моментами имеет место равенство
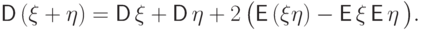
(D6)
Минимум среднеквадратического отклонения
случайной величины  от точек числовой прямой
есть среднеквадратическое отклонение
от точек числовой прямой
есть среднеквадратическое отклонение  от ее математического
ожидания:
от ее математического
ожидания:  .
.
Доказательство. Сравним величину 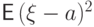 с
дисперсией:
с
дисперсией:
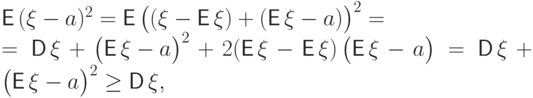
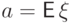 .
.Математические ожидания и дисперсии стандартных распределений
Пример 54. (вырожденное распределение 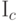 )
Математическое ожидание и дисперсию этого распределения мы знаем из свойств
(E2) и (D3):
)
Математическое ожидание и дисперсию этого распределения мы знаем из свойств
(E2) и (D3):  ,
, 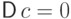 .
.
Пример 55 (распределение Бернулли 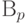 ).
Вычислим два момента и дисперсию:
).
Вычислим два момента и дисперсию: 
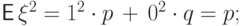
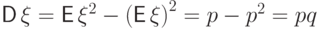 .
.
Пример 56 (биномиальное распределение 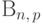 ).
Используем свойство устойчивости биномиального распределения
относительно суммирования - лемму 2.
Возьмем на каком-нибудь вероятностном пространстве
).
Используем свойство устойчивости биномиального распределения
относительно суммирования - лемму 2.
Возьмем на каком-нибудь вероятностном пространстве  независимых
случайных величин
независимых
случайных величин  с
распределением Бернулли
с
распределением Бернулли 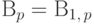 .
Тогда их сумма
.
Тогда их сумма  имеет распределение
имеет распределение 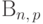 и по свойству (E4) получаем
и по свойству (E4) получаем
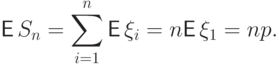
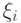 независимы, и дисперсия каждой равна
независимы, и дисперсия каждой равна  , то
, то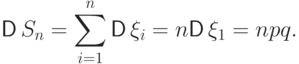
 ,
, 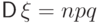 для
для 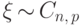 .
.Пример 57 (геометрическое распределение 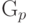 ).
Вычислим математическое ожидание
).
Вычислим математическое ожидание  :
:
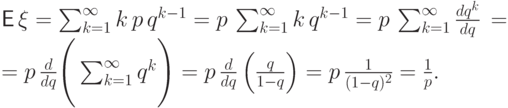
 :
: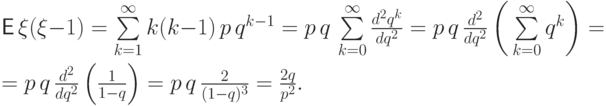
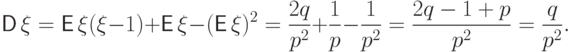
Пример 58 (распределение Пуассона 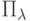 ).
Вычислим математическое ожидание
).
Вычислим математическое ожидание  :
:

![{\mathsf E\,}\xi^{[m]}={\mathsf E\,}\xi(\xi-1)\ldots(\xi-m+1)](/sites/default/files/tex_cache/81ae451188e1d6227539e54269fc449a.png) порядка
порядка  .
Так, второй факториальный момент
.
Так, второй факториальный момент  равен
равен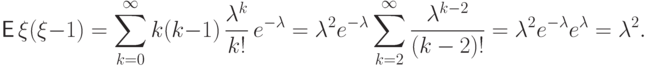
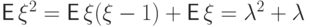 и
и  .
.Пример 59 (равномерное распределение 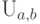 ).
Математическое ожидание
).
Математическое ожидание 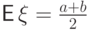 найдено в
примере 49.
Вычислим второй момент:
найдено в
примере 49.
Вычислим второй момент:
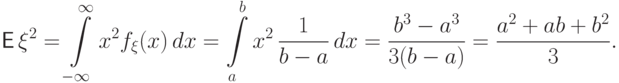
 .
.Пример 60 (стандартное нормальное распределение 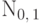 ).
Математическое ожидание этого распределения существует, поскольку
).
Математическое ожидание этого распределения существует, поскольку
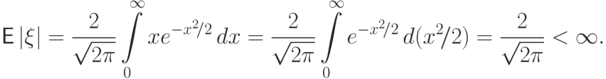
 равно нулю:
равно нулю:
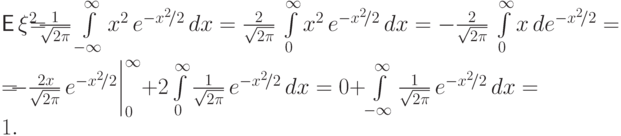
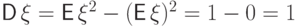 .
.Пример 61. (нормальное распределение 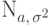 )
Мы знаем, что если
)
Мы знаем, что если  , то
, то 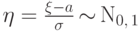 . Математическое
ожидание
. Математическое
ожидание 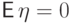 и дисперсия
и дисперсия 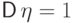 стандартного
нормального
распределения вычислены выше.
Тогда
стандартного
нормального
распределения вычислены выше.
Тогда
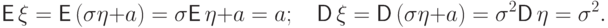
Итак, параметры  и
и  нормального
распределения суть его математическое
ожидание и дисперсия.
нормального
распределения суть его математическое
ожидание и дисперсия.
Пример 62 (показательное распределение 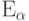 ).
).
Найдем для произвольного  момент порядка
момент порядка 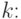
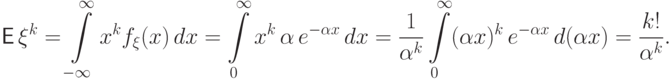
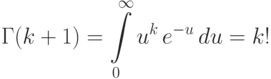
 находим
находим
Пример 63 (стандартное распределение Коши  ).
Математическое ожидание распределения Коши не существует,
так как расходится интеграл
).
Математическое ожидание распределения Коши не существует,
так как расходится интеграл
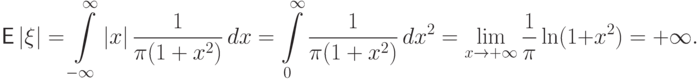
 .
Поэтому не существуют ни дисперсия, ни моменты более высоких порядков этого
распределения.
То же самое можно сказать про распределение Коши
.
Поэтому не существуют ни дисперсия, ни моменты более высоких порядков этого
распределения.
То же самое можно сказать про распределение Коши  .
.Пример 64 (распределение Парето).
У распределения Парето существуют только моменты порядка  ,
поскольку
,
поскольку
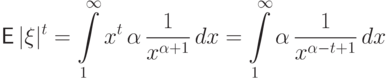
 , когда подынтегральная функция на
бесконечности
ведет себя как
, когда подынтегральная функция на
бесконечности
ведет себя как 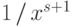 , где
, где  .
.