|
Символы кириллицы выводит некорректно. Как сделать чтобы выводился читабельный текст на русском языке? Тип приложения - не Qt, Qt Creator 4.5.0 основан на Qt 5.10.0. Win7.
|
Опубликован: 07.03.2015 | Уровень: для всех | Доступ: свободно | ВУЗ: Компания ALT Linux
Лекция 9:
Структуры в языке C++
9.2 Библиотеки для работы с комплексными числами
Работа с комплексными числами в C++ реализована с помощью библиотеки complex. Подключение этой библиотеки даёт возможность применять операции +, _, *, / для работы не только с вещественными, но и с комплексными числами.
Перед подключением библиотеки complex обязательно необходимо подключить библиотеку math.h.
Для определения переменной типа комплексное число используется оператор.
complex <тип_переменной> имя_переменной;
Здесь тип_переменной — это любой допустимый в C++ числовой тип данных (int, long int, double, float и т. д.), описывающий действительную и мнимую части комплексного числа. Например,
complex <float > x, y, z [ 5 ], * r; complex <double> a; complex <int> a, b, c;
Для организации ввода-вывода комплексных чисел можно использовать библиотеку iostream и стандартные конструкции cin, cout. Например,
#include <iostream>
#include <math.h>
#include <complex>
using namespace std;
int main ( int arg c, char ** argv )
{
complex <double> b, c; //Описание комплексных чисел.
cout<<" b = "; cin>>b; //Ввод комплексного числа b.
cout<<" c = "; cin>>c; //Ввод комплексного числа c.
cout<<" b / c = "<<b/ c; //Вывод частного комплексных чисел
return 0;
}В результате получим:
b=(1.24,-6.12) c=(9.01,-11.22) b/c=(0.385567,-0.199105)
Обратите внимание, что при вводе комплексных чисел с клавиатуры действительная и мнимая части вводятся в скобках через запятую:
(действительная_часть, мнимая_часть)
Далее приведён пример присваивания комплексным переменным реальных значений при их описании:
complex <double> z ( 4.0, 1.0 ); complex <int> r ( 4, -7);
Следующий пример демонстрирует, как из двух числовых значений можно составить комплексное число:
#include <iostream>
#include <math.h>
#include <complex>
using namespace std;
int main ( int arg c, char ** argv )
{
double x1, y1;
x1=-2.3;
y1 = 8.1;
complex <double> b ( x1, y1 ); //Формирование комплексного числа b
//с действительной частью x1 и мнимой y1.
cout<<" b ^ 2 = "<<b*b; //Вывод квадрата комплексного числа.
return 0;
}В табл. 9.1 представлены основные математические функции для работы с комплексными числами.
| Прототип функции | Описание функции |
|---|---|
| double abs(complex z) | Возвращает модуль комплексного числа  . |
| double arg(complex z) | Возвращает значение аргумента комплексного числа
|
| complex conj(complex z) | Возвращает число комплексно сопряжённое числу
|
| complex cos(complex z) | Возвращает косинус комплексного числа
|
| complex cosh(complex z) | Возвращает гиперболический косинус комплексного числа . |
| complex exp(complex z) | Возвращает экспоненту комплексного числа . |
| double imag(complex z) | Возвращает мнимую часть комплексного числа . |
| complex log(complex z) | Возвращает натуральный логарифм комплексного числа
|
| complex log10(complex z) | Возвращает десятичный логарифм комплексного числа . |
| double norm(complex z) | Возвращает квадрат модуля комплексного числа . |
| complex pow(complex x, complex y) | Возвращает степень комплексного числа . |
| complex polar(double mag, double angle) | Формирует комплексное число с модулем  и аргументом 
|
| double real(complex z) | Возвращает действительную часть комплексного числа
|
| complex sin(complex z) | Возвращает синус комплексного числа
|
| complex sinh(complex z) | Возвращает гиперболический синус комплексного числа . |
| complex sqrt(complex z) | Возвращает квадратный корень комплексного числа
|
| complex tan(complex z) | Возвращает тангенс комплексного числа
|
| complex tanh(complex z) | Возвращает гиперболический тангенс комплексного числа . |
Далее приведён текст программы, демонстрирующий работу с некоторыми функциями из табл. 9.1.
#include <iostream>
#include <math.h>
#include <complex>
using namespace std;
int main ( )
{
complex <double> x ( 4, -6);
complex <double> y (-7, 2 );
cout<<" x * y = "<<x*y<<endl;
cout<<" sin ( x ) * cos ( y ) = "<<sin ( x ) * cos ( y )<<endl;
cout<<" conj ( x ) * ln ( y ) = "<<conj ( x ) * log ( y )<<endl;
cout<<" sh ( y ) = "<<sinh ( y )<<endl;
return 0;
}Результаты работы программы с некоторыми функциями комплексного аргумента:
x*y=(-16,50) sin(x)*cos(y)=(-747.159,10.2102) conj(x)*ln(y)=(-9.23917,23.364) sh(y)=(228.18,498.583)
Задача 9.3. Вычислить 
.
Если провести аналитические преобразования, то получим следующее:
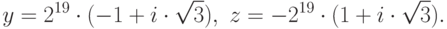
Проверим эти вычисления с помощью программы на C++. Результаты работы программы подтверждают аналитические вычисления.
#include <iostream>
#include <math.h>
#include <complex>
using namespace std;
int main ( )
{
complex <double> b ( sqrt ( 3 ),-1), y;
y=pow ( b, 20 );
cout<<" y = "<<y<<endl;
cout<<real ( y ) /pow ( 2, 1 9 )<<" \t ";
cout<<imag ( y ) /pow ( 2, 1 9 )<<" \n ";
complex <double> a ( 1, sqrt ( 3 ) ), c (1, -1), z;
z=pow ( a / c, 40 );
cout<<" z = "<<z<<endl;
cout<<real ( z ) /pow ( 2, 19 )<<" \t ";
cout<<imag ( z ) /pow ( 2, 19 )<<" \n ";
return 0;
}Результаты работы программы к задаче 9.3:
b=(1.73205,-1)y=(-524288,908093) -1 1.73205 z=(-524288,-908093) -1 -1.73205
Операции с массивами, элементами которых являются комплексные числа, осуществляются так же, как и с обычными переменными. В качестве примера рассмотрим следующие задачи.
Сергей Радыгин
Юрий Герко
|
Кому удалось собрать пример из раздела 13.2 Компоновка (Layouts)? Если создавать проект по изложенному алгоритму, автоматически не создается файл mainwindow.cpp. Если создавать этот файл вручную и добавлять в проект, сборка не получается - компилятор сообщает об отсутствии класса MainWindow. Как правильно выполнить пример? |