Использование функций при программировании на C++

4.5 Рекурсивные функции

Под рекурсией в программировании понимают функцию, которая вызывает сама себя. Рекурсивные функции чаще всего используют для компактной реализации рекурсивных алгоритмов. Классическими рекурсивными алгоритмами могут быть возведение числа в целую положительную степень, вычисление факториала. С другой стороны, любой рекурсивный алгоритм можно реализовать без применения рекурсий. Достоинством рекурсии является компактная запись, а недостатком — расход памяти на повторные вызовы функций и передачу параметров, существует опасность переполнения памяти.

Рассмотрим применение рекурсии на примерах [7, 8].

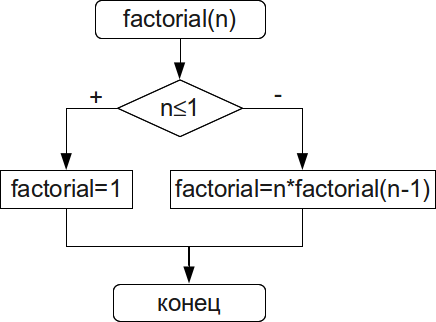
Задача 4.8. Вычислить факториал числа .

Вычисление факториала подробно рассмотрено в задаче 3.12 (рис. 3.25). Для решения этой задачи с применением рекурсии создадим функцию factoial, алгоритм которой представлен на рис. 4.10.

Рис. 4.10. Рекурсивный алгоритм вычисления факториала

Текст программы с применением рекурсии:

#include <iostream>
using namespace std;
long int factorial ( int n )
{
	if ( n<=1)
	return n;
	else
	return n*factorial ( n-1);
}
int main ( )
{
	int i; long int f;
	cout<<"i="; cin >>i;
	f=factorial ( i );
	cout<<i <<" !="<<f<<"\n";
	return 0;
}
				

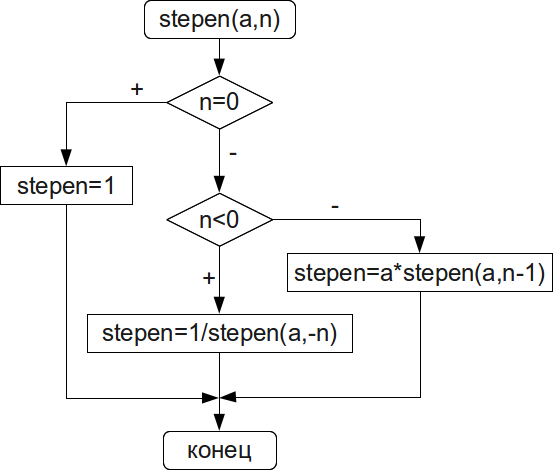
Задача 4.9. Вычислить -ю степень числа ( — целое число).

Результатом возведения числа в целую степень является умножение этого числа на себя раз. Но это утверждение верно только для положительных значений . Если принимает отрицательные значения, то .В случае .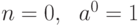

Для решения задачи создадим рекурсивную функцию stepen, алгоритм которой представлен на рис. 4.11.

Рис. 4.11. Рекурсивный алгоритм вычисления степени числа

Текст программы с применением рекурсии:

#include <iostream>
using namespace std;
float stepen ( float a, int n )
{
	if ( n==0)
		return 1;
	else if ( n<0)
		return 1/ stepen ( a,-n );
	else
	return a * stepen ( a, n-1);
}
int main ( )
{
	int i; float s, b;
	cout<<"b="; cin >>b;
	cout<<"i="; cin >>i;
	s=stepen ( b, i );
	cout<<"s="<<s<<"\n";
	return 0;
}
				

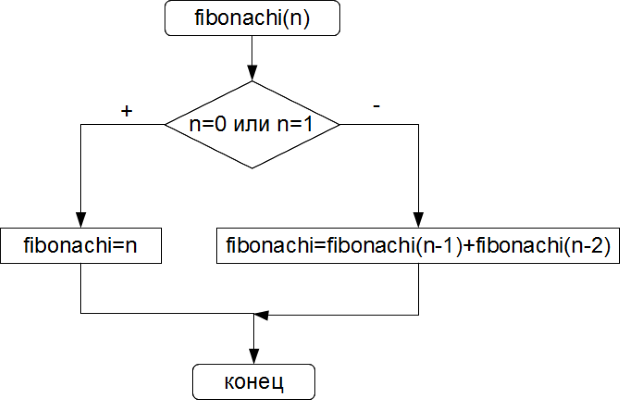
Задача 4.10. Вычислить -е число Фибоначчи.

Если нулевой элемент последовательности равен нулю, первый — единице, а каждый последующий представляет собой сумму двух предыдущих, то это последовательность чисел Фибоначчи (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ... ).

Алгоритм рекурсивной функции fibonachi изображён на рис. 4.12.

Рис. 4.12. Рекурсивный алгоритм вычисления числа Фибоначчи

Текст программы:

#include <iostream>
using namespace std;
long int fibonachi ( unsigned int n )
{
	if ( ( n==0) | | ( n==1))
	return n;
	else
	return fibonachi ( n -1)+fibonachi ( n-2);
}
int main ( )
{
	int i; long int f;
	cout<<"i="; cin >>i;
	f=fibonachi ( i );
	cout<<"f="<<f<<"\n";
	return 0;
}