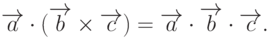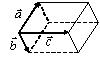|
Добрый день. Подскажите пожалуйста, я прошел ваш курс Введение в линейную алгебру: Информация, - сдал экзамен и у меня высветилось окно, где необходимо оформить доставку сертификата. Однако, я случайно закрыл это окно и теперь не могу найти этот подраздел, чтобы оформить доставку. Где можно это найти? |
Скалярное произведение векторов. Свойства. Векторное произведение векторов. Свойства. Смешанное произведение векторов. Свойства
3. Векторное произведение двух векторов.
Определение 15. Под векторным произведением векторов  и
и  понимают вектор
понимают вектор  , имеющий длину и направленный перпендикулярно к плоскости
, имеющий длину и направленный перпендикулярно к плоскости  , определяемой векторами
, определяемой векторами  и
и  , причем так, что векторы
, причем так, что векторы  ,
,  и
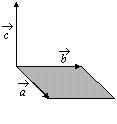
и  образуют правую тройку векторов (рис. 6.2).
образуют правую тройку векторов (рис. 6.2).
Можно заметить, что длина вектора  численно равна площади параллелограмма, построенного на векторах
численно равна площади параллелограмма, построенного на векторах  и
и  как на сторонах ( это геометрический смысл векторного произведения ).
как на сторонах ( это геометрический смысл векторного произведения ).
Векторное произведение обозначают:  или
или ![[\overrightarrow{a},\overrightarrow{b}]](/sites/default/files/tex_cache/b7ef688dc6d7e64ff34e8ef303a426ee.png) . Очевидно, что
. Очевидно, что  (из определения векторного произведения), т.е. векторное произведение не коммутативно. Векторное произведение также не ассоциативно,
(из определения векторного произведения), т.е. векторное произведение не коммутативно. Векторное произведение также не ассоциативно,  , в чем можно легко убедиться самостоятельно. Векторное произведение подчиняется только распределительному закону:
, в чем можно легко убедиться самостоятельно. Векторное произведение подчиняется только распределительному закону:
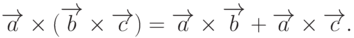
Так как 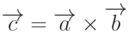 перпендикулярен плоскости, определяемой векторами
перпендикулярен плоскости, определяемой векторами  и
и  , и численно равен площади параллелограмма, сторонами которого являются векторы
, и численно равен площади параллелограмма, сторонами которого являются векторы  и
и  , то, очевидно, что проекции вектора на оси ординат 0х, 0у и 0z будут численно равны площадям проекций указанного параллелограмма на соответствующие координатные плоскости:
, то, очевидно, что проекции вектора на оси ординат 0х, 0у и 0z будут численно равны площадям проекций указанного параллелограмма на соответствующие координатные плоскости:
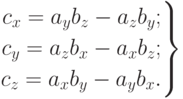
Тогда векторное произведение 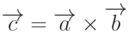 расписывается по базису
расписывается по базису 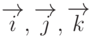 следующим образом3Из этого равенства видно, что вектор
следующим образом3Из этого равенства видно, что вектор 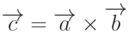 является антисимметричным тензором третьего ранга.:
является антисимметричным тензором третьего ранга.:

Замечание 1. 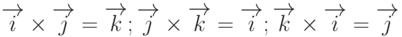 . Используя это свойство векторного произведения проверяют ортогональность трех векторов. Если векторное произведение двух любых из трех векторов равно третьему вектору, то тогда говорят , что векторы ортогональны (или линейно независимы) между собой.
. Используя это свойство векторного произведения проверяют ортогональность трех векторов. Если векторное произведение двух любых из трех векторов равно третьему вектору, то тогда говорят , что векторы ортогональны (или линейно независимы) между собой.
Замечание 2. Двойное векторное произведение 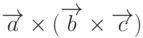 есть вектор
есть вектор 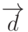 , компланарный векторам
, компланарный векторам  и
и  , вычисляемый по формуле
, вычисляемый по формуле
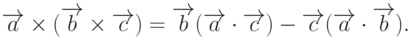
Замечание 3.  .
.
4. Смешанное произведение векторов.
Определение 16. Смешанным произведением векторов  ,
,  и
и  назовем число К, равное объему параллелепипеда, построенного на этих векторах (рис. 6.3) и вычисляемое как:
назовем число К, равное объему параллелепипеда, построенного на этих векторах (рис. 6.3) и вычисляемое как:
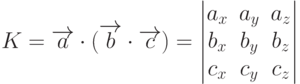
 ,
,  и
и  компланарны, то
компланарны, то  .
.Определение 17. Скалярным произведением двух векторных произведений назовем число, равное выражению
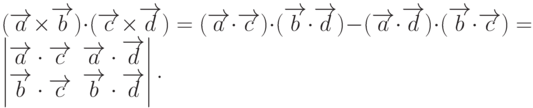
Заметим, что 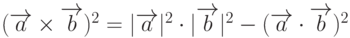 .
.
Из определения смешанного произведения следует интересный факт, что произведение не зависит от порядка следования векторов в смешанном произведении, так как объем параллелепипеда (положительный или отрицательный) зависит только от расположения этих векторов в пространстве (левая или правая тройка) потому, что является псевдоскаляром. Следовательно, можно записать
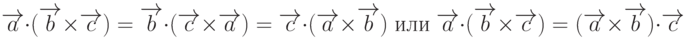
Это замечательное свойство смешанного произведения служит обоснованием упрощения записи смешанного произведения: