|
Здравствуйте, прошел курс "Концептуальное проектирование систем в AnyLogic и GPSS World". Можно ли получить по нему сертификат? У нас в институте требуют сертификаты для создания портфолио. |
Решение обратных задач в AnyLogic
Решение обратных задач средствами GPSS World было рассмотрено в главах "Модель обработки запросов сервером" и "Модель процесса изготовления в цехе деталей" . Теперь приступим к решению этих же задач в AnyLogic.
Определение среднего времени обработки группы запросов сервером
- В п. 1.2.6 была сохранена модель простой эксперимент с именем Сервер Обратная задача. Откройте её.
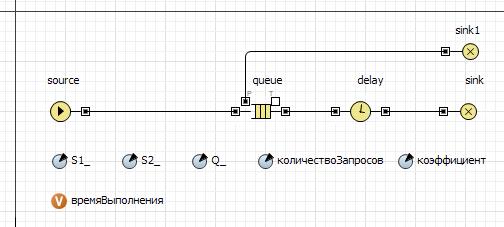
- Удалите из модели объекты презентации и вывода статистики. Она должна иметь объекты, показанные на рис. 11.1.
- Добавьте два элемента Параметр и один элемент Простая переменная. Дайте имена, как на рис. 11.1.
- Тип элемента количествоЗапросов int. В поле Значение по умолчанию: введите 29. Это целая часть количества обработанных запросов при решении прямой задачи.
- Элемент коэффициент как и в GPSS-модели предназначен для учёта дробной части количества обработанных запросов (см. п. 1.3). Его тип double. Введите в поле Значение по умолчанию: 1.
- Тип элемента времяВыполнения double.
- Выделите блок sink и в поле Действие при входе: введите Java код:
if( sink.in.count() == количествоЗапросов ){ времяВыполнения = time(); stopSimulation(); }
Этот код сравнивает заданное количество запросов в группе (в данном случае 29) с обработанным количеством запросов. При равенстве заданных и обработанных запросов переменной времяВыполнения присваивается величина текущего модельного времени, то есть время обработки заданной группы запросов в одном прогоне модели, и простой эксперимент останавливается.
Для выполнения заданного количества прогонов создайте эксперимент варьирования параметров.
- В панели Проект щелкните правой кнопкой мыши элемент модели и из контекстного меню выберите Создать эксперимент.
- В появившемся диалоговом окне из списка Тип эксперимента: выберите Варьирование параметров.
- В поле Имя оставьте имя эксперимента, рекомендованное системой.
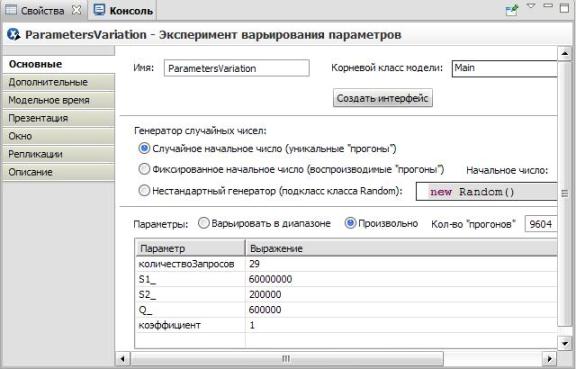
- Щелкните кнопку Готово. Появится страница Основные панели Свойства (рис. 11.2). Установите свойства согласно рис. 11.2.
- Перейдите на страницу Дополнительные. В поле Код инициализации эксперимента: введите data.reset();. А в поле Действие после прогона модели:
data.add( time()/коэффициент );
- В эксперименте Варьирование параметров, как вы помните, в отличие от эксперимента Оптимизация интерфейс создает пользователь.
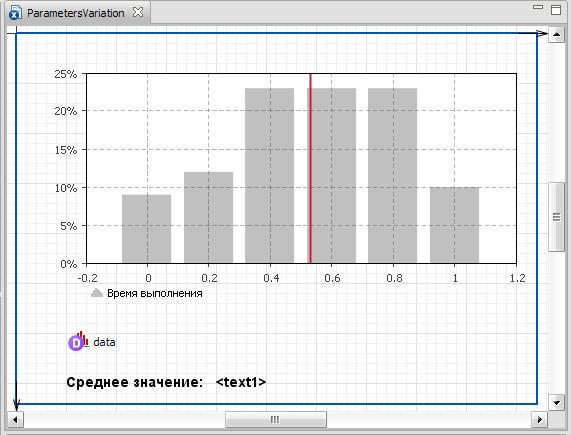
- Создайте интерфейс, показанный на рис. 11.3. Здесь вы видите гистограмму, которая будет отображать время выполнения группы запросов. Начните с нажатия Создать интерфейс.
- Перетащите элемент Гистограмма из палитры Статистика на диаграмму активного класса. На странице Основные установите флажок Отображать среднее. Оставьте флажок Отображать плотность вероятности.
- Щёлкните Добавить данные.
- Установите Заголовок: Время выполнения. Набор данных: data. Цвет плотности вер-ти: silver. Цвет линии среднего: crimson. Установите Не обновлять автоматически.
- Перетащите элемент Данные гистограммы. В поле Имя: введите data. Остальные свойства оставьте установленными по умолчанию.
- Добавьте элемент text и введите Среднее значение:.
- Добавьте второй элемент text. Оставьте имя, предложенное системой. Перейдите на страницу Динамические и в поле Текст: введите data.mean().
- Построение Эксперимента варьирование параметров завершено. Запустите его. При наличии ошибок, устраните их.
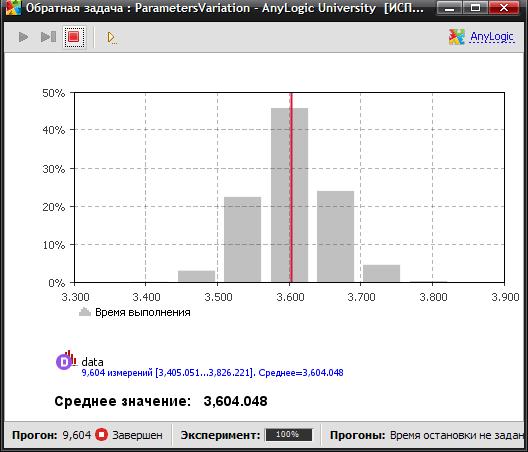
Далее проведём по четыре эксперимента в AnyLogic и GPSS World. Результаты одного из экспериментов при количестве прогонов 29,16 показаны на рис. 11.4. Результаты всех экспериментов сведены в табл. 11.1.
Для первого эксперимента исходные данные были введены в ходе предыдущих построений. Для экспериментов 2…4 данные вводятся из табл. 11.1. Например, для второго эксперимента значение по умолчанию параметра количествоЗапросов заменяется на 291, а значение по умолчанию параметра коэффициент учёта дробной части - на 10 на диаграмме простого эксперимента.
| Параметры и показатели | Системы моделирования | |
|---|---|---|
| GPSS World | AnyLogic | |
| Эксперимент 1 | ||
| Количество запросов | 29 | 29 |
| Коэффициент учёта дробной части | 1 | 1 |
| Машинное время выполнения модели | 2 cек | 1,3 cек |
| Время выполнения группы запросов | 3589,688 | 3781,755 |
 | ||
| Эксперимент 2 | ||
| Количество запросов | 291 | 291 |
| Коэффициент учёта дробной части | 10 | 10 |
| Машинное время выполнения модели | 24 cек | 7 cек |
| Время выполнения группы запросов | 3596,113 | 3614,877 |
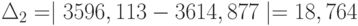 | ||
| Эксперимент 3 | ||
| Количество запросов | 2916 | 2916 |
| Коэффициент учёта дробной части | 100 | 100 |
| Машинное время выполнения модели | 4 мин 48 cек | 44 cек |
| Время выполнения группы запросов | 3603,039 | 3604,676 |
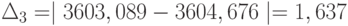 | ||
| Эксперимент 4 | ||
| Количество запросов | 29161 | 29161 |
| Коэффициент учёта дробной части | 1000 | 1000 |
| Машинное время выполнения модели | 40 мин 48 cек | 11 мин 17 сек |
| Время выполнения группы запросов | 3604,526 | 3603,182 |
 | ||
По результатам экспериментов видно, что по мере учёта дробной части разница между средними временами обработки группы запросов сервером, полученными в GPSS-модели и AnyLogic-модели уменьшается: 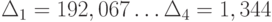 . При этом среднее время в обеих моделях приближается к времени моделирования (3600) в прямой задаче. То что оно приближается "справа", объясняется определением одного прогона модели обработкой заданного количества запросов, а не временем моделирования.
. При этом среднее время в обеих моделях приближается к времени моделирования (3600) в прямой задаче. То что оно приближается "справа", объясняется определением одного прогона модели обработкой заданного количества запросов, а не временем моделирования.
Определение среднего времени изготовления деталей
В "Модель процесса изготовления в цехе деталей" мы рассмотрели методику решения обратной задачи в GPSS World и прямой задачи в AnyLogic. Теперь решим обратную задачу и в AnyLogic.
- Откройте модель Изготовление_в_цехе_деталей. Сохраните с именем Изготовление_в_цехе_деталей Обратная задача.
- Добавьте на диаграмму класса Main два элемента Параметр и один элемент Простая переменная.
- Тип параметра КоличествоДеталей int. В поле Значение по умолчанию: введите 9017. Это целая и дробная части количества изготовленных деталей при решении прямой задачи, записанные как целое число.
- Параметр коэффициент как и в GPSS-модели предназначен для учёта дробной части количества обработанных запросов. Его тип double. Введите в поле Значение по умолчанию: 1000.
- Тип элемента времяИзготовления double.
- Перейдите на диаграмму Kontrol. Выделите блок sink сегмента Склад готовых изделий и в поле Действие при входе: введите вместо имеющегося там Java код:
if( склГотДет.in.count() == get_Main().количествоДеталей ){ get_Main().времяИзготовления=time(); stopSimulation(); }
Для выполнения заданного количества прогонов также как и в предыдущем случае создайте эксперимент варьирования параметров.
- В панели Проект щелкните правой кнопкой мыши элемент модели и из контекстного меню выберите Создать эксперимент.
- В появившемся диалоговом окне из списка Тип эксперимента: выберите Варьирование параметров.
- В поле Имя оставьте имя эксперимента, рекомендованное системой.
- Щелкните кнопку Готово. Появится страница Основные панели Свойства (см. рис. 11.2). Установите свойства согласно рис. 11.2, кроме количества прогонов. В соответствующее поле введите 16641.
- Перейдите на страницу Дополнительные.
- В поле Код инициализации эксперимента: введите А в поле Действие после прогона модели:
data.reset();
data.add( time()/коэффициент );
- Перейдите на страницу Модельное время. В поле Остановить выберите из списка Нет.
- Постройте интерфейс эксперимента также как и предыдущей модели (п. 11.1), выполнив пп. 7…13.
- Построение Эксперимента варьирование параметров завершено. Запустите его. При наличии ошибок, устраните их.
При построении мы ввели данные для проведения эксперимента с учётом всех трёх знаков после запятой.
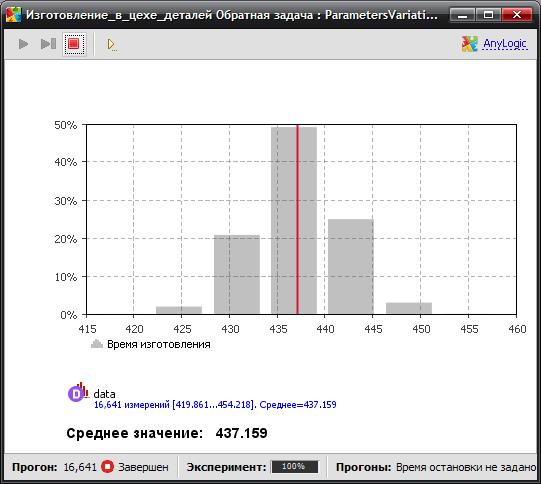
Проведём эксперимент в AnyLogic. Результат решения обратной задачи показан на рис. 11.5.
| Параметры и показатели | Системы моделирования | |
|---|---|---|
| GPSS World | AnyLogic | |
| Количество деталей | 9017 | 9017 |
| Коэффициент учёта дробной части | 1000 | 1000 |
| Машинное время выполнения модели | 2 час 23 мин 48 сек | 30 мин 54 cек |
| Время изготовления деталей | 7,275 час | 7,286 час |
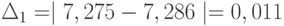 | ||
В табл. 11.2 сведены результаты экспериментов решения обратной задачи в GPSS World и AnyLogic. Они свидетельствуют об их адекватности, так как 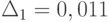 . Если, конечно, исследователя устраивает такое
. Если, конечно, исследователя устраивает такое 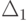 .
.
Но машинное время выполнения модели в GPSS World примерно в пять раз больше, чем в AnyLogic, и равно 2 час 23 мин 43 сек.
Обратим внимание ещё раз на то, что время изготовления при повторных запусках эксперимента может отличаться, так как выбраны были уникальные прогоны модели.
Заключение
Целью настоящего учебного пособия являлось приобретение навыков разработки постановок задач на концептуальное проектирование, освоение техники ИМ, планирования, проведения и обработки данных компьютерных экспериментов для принятия проектных решений. ИМ выбрано потому как мировая практика научных исследований свидетельствует о том, что методы ИМ занимают около 70 % в общем объеме исследовательского инструментария. В настоящее время в ИМ выделяют три подхода: системной динамики, дискретно-событийный и агентный. Из этих подходов в рамках указанных дисциплин изучается дискретно-событийный подход, обеспечивающий универсальность и эффективность ИМ. Он ориентирован на исследование широкого класса сложных систем, представимых в виде систем массового обслуживания, в том числе и систем военного назначения.
При изучении в рамках различных дисциплин ИМ, а также в практике создания моделей неизбежно возникает вопрос о выборе среды разработки, адекватности систем моделирования: будут ли реализованы так же все функции моделируемой системы? Будут ли получены одинаковые результаты моделирования?
Вспомним Р. Шеннона [24]: "Подобно всем мощным средствам, существенно зависящим от искусства их применения, имитационное моделирование способно дать либо очень хорошие, либо очень плохие результаты".
В пособии на детально разработанных и реализованных средствами GPSS World и AnyLogic моделях объектов с разнородными протекающими в них процессами помимо основной цели также демонстрируется достаточная адекватность GPSS World и AnyLogic относительно результатов моделирования.
В задачу автора не входило дать кардинальную оценку, какая система ИМ и в каких случаях предпочтительна. Читатель вправе сделать это самостоятельно, исходя из целей создания своей имитационной модели проектируемой системы и опираясь на приведенные в пособии результаты.