| Украина |
Задачи высшей математики с Maxima
3.4 Экстремумы функций
3.4.1 Отыскание максимумов и минимумов
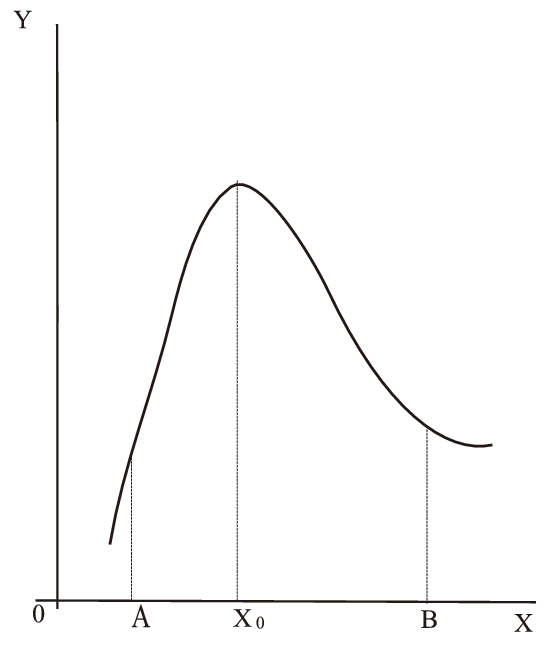
Точки, где достигается наибольшее или наименьшее значение функции называются соответственно точками максимума или минимума функции.
Определение 1. Точка  называется точкой максимума функции
называется точкой максимума функции  , если в некоторой окрестности точки
, если в некоторой окрестности точки  выполняется неравенство
выполняется неравенство  (см. рис. 3.3).
(см. рис. 3.3).
Определение 2. Точка  называется точкой минимума функции
называется точкой минимума функции  , если в некоторой окрестности точки
, если в некоторой окрестности точки  выполняется неравенство
выполняется неравенство  (см. рис. 3.3).
(см. рис. 3.3).
Значения функции в точках  и
и  называются соответственно максимумом и минимумом функции. Максимум и минимум функции объединяются общим названием экстремума функции.
называются соответственно максимумом и минимумом функции. Максимум и минимум функции объединяются общим названием экстремума функции.
Экстремум функции часто называют локальным экстремумом, подчеркивая тем самым, что понятие экстремума связано лишь с достаточно малой окрестностью точки  . Так что на одном промежутке функция может иметь несколько экстремумов, причем может случиться так, что минимум в одной точке больше максимума в другой.
. Так что на одном промежутке функция может иметь несколько экстремумов, причем может случиться так, что минимум в одной точке больше максимума в другой.
Наличие максимума (или минимума) в отдельной точке промежутка  вовсе не означает, что в этой точке функция
вовсе не означает, что в этой точке функция  принимает наибольшее (наименьшее) значение на этом промежутке (или, как говорят имеет глобальный максимум (минимум)).
принимает наибольшее (наименьшее) значение на этом промежутке (или, как говорят имеет глобальный максимум (минимум)).
3.4.1.1 Теорема Ферма
Теорема Ферма. Если дифференцируемая на промежутке  функция
функция 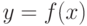 достигает наибольшего или наименьшего значения в внутренней точке
достигает наибольшего или наименьшего значения в внутренней точке  , то тогда производная функции в этой точке равна нулю, т.е.
, то тогда производная функции в этой точке равна нулю, т.е.  .
.
Пусть функция 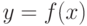 дифференцируема на промежутке
дифференцируема на промежутке  и в точке
и в точке 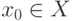 принимает наименьшее значение (см. рис. 3.4).
принимает наименьшее значение (см. рис. 3.4).
Тогда

 и, следовательно
и, следовательно

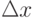 и независимо от знака
и независимо от знака 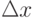 .
.Поэтому
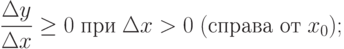
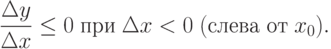
Переходя к пределу справа и слева получим

 , то пределы
справа и слева равны
, то пределы
справа и слева равны

 .
.Аналогичную последовательность рассуждений можно построить и для максимума.
Теорему Ферма часто называют необходимым условием экстремума дифференцируемой функции.
Геометрический смысл теоремы Ферма: в точке экстремума, достигаемого внутри промежутка  , касательная к графику функции параллельна оси абсцисс.
, касательная к графику функции параллельна оси абсцисс.
3.4.1.2 Необходимое условие экстремума
Если в точке  дифференцируемая функция
дифференцируемая функция  имеет экстремум, то в некоторой окрестности этой точки выполняются условия теоремы Ферма, и следовательно, производная функции в этой точке равна нулю, т.е.
имеет экстремум, то в некоторой окрестности этой точки выполняются условия теоремы Ферма, и следовательно, производная функции в этой точке равна нулю, т.е.  . Но функция может иметь экстремум и в точках, в которых она не дифференцируема. Так, например, функция
. Но функция может иметь экстремум и в точках, в которых она не дифференцируема. Так, например, функция  имеет экстремум (минимум) в точке
имеет экстремум (минимум) в точке 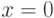 , но не дифференцируема в ней. Функция
, но не дифференцируема в ней. Функция
![y=\sqrt[3]{x^2}](/sites/default/files/tex_cache/4b63d449fe81825456b97639e662b5bb.png)
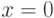 минимум, а ее производная в этой точке бесконечна:
минимум, а ее производная в этой точке бесконечна: ![y'=\displaystyle{\frac{2}{3\sqrt[3]{x}}},\ y'(0)=\infty](/sites/default/files/tex_cache/5c75875be6a4bb906777da4ae15586e9.png) .
.Поэтому необходимое условие экстремума может быть сформулировано следующим образом.
Для того чтобы функция 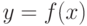 имела экстремум в точке
имела экстремум в точке  , необходимо, чтобы ее производная в этой точке равнялась нулю (
, необходимо, чтобы ее производная в этой точке равнялась нулю ( ) или не существовала.
) или не существовала.
Точки, в которых выполнено необходимое условие экстремума, называются критическими (или стационарными). Но критическая точка не обязательно является точкой экстремума.
Пример. Найти критические точки функции и убедиться в наличии или отсутствии экстремума в этих точках: 1.  2.
2.  .
.
-
 при
при 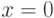 . В точке
. В точке 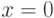 функция
функция  имеет минимум.
имеет минимум. -
 при
при 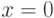 . В точке
. В точке 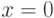 функция
функция  не имеет экстремума. Функция
не имеет экстремума. Функция  возрастает на всей числовой оси.
возрастает на всей числовой оси.
Итак, для нахождения экстремумов функции требуется дополнительное исследование критических точек.
Пример: Исследовать на наличие экстремума следующую функцию
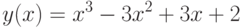
Задаём исследуемую функцию
(%i1) f(x):=x^3-3*x^2+3*x+2;
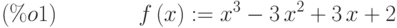
Производную в форме функции определяем явно, используя функцию 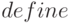
(%i2) define(df(x),diff(f(x),x));

Решая уравнение 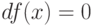 (т.е.
(т.е.  , находим критические точки
, находим критические точки
(%i3) solve(df(x)=0,x);
![[x=1]\leqno{(\%o3) }](/sites/default/files/tex_cache/ab475b21fa21cbb80cac415432b61582.png)
В данном случае критическая точка одна —  .
.
3.4.1.3 Первое достаточное условие экстремума
Теорема. Если при переходе через точку  производная дифференцируемой функции
производная дифференцируемой функции 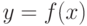 меняет свой знак с плюса на минус, то точка
меняет свой знак с плюса на минус, то точка  есть точка максимума функции
есть точка максимума функции 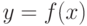 , а если с минуса на плюс, то — точка минимума.
, а если с минуса на плюс, то — точка минимума.
Пусть производная меняет знак с плюса на минус, т.е. в некотором интервале ( ) производная положительна (
) производная положительна ( ), а в некотором интервале (
), а в некотором интервале (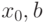 ) — отрицательна (
) — отрицательна ( ) (см. рис. 3.5). Тогда в соответствии с достаточным условием монотонности функция
) (см. рис. 3.5). Тогда в соответствии с достаточным условием монотонности функция  возрастает на интервале (
возрастает на интервале ( ) и убывает на интервале (
) и убывает на интервале (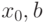 ).
).
По определению возрастающей функции  при всех
при всех  , а по определению убывающей функции
, а по определению убывающей функции  при всех
при всех  , т.е.
, т.е.  при всех
при всех  , следовательно,
, следовательно,  — точка максимума функции
— точка максимума функции 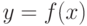 .
.
Аналогично рассматривается случай, когда производная меняет знак с минуса на плюс.
Отметим, что дифференцируемость функции в самой точке  не использовалась при доказательстве теоремы. На самом деле она и не требуется — достаточно, чтобы функция была непрерывна в точке
не использовалась при доказательстве теоремы. На самом деле она и не требуется — достаточно, чтобы функция была непрерывна в точке  .
.
Если изменение знака производной не происходит, то экстремума нет. Однако при работе с системами компьютерной математики удобнее второе достаточное условие экстремума.
3.4.1.4 Второе достаточное условие экстремума
Теорема. Если первая производная 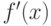 дважды дифференцируемой функции
дважды дифференцируемой функции 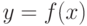 равна нулю в некоторой точке
равна нулю в некоторой точке  , а вторая производная в этой точке
, а вторая производная в этой точке 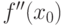 положительна, то
положительна, то  есть точка максимума функции
есть точка максимума функции 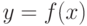 ; если
; если 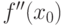 отрицательна, то
отрицательна, то  — точка максимума.
— точка максимума.
Пусть  , а f
, а f . Это значит, что
. Это значит, что

 , т.е.
, т.е. 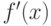 возрастает на некотором интервале
возрастает на некотором интервале  , содержащем точку
, содержащем точку  .
.Но  , следовательно, на интервале
, следовательно, на интервале  , а на интервале
, а на интервале  , т.е.
, т.е. 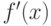 при переходе через точку
при переходе через точку  меняет знак с минуса на плюс, т.е.
меняет знак с минуса на плюс, т.е.  — точка минимума.
— точка минимума.
Аналогично рассматривается случай  и
и  .
.
Продолжим исследование функции

Как установлено выше, имеется одна критическая точка:  .
.
Задаёмся функцией 
(%i4) define(d2f(x),diff(df(x),x));
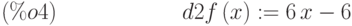
Вычисляем значение второй производной в критической точке:
(%i5) map(d2f,%o3);
![[6\,x-6=0]\leqno{(\%o5) }](/sites/default/files/tex_cache/8f85f9e860626c955444337f4c17c891.png)
В данном примере невозможно определить, является ли точка  экстремумом исследуемой функции, т.к. вторая производная в ней оказалась равной 0. Следует обратить внимание на способ вычисления — функция
экстремумом исследуемой функции, т.к. вторая производная в ней оказалась равной 0. Следует обратить внимание на способ вычисления — функция  применяется ко всем элементам списка, полученного при решении уравнения
применяется ко всем элементам списка, полученного при решении уравнения  (используется встроенная функция Maxima map).
(используется встроенная функция Maxima map).
Воспользуемся первым достаточным признаком наличия экстремума
(%i6) df(0);

(%i7) df(2);

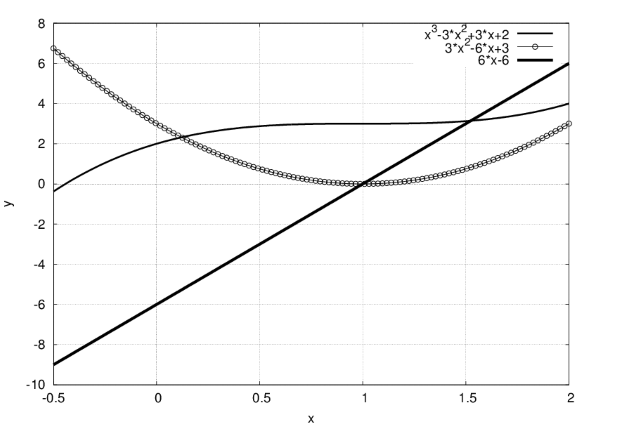
Как видно из приведенного результата, первая производная не изменяет знак в критической точке, что свидетельствует об отсутствии экстремума в ней.
Полученный результат иллюстрируется графиком исследуемой функции и её производных (см. рис. 3.6).
3.4.1.5 Схема исследования функции y = f(x) на экстремум
1. Найти производную  .
.
2. Найти критические точки функции, в которых производная  или не существует.
или не существует.
3.1. Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции.
Или
3.2. Найти вторую производную 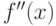 и определить ее знак в каждой критической точке.
и определить ее знак в каждой критической точке.
4. Найти экстремумы (экстремальные значения) функции.
Пример. Исследовать на экстремум функцию  .
.
1. y' = (x - 1)^3 + 3x(x - 1)^2 = (x - 1)^2(4x - 1).
2. Критические точки  и
и  .
.
3. Изменение знака производной при переходе через точку  не происходит, поэтому в этой точке нет экстремума.
не происходит, поэтому в этой точке нет экстремума.
![y'' = 2(x - 1)(4x - 1) + 4(x - 1)^2 = 2[(x - 1)(6x - 3)]](/sites/default/files/tex_cache/67e4e6fa1b4bb52818f5f91caa20abde.png) .
.
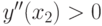 , поэтому в этой точке наблюдается минимум функции
, поэтому в этой точке наблюдается минимум функции  .
.
4.  .
.
Выполним тот же расчёт при помощи Maxima
(%i13) f(x):=x*(x-1)^3;

(%i14) define(df(x),diff(f(x),x));

(%i15) solve(df(x)=0,x);
![[x=\frac{1}{4},x=1]\leqno{(\%o15) }](/sites/default/files/tex_cache/e08e70578a1c56695904dd5655e8ec2c.png)
(%i16) define(d2f(x),diff(df(x),x));

(%i17) map(d2f,%o15);
![[6\,\left( x-1\right) \,x+6\,{\left( x-1\right) }^{2}=\frac{9}{4},6\,\left( x-1\right) \,x+6\,{\left( x-1\right) }^{2}=0]\leqno{(\%o17) }](/sites/default/files/tex_cache/42d774250fcb0e0e756e66513d7a76be.png)
В точке  вторая производная равна 0, поэтому вычисляем значения первой производной слева и справа от
вторая производная равна 0, поэтому вычисляем значения первой производной слева и справа от  :
:
(%i18) df(2);

(%i19) df(1/3);

Производная в окрестности точки  не меняет знак, поэтому экстремум у исследуемой функции один — точка
не меняет знак, поэтому экстремум у исследуемой функции один — точка  . Так как
. Так как  — точка минимума. Иллюстрация полученного результата — на рис. 3.7.
— точка минимума. Иллюстрация полученного результата — на рис. 3.7.
3.4.1.6 Нахождение наибольших и наименьших значений функции
Наибольшее или наименьшее значение функции на некотором отрезке может достигаться как в точках экстремума, так и в точках на концах отрезка.
Пусть функция 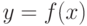 определена на некотором отрезке
определена на некотором отрезке ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
Нахождение наибольших и наименьших значений функций происходит по следующей схеме.
1. Найти производную 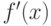 .
.
2. Найти критические точки функции, в которых  или не существует.
или не существует.
3. Найти значения функции в критических точках и на концах отрезка и выбрать из них наибольшее  и наименьшее
и наименьшее  значения. Это и будут наибольшее и наименьшее значение функции на исследуемом отрезке.
значения. Это и будут наибольшее и наименьшее значение функции на исследуемом отрезке.
Пример. Найти наибольшее и наименьшее значения функции  на отрезке [0, 3].
на отрезке [0, 3].
Аналитический расчёт:
1.  .
.
2. 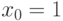 .
.
3.  .
.
В точке  наименьшее значение функции, а в точке
наименьшее значение функции, а в точке  — наибольшее.
— наибольшее.
Расчёт с использованием Maxima:
Находим критические точки исследуемой функции
(%i29) f(x):=3*x^2-6*x;

(%i30) define(df(x),diff(f(x),x));

(%i31) solve(df(x)=0,x);
![[x=1]\leqno{(\%o31) }](/sites/default/files/tex_cache/909dc47c3c2eadd4d5cd82e859dac622.png)
Результат расчёта — список, включающий один элемент (![[x = 1]](/sites/default/files/tex_cache/81b5d55db67ec07a38e9506cd0bafb5a.png) ).
).
Создаём новый список, включающий граничные значений и критические точки:
(%i32) L:[%o31[1],x=0,x=3];
![[x=1,x=0,x=3]\leqno{(\%o32) }](/sites/default/files/tex_cache/5e2d71c8627d6150454bf8186587fef0.png)
Применяем функцию  к каждому элементу списка
к каждому элементу списка  :
:
(%i33) map(f,L);
![[3\,{x}^{2}-6\,x=-3,3\,{x}^{2}-6\,x=0,3\,{x}^{2}-6\,x=9]\leqno{(\%o33) }](/sites/default/files/tex_cache/5748ac66be1b211965d04360c4787555.png)
Результат — наибольшие и наименьшие значения — находим в списке полученных значений.