Решение транспортных задач

Задача 3.3. Составление расписания занятий учебных групп

По учебному плану недельная нагрузка для учебной группы второго курса должна составлять 36 часов — по шесть учебных часов (или по три "пары") в день:

• математика 12 часов (6 пар);
• информатика 8 часов (4 пары);
• экономика 4 часа (2 пары);
• английский язык 4 часа (2 пары);
• бухгалтерия 4 часа (2 пары);
• делопроизводство 4 часа (2 пары).

Составить расписание занятий для двух групп на неделю так, чтобы в один день у каждой группы были по три разных дисциплины.

В данной задаче удобно при расчетах за единицу измерения выбрать сдвоенный учебный час, т.е. "пару", как это и делается при составлении расписаний на практике. Математическая модель должна включать в себя бинарную матрицу назначений. Число 1 обозначает, что занятие есть, а число 0 обозначает, что занятия нет.

В задаче нет нормативных коэффициентов, так как все занятия считаются одинаково ценными. Поэтому нужно просто сравнивать количество занятий с заданными ресурсами студентов и преподавателей. Ресурс студентов одинаков для всех дней недели и составляет три пары. Ресурс преподавателей для каждой группы определен учебным планом и изложен в условиях задачи.

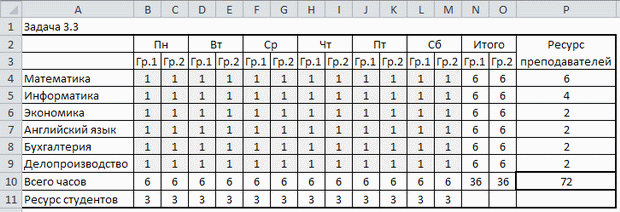
Обе группы рассмотрим в одной таблице, заполнив матрицу нормативных коэффициентов единицами:

В строке 10 суммируем число занятий студентов в день, а в столбцах N и O суммируем число занятий по дисциплинам по Гр.1 и Гр.2 соответственно. Целевую функцию помещаем в ячейку P10 как сумму ячеек N10 и O10.

В таблице присутствуют формулы автосуммы:

увеличить изображение

Десять столбцов скрыты, формулы в них аналогичны формулам в столбцах В и С.

Далее устанавливаем параметры "Поиска решения":

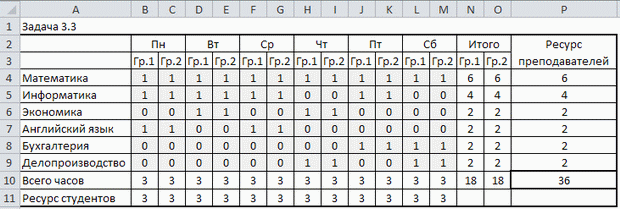
В результате поиска выдается одно из допустимых решений:

Данный процесс составления расписаний позволяет учитывать отдельные пожелания преподавателей. Например, преподаватель английского языка не может приходить по понедельникам. Тогда в параметры поиска решения вводим новое ограничение: В7:С7=0.

Ключевые термины

Закрытая модель — возможности поставщиков отправлять грузы совпадают с возможностями потребителей принять грузы (ресурсы поставщиков равны ресурсам потребителей).

Матрица назначений — матрица с бинарными коэффициентами. Коэффициент равен 1, если субъект назначен на объект , и равен 0 в противоположном случае.

Ресурс назначений — предельное число допустимых событий для субъекта или объекта.

Краткие итоги

В лекции рассмотрены методы оптимизации математических моделей транспортных задач. Несмотря на название "транспортные", математические модели этого типа охватывают многие задачи назначения и управления. В транспортных задачах используют, как правило, несколько матриц, в частности, бинарную матрицу назначений.

Вопросы

1. Какова общая структура транспортных моделей?
2. Как именуются пункты отправления?
3. Как именуются пункты назначения?
4. Можно ли именовать отправляемые грузы в пунктах отправления как предложение?
5. Можно ли именовать ожидаемые грузы в пунктах назначения как спрос?
6. Чем характеризуется закрытая модель?
7. Как формируется целевая функция в транспортных задачах?