Основные алгебраические структуры и операции
Произведение отображений
Определение 1.6.1.
Для диаграммы отображений
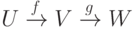
 отображений
отображений  и
и  следующим образом:
следующим образом: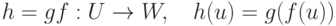
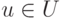 .
.Замечание 1.6.2.
Не любые два отображения можно перемножить!
Примеры 1.6.3.
- Если
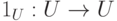 - тождественное отображение множества U,
- тождественное отображение множества U, 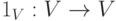 - тождественное отображение множества V,
- тождественное отображение множества V, 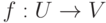 , то f1U=f=1Vf.
, то f1U=f=1Vf. - Если
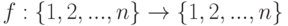 , f(k)=k+1 для
, f(k)=k+1 для 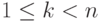 , f(n)=1, то fn=1U, где U={1,2,...,n}.
, f(n)=1, то fn=1U, где U={1,2,...,n}.
Теорема 1.6.4 (об ассоциативности произведения отображений).
Для диаграммы отображений 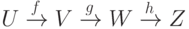 имеем h(gf)=(hg)f.
имеем h(gf)=(hg)f.
Доказательство. Ясно, что

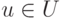 имеем (h(gf))(u)=h((gf)(u))=h(g(f(u))),
((hg)f)(u)=(hg)(f(u))=h(g(f(u))),
таким образом, (h(gf))(u)=((hg)f)(u) для всех
имеем (h(gf))(u)=h((gf)(u))=h(g(f(u))),
((hg)f)(u)=(hg)(f(u))=h(g(f(u))),
таким образом, (h(gf))(u)=((hg)f)(u) для всех 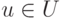 , следовательно, h(gf)=(hg)f.
, следовательно, h(gf)=(hg)f.Моноид отображений множества
Пусть U - множество, 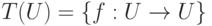 - совокупность всевозможных отображений с операцией произведения отображений. В силу доказанной теоремы 1.6.4 эта операция ассоциативна. Нейтральным элементом относительно этой операции является тождественное отображение 1U. Итак, T(U) - полугруппа с единицей, т. е. моноид.
- совокупность всевозможных отображений с операцией произведения отображений. В силу доказанной теоремы 1.6.4 эта операция ассоциативна. Нейтральным элементом относительно этой операции является тождественное отображение 1U. Итак, T(U) - полугруппа с единицей, т. е. моноид.
Задача 1.7.1.
Моноид отображений T(U) множества U коммутативен тогда и только тогда, когда |U|=1 (т. е. множество U состоит из одного элемента).
Указание
Если 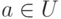 , то рассмотрим отображение
, то рассмотрим отображение 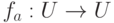 , fa(u)=a для всех
, fa(u)=a для всех 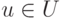 . Если
. Если 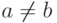 , то
, то 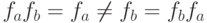 .
.

