|
Входит ли данный курс в перечень программы по переподготовки ФСТЭК? |
Измерение параметров элементов электрических и радиотехнических цепей
Общие сведения
Электрические и радиотехнические цепи с сосредоточенными постоянными состоят из резисторов, катушек индуктивности, конденсаторов и соединяющих проводов. Для отбора этих элементов или их проверки следует измерять активное, реактивное и полное сопротивления, индуктивность, емкость и взаимоиндуктивность. Кроме того, часто измеряют потери в конденсаторах и добротность катушек и колебательных контуров. Для этих измерений применяют методы вольтметра и амперметра, мостовой, резонансный метод и метод дискретного счета.
Метод вольтметра и амперметра
Метод вольтметра и амперметра – косвенный способ определения различных сопротивлений, позволяющий ставить элемент с определенным сопротивлением в рабочие условия. Этот метод основан на использовании закона Ома для участка цепи, сопротивление Rx которого определяется по известному падению напряжения Ux на нем и току Ix так:
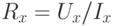 .
.
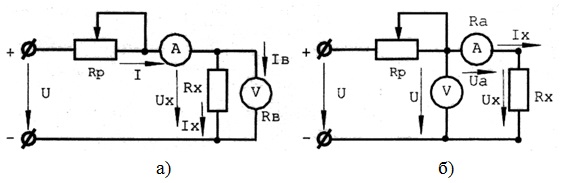
Существуют различные способы измерения падения напряжения Ux и тока Ix (рис. 7.1 рис. 7.1).
Ux и тока Ix
Измерительные части приведенных схем не обеспечивают одновременное измерение напряжения Ux и тока Ix. Так первая схема (рис. 7.1 а рис. 7.1) позволяет измерить с помощью вольтметра напряжение Ux. Амперметр дает возможность определить ток I, равный сумме Ix и Iв, из которой последний является током обмотки вольтметра. В этом случае определяемое сопротивление:
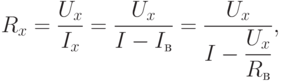
где Rв – сопротивление вольтметра.
Во второй схеме (рис. 7.1 б рис. 7.1) амперметр учитывает ток Ix, но вольтметр показывает напряжение U, равное сумме падений напряжений Ux на сопротивлении Rx и Ua на амперметре. Поэтому определяемое сопротивление:
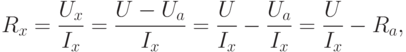
где Rа – сопротивление амперметра.
Следовательно, если при расчете определяемого сопротивления учитывать сопротивления приборов, то все схемы равноценны.
Если определяемое сопротивление Rx мало по сравнению с сопротивлением вольтметраRв, током Iв можно пренебречь и, применяя первую схему (рис. 7.1 а рис. 7.1), находить сопротивление Rx так:
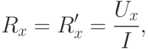
допуская относительную погрешность
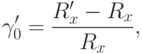
где  – измеренное значение сопротивления.
– измеренное значение сопротивления.
Учитывая, что  , имеем
, имеем
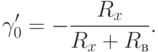
В случаях, когда определяемое сопротивление Rx сравнимо с сопротивлением вольтметраRв и пренебречь током Iв нельзя, следует пользоваться второй схемой (рис. 7.1 б рис. 7.1) и при расчете не учитывать падение напряжения Uа на амперметре, определяя сопротивление Rx так:
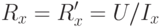
при относительной погрешности измерения
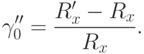
Учитывая, что 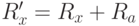 имеем
имеем
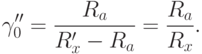
Для выявления пределов целесообразности использования той или другой схемы следует приравнять относительные погрешности, а затем найти значение сопротивления Rx, для которого обе схемы равноценны:
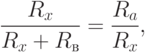
или

Откуда

Следовательно, для сопротивлений  предпочтительна схема (рис. 7.1 а
рис.
7.1), а для сопротивлений
предпочтительна схема (рис. 7.1 а
рис.
7.1), а для сопротивлений  схема (рис. 7.1 б
рис.
7.1). Первую из них называют схемой определения "малых" сопротивлений, а вторую – схемой для определения "больших" сопротивлений.
схема (рис. 7.1 б
рис.
7.1). Первую из них называют схемой определения "малых" сопротивлений, а вторую – схемой для определения "больших" сопротивлений.
При определении сопротивлений методом вольтметра и амперметра следует выбирать магнитоэлектрические приборы с такими пределами измерений, чтобы показания их были близки к номинальным значениям, т.к. это обеспечивает меньшие погрешности измерения.
Мостовой метод
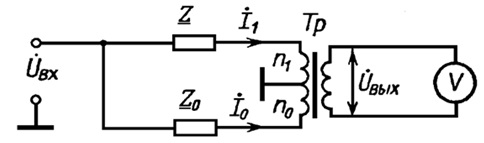
Основу мостового метода составляет принцип сравнения. Измеряемые активное и реактивное сопротивления сравнивают с сопротивлениями рабочих элементов, включенных в соответствующие плечи переменного тока (рис. 7.2 рис. 7.2).
Мост состоит из измеряемого  и
и  сопротивлений и трансформатора тока Тр. Особенность трансформатора тока – очень малые значения полных сопротивлений первичных обмоток. Поэтому через них токи определяются только сопротивлениями
сопротивлений и трансформатора тока Тр. Особенность трансформатора тока – очень малые значения полных сопротивлений первичных обмоток. Поэтому через них токи определяются только сопротивлениями  и
и  и не зависят от сопротивлений самих обмоток. Напряжение, возбуждаемое во вторичной обмотке, пропорционально магнитному потоку в сердечнике. Составляющие этого потока, создаваемые каждой из первичных обмоток, пропорциональны произведению тока обмотки на число ее витков (ампервитки) и имеют знаки, зависящие от направления витков. Первичные обмотки с числами витков n1 и n0 включены встречно; тогда создаваемые ими магнитные потоки противоположны. Равновесию моста соответствует условие компенсации этих потоков
и не зависят от сопротивлений самих обмоток. Напряжение, возбуждаемое во вторичной обмотке, пропорционально магнитному потоку в сердечнике. Составляющие этого потока, создаваемые каждой из первичных обмоток, пропорциональны произведению тока обмотки на число ее витков (ампервитки) и имеют знаки, зависящие от направления витков. Первичные обмотки с числами витков n1 и n0 включены встречно; тогда создаваемые ими магнитные потоки противоположны. Равновесию моста соответствует условие компенсации этих потоков
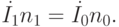 |
( 7.1) |
Состояние равновесия фиксируется по нулевым показаниям стрелочного прибора 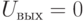 . В формуле (7.1)
. В формуле (7.1) 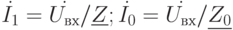 . Следовательно, при равновесии
. Следовательно, при равновесии

Трансформаторный мост можно уравновесить изменением обоих составляющих рабочего сопротивления и чисел витков в обмотках. Отношение чисел витков можно менять в больших пределах, оно стабильно во времени и при изменении температуры. Это определяет высокие метрологические характеристики трансформаторных мостов; отношение наибольшего значения измеряемой величины к наименьшему достигает 107; погрешность измерения в диапазоне звуковых частот может быть доведена до 0,01%.
Основным недостатком рассмотренной схемы является трудоемкий процесс уравновешивания моста. Разработаны автоматические мосты с цифровым отсчетом результата измерений. При этом в десятки раз уменьшается время измерения и повышается точность, появляется возможность построения автоматических измерительных систем. Наибольшее распространение получили автоматические трансформаторные мосты с преобразованием измеряемого и рабочего полных сопротивлений в пропорциональные им напряжения. Эти напряжения затем сравнивают и компенсируют. Соответствующая измерительная схема получила название автокомпенсационного моста.