|
Это в лекции 3. |
Три алгоритма на графах
Построение минимального остова
Во многих задачах в заданном графе нужно выделить некоторую часть, обладающую тем или иным свойством.
Определение 11.1. Граф G1=(V1,E1) называется подграфом графа G=(V,E), если  и
и 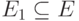 .
.
Для неориентированных связных графов одним из интересных классов подграфов являются деревья, сохраняющие связность вершин. Они называются остовами, остовными деревьями, каркасами или скелетами графа.
Определение 11.2. Остовом (неориентированного) связного графа G=(V,E) называется его подграф S=(V,T), являющийся деревом.
Пусть задана функция c: E -> R, приписывающая каждому ребру 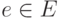 его стоимость (вес, длину)
его стоимость (вес, длину)  ( R - множество вещественных чисел).
Тогда стоимость c(S) дерева S определяется как сумма стоимостей всех его ребер, т.е.
( R - множество вещественных чисел).
Тогда стоимость c(S) дерева S определяется как сумма стоимостей всех его ребер, т.е. 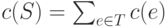 .
.
Минимальным остовом называется остов минимальной стоимости.
Таким образом, минимальный остов - это самая дешевая (короткая) система путей, связывающая все вершины G.
Опишем процедуру построения минимального остова, предложенную Дж. Крускалом в 1956г.
Вход: связный граф G=(V,E) и функция стоимости ребер c: E -> R.
Выход: минимальный остов S=(V,T).
Этап 1. Пусть E содержит m ребер. Упорядочим их по возрастанию стоимостей:

Этап 2. Последовательно для каждого i =1, ... , m определим множество ребер Ti:
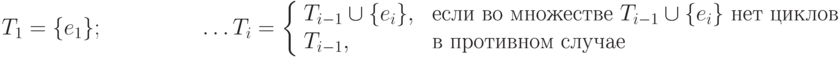
Положим T=Tm.
Выдать в качестве результата граф S=(V,T).
Докажем, что этот алгоритм корректен.
Теорема 11.1. Алгоритм МинОстов строит минимальный остов входного графа G=(V,E).
Доказательство Пусть результатом работы МинОстов на графе G=(V,E)
является граф S=(V,T). Отметим вначале, что S является деревом.
Действительно, отсутствие циклов следует из определения множеств Ti.
Предположим, что S не является связным. Тогда должны существовать
две вершины  , которые не достижимы друг из друга в S.
Но граф G связен, поэтому в нем есть путь из u в v. Тогда на этом пути обязательно имеется такое ребро
, которые не достижимы друг из друга в S.
Но граф G связен, поэтому в нем есть путь из u в v. Тогда на этом пути обязательно имеется такое ребро  , у которого один конец a соединен путем с u в графе S, а второй конец b - нет. Но тогда на шаге i ребро ei должно попасть в Ti, так как его добавление не образует цикла. Следовательно, граф S связен.
, у которого один конец a соединен путем с u в графе S, а второй конец b - нет. Но тогда на шаге i ребро ei должно попасть в Ti, так как его добавление не образует цикла. Следовательно, граф S связен.
Покажем теперь, что дерево S имеет минимальную стоимость. Пусть T={d1, ...,dk, ..., dn-1} - упорядочение всех ребер T по стоимости.
Покажем индукцией по k=1, ... , (n-1), что существует минимальный остов, включающий ребра d1, ...,dk.
Пусть S'=(V,T') - минимальный остов, у которого (k-1) наименьших по стоимости ребер совпадают с ребрами T, т.е. упорядочение всех его ребер имеет вид: T'={f1=d1, ..., fk-1= dk-1, fk, ..., fn-1} и  .
Пусть dk=(u,v). В T' имеется некоторый путь p из u в v,
который не содержит ребро dk. На этом пути обязательно есть некоторое ребро f=(u''),
не попавшее в T, иначе в T
образовался бы цикл. Из построения T следует, что c(dk) <= c(f).
Рассмотрим граф
.
Пусть dk=(u,v). В T' имеется некоторый путь p из u в v,
который не содержит ребро dk. На этом пути обязательно есть некоторое ребро f=(u''),
не попавшее в T, иначе в T
образовался бы цикл. Из построения T следует, что c(dk) <= c(f).
Рассмотрим граф 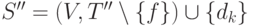 .
Очевидно, что этот граф является остовным деревом. Действительно,
связь между u' и v' сохранилась, так как в S'' имеется путь:
.
Очевидно, что этот граф является остовным деревом. Действительно,
связь между u' и v' сохранилась, так как в S'' имеется путь: 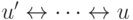
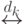
 .
Поэтому S'' - связный граф. Если бы в S'' был цикл, то он обязательно
включал бы ребро dk. Но тогда часть этого цикла без ребра dk
образовывала бы путь p' между u в v, не совпадающий с путем p. Следовательно, в дереве T' было бы два разных пути
между u в v, что невозможно, так как тогда в T' был бы цикл.
Отсюда заключаем, что в S'' циклов нет и S'' - остовное дерево.
Его стоимость c(S'')= c(S') - c(f) + c(dk) <= c(S'). Так как S' - минимальный остов,
то c(S'')=c(S') и S'' - тоже минимальный остов, у которого с S
имеется k общих ребер: d1, ..., dk.
.
Поэтому S'' - связный граф. Если бы в S'' был цикл, то он обязательно
включал бы ребро dk. Но тогда часть этого цикла без ребра dk
образовывала бы путь p' между u в v, не совпадающий с путем p. Следовательно, в дереве T' было бы два разных пути
между u в v, что невозможно, так как тогда в T' был бы цикл.
Отсюда заключаем, что в S'' циклов нет и S'' - остовное дерево.
Его стоимость c(S'')= c(S') - c(f) + c(dk) <= c(S'). Так как S' - минимальный остов,
то c(S'')=c(S') и S'' - тоже минимальный остов, у которого с S
имеется k общих ребер: d1, ..., dk.
Тогда при k=n-1 получаем, что S - минимальный остов.
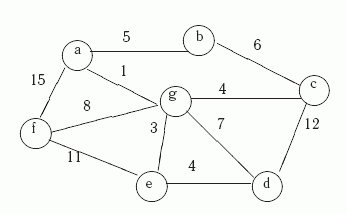
Пример 11.1. Рассмотрим нагруженный граф G, показанный на рис. 11.1.
Применим к нему алгоритм МинОстов. На первом этапе упорядочим все ребра, а на втором - рядом с каждым из них определим соответствующее множество Ti. Ребра, попавшие в T, будем по ходу вычисления отмечать знаком '+', а не попавшие - знаком '-'.
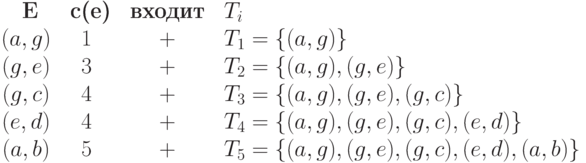
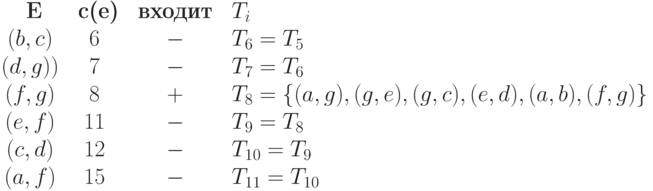
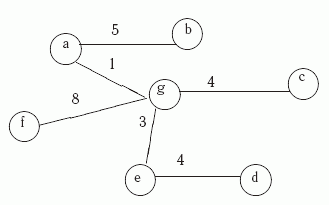
Таким образом, мы построили для G минимальный остов S=(V,T), где T=T8 ={ (a,g), (g,e), (g,c), (e,d), (a,b), (f,g)}. Он показан на рис. 11.2. Стоимость этого остова c(S)=25.
Замечание. Так как дерево с n вершинами содержит в точности (n-1) ребер, то работу алгоритма МинОстов можно прекращать после такого шага i, на котором в Ti окажется |V| - 1 ребер. В нашем примере |V| =7 и алгоритм мог остановиться после 8-го шага.