|
Это в лекции 3. |
Булевы функции и их представления
Задачи
Задача 3.1. Какие подмножества вершин B4 соответствуют следующим булевым функциям:
-
 ;
; -
 ;
; -
 (здесь + - арифметическое сложение);
(здесь + - арифметическое сложение); -
 или x3x4 = 1
.
или x3x4 = 1
.
Задача 3.2. Построить таблицы значений для следующих булевых функций:
-
 ;
; -
 сумма (X1 +X2 + X3)
четна;
сумма (X1 +X2 + X3)
четна; -
 значение X1 совпадает со значением X2 или со значением X3.
значение X1 совпадает со значением X2 или со значением X3. - f4(X1,X2,X3) = если X1=1 , то X2 , иначе X3 .
Задача 3.3. Построить таблицы для функций, задаваемых следующими формулами:
 ;
;
 ;
;
 .
.
Задача 3.4. Назовем два набора  и
и  соседними}, если они находятся в соседних строках таблицы для функции от n переменных, т.е. представляют двоичные записи чисел
соседними}, если они находятся в соседних строках таблицы для функции от n переменных, т.е. представляют двоичные записи чисел  и
и  , для которых
, для которых 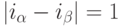 .
.
Найти число функций в  , которые на любой паре
соседних наборов принимают
, которые на любой паре
соседних наборов принимают
- одинаковые значения;
- разные значения.
Задача 3.5. Назовем два набора  и
и  противоположными}, если для всякого i
противоположными}, если для всякого i  (и, следовательно,
(и, следовательно,  ).
).
Найти число функций в  , которые на любой паре
противоположных наборов принимают разные значения.
, которые на любой паре
противоположных наборов принимают разные значения.
Задача 3.6. Пусть n =2k. Назовем набор  парным,} если для любого i=1, ..., k
парным,} если для любого i=1, ..., k  ,т.е.
,т.е.  для некоторого набора
для некоторого набора  размера k.
размера k.
Найти число функций в 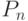 , которые на всех парных
Наборах принимают одинаковое значение.
, которые на всех парных
Наборах принимают одинаковое значение.
Задача 3.7. Администратор базы данных обнаружил, что одна или несколько из трех записей его базы A, B и C ошибочна. Он установил, что
- если запись B корректна, то A ошибочна;
- хотя бы одна запись из пары B, C корректна и хотя бы одна запись из пары A, C корректна;
- если A ошибочна, то хотя одна из записей B, C корректна (но не обе вместе).
Опишите знания администратора в виде булевой формулы. Может ли он сделать вывод, что запись B ошибочна? Можно ли достоверно утверждать, что ошибочная запись единственна?
Задача 3.8. Программист Петр использовал в своей программе три целочисленные переменные x, y и z. В определенном месте программы он поместил условный оператор:
IF (x*y >= 0)OR (x*z >= 0) THEN x=1 ELSE x=2;
Проанализировав свою программу, Петр установил, что перед выполнением этого Оператора выполнены следующие условия:
- если z < 0, то x < 0 или y >= 0 ;
- x >= 0 или y < 0 ;
- если y < 0, то хотя бы одна из переменных x, z отрицательна, но не обе вместе.
Опишите знания Петра в виде булевой формулы. Может ли он оптимизировать программу, заменив указанный условный оператор на присвоение x=1 или на присвоение x=2? Если "да", то на какое?
Задача 3.9. Комитет состоит из пяти членов. Решения принимаются большинством
голосов,
однако, если председатель голосует "против", то решение не принимается.
Постройте формулу, зависящую от 5 переменных X1, X2,X3, X4, Y
(  -ый член комитета голосует "за",
-ый член комитета голосует "за",  председатель "за"),
значение которой равно 1 тогда и только тогда, когда в результате голосования
решение принимается.
председатель "за"),
значение которой равно 1 тогда и только тогда, когда в результате голосования
решение принимается.
