Графика
3.3. Трехмерные графики
При задании функции двух переменных, любой паре чисел (x,y) из некоторого множества D упорядоченных пар чисел поставлено в соответствие по определенному закону единственное число – значение функции F(x,y). Множество D называется областью определения функции. Пару чисел x,y можно рассматривать как пару координат точки M на плоскости, координата z=F(x,y) . При этом аргументами функции будут координаты x,y точки M. Числа x,y можно рассматривать как координаты вектора r , исходящего из начала координат и с концом в точке M(x,y). Тогда функция двух переменных будет функцией вектора, что записывается в виде формулы z = F(r), причем аргументами функции являются координаты вектора r .
3.3.1.График поверхности
График функции двух переменных есть множество точек (x,y, F(x,y)). График представляет собой некоторую поверхность. График функции двух переменных F(x,y) строится с использованием шаблона графика поверхности на панели Графика. Для построения графика поверхности можно использовать различные способы [3]. Если надо только посмотреть общий вид поверхности, MathCAD автоматически строит график.
Для построения графика:
- определить математически функцию двух переменных
- Вызвать Surface Plot с панели графиков (или команду Insert -> Graph -> Surface Plot
- В графической области на месте шаблона для ввода указать (без аргументов) имя функции F.
При автоматическом построении графика независимые переменные x и y принимают значения из промежутка [-5,5].
Пример 3.9
Построим график функции  (Рис.3.19).
(Рис.3.19).

Настройка графика (изменение параметров)
Чтобы изменить заданные по умолчанию параметры графиков, надо выделить график и, активизировать двойным щелчком левой кнопкой мыши. Появится диалоговое окно 3-D Plot Format (Форматирование трехмерных графиков) (Рис.3.20).
Диалоговое окно 3-D Plot Format содержит девять закладок и множество флажков для выбора режима построения графика.
Вкладка General "Общее".
Раздел View "Вид" показывает углы, под которыми наблюдается построенный график поверхности.
Поле Rotation определяет угол поворота вокруг оси Z в плоскости X-Y. Значение в поле Tilt задает угол наклона линии взгляда к плоскости X-Y. Поле Zoom позволяет увеличить (уменьшить) графическое изображение в число раз, равное цифре, указанной в поле.
Раздел "Стиль оси" определяет стиль изображения размеров графика:
- периметр –график с размерами по периметру;
- угол –график с размерами по осям;
- нет –график без размеров по периметру и по осям;
- равные шкалы – установка по осям равных масштабов.
Раздел Frames (Границы) определяет обрамление графика:
- Show border – показывает границы графика;
- Show box каркас – показывает график в параллепипеде.
- Plot 1 Display as (График/ несколько графиков Отобразить как) График 1 Панель переключателей определяет форму представления трехмерного графика: контурный, точечный, векторное поле и др.)
После изменения параметра щелкните по кнопке Применить. Для возвращения в документ нажмите клавишу ОК.
Вкладка Axes (Ось) позволяет изменять внешний вид осей координат
- Grids (Сетки) - можно отобразить на графике линии, описываемые уравнениями x,y,z= const.
- Если переменные введены с индексами –
 ,
, 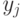 на осях Ox и Oy указываются значения индексов i и j, в то время как ось Oz размечается в соответствии с промежутком, которому принадлежат элементы матрицы значений
на осях Ox и Oy указываются значения индексов i и j, в то время как ось Oz размечается в соответствии с промежутком, которому принадлежат элементы матрицы значений 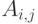 .
. - Auto Grid (Автосетка), программа самостоятельно задает сетку. Если ее отключить, можног указать число линий сетки,.
- Auto Scale (Авошкала) , MathCAD сам определяет границы построения графика и масштабы по осям.
- При отключении Auto Scale можно самостоятельно задать пределы изменения переменных в полях Minimum Value(Минимум) и Maximum Value (Максимум).
- Show Numbers (Нумерация), отображаются метки на осях и подписи к ним.
На вкладке QuickPlot Data (Рис.3.21) можно установить другие пределы изменения независимых переменных x и y, установить количество линий сетки, определить систему координат: декартову, сферическую, цилиндрическую.
Для представления графика в разных системах координат достаточно щелкнуть соответствующий переключатель Coordinat System (Рис.3.21). На рисунках 3.22 и Рис.3.23 показаны графики функции примера 3.9. в сферической и цилиндрической системе координат


Вкладка Appearance (Внешний вид) позволяет изменять для каждого графика вид и цвет заливки поверхности (область Fill Options); вид, цвет и толщину дополнительных линий на графике (область Line Options); наносить на график точки данных (опция Draw Points области Point Options), менять их вид, размер и цвет.
Важная опция Calomap окрашивает график: максимальные значения в красный, наименьшие – в синий цвет как в спектре видимого света..
Вкладка Lighting (Освещение). При включении опции Enable Lighting (Наличие подсветки) позволяет выбрать цветовую схему для освещения, "установить" несколько источников света, выбрав для них цвет освещения и определив его направление.
Вкладка Backplanes (Основание) позволяет изменить внешний вид плоскостей, ограничивающих область построения: цвет, нанесение сетки, определение ее цвета и толщины, прорисовка границ плоскостей
Вкладка Advansed (Дополнительно)позволяет установить параметры печати и изменить цветовую схему для окрашивания поверхности нрафика, а также указать направление смены окраски (вдоль оси Ox, Oy или Oz). Включение опции Enable Fog (Наличие Тумана) делает график нечетким, слегка размытым (полупрозрачным). При включении опции Perspective (Перспектива) появляется возможность указать в соответствующем поле расстояние до наблюдателя.
Примеры построения графиков функций
В автоматическом режиме (по умолчанию) MathCAD строит график в интервале изменения переменных x и y: (-5;5). Если в этой области функция не является непрерывной (имеет разрыв), график не строится. Можно перестроить пределы изменения x и y в окне форматирования. Можно задать пределы изменения x и y аналитически, в нужной области рассмотрения графика и построить сетку с нужными параметрами. Рассмотрим построение графиков различными способами.
Пример 3.10
Построить график поверхности функции ![F(x,y)=\ln{[(x-8)(y-10)]}](/sites/default/files/tex_cache/69e9c57494b9dc9f105d8385ac1b4e5f.png) разными способами.
разными способами.
1 способ. "Быстрый" график" (Рис.3.24).
Для построения графика:
- функция определена
- вызвать Graph -> Surface Plot
- на месте шаблона указать имя функции F.
![F(x,y):=\ln[(x-8)(y-10)]](/sites/default/files/tex_cache/0e010b7c209aaddc9d29525a7f40f390.png)
2 способ. Использование сетки. Построить график ![W(x,y)=\ln{[(x-8)(y-10)]}](/sites/default/files/tex_cache/6b37f468cb179801e07670b415152db7.png) Fпо 20 точкам. Переменная x меняется от 8 д и о 10 , y меняется, от 10 до 12.
Fпо 20 точкам. Переменная x меняется от 8 д и о 10 , y меняется, от 10 до 12.
Для построения графика в определенной области изменения независимых переменных с определенным шагом надо задать узловые точки  ,
, 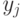 , как индексные переменные по точкам. Затем сформировать матрицу значений функции в точках в виде:
, как индексные переменные по точкам. Затем сформировать матрицу значений функции в точках в виде:  .
.
- Задать количество точек.
- Ввести номер точки i номер точки j как ранжированные переменные.
- Задать пределы для x y. Задать
 и
и 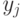 как индексные переменные по сетке.
как индексные переменные по сетке. - Определить матрицу
 .
. - Вставить график, на месте шаблона вставить имя матрицы (Рис.3.24).
График строится не от значений x и y, а от номера точки.
![W(x,y):=\ln[(x-8)(y-10)]](/sites/default/files/tex_cache/0fdde979008294565c4bce2e6b0e35ad.png)
 ,
, 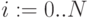 ,
, 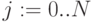
 ,
,  ,
, 
 ,
,  ,
, 

Значение функции  в крайних точках сетки:
в крайних точках сетки:
 ,
, 
 ,
, 







