Микросхемы и их функционирование
В табл. 2.4 приведены примеры 16-ричного кодирования первых 20 чисел (в скобках приведены двоичные числа), а на рис. 2.10 показан пример записи двоичного числа в 16-ричном виде. Для обозначения 16-ричного кодирования иногда применяют букву "h" или "H" (от английского Hexadecimal) в конце числа, например, запись A17F h обозначает 16-ричное число A17F. Здесь А1 представляет собой старший байт числа, а 7F — младший байт числа. Все число (в нашем случае — двухбайтовое) называется словом.
| Десятичная система | 16-ричная система | Десятичная система | 16-ричная система |
|---|---|---|---|
| 0 | 0 (0000) | 10 | A (1010) |
| 1 | 1(0001) | 11 | B (1011) |
| 2 | 2 (0010) | 12 | C (1100) |
| 3 | 3 (0011) | 13 | D (1101) |
| 4 | 4 (0100) | 14 | E (1110) |
| 5 | 5 (0101) | 15 | F (1111) |
| 6 | 6 (0110) | 16 | 10 (00010000) |
| 7 | 7 (0111) | 17 | 11 (00010001) |
| 8 | 8 (1000) | 18 | 12 (00010010) |
| 9 | 9 (1001) | 19 | 13 (00010011) |
Для перевода 16-ричного числа в десятичное необходимо умножить значение младшего (нулевого) разряда на единицу, значение следующего (первого) разряда на 16, второго разряда на 256 (162) и т.д., а затем сложить все произведения. Например, возьмем число A17F:
A17F=F*160 + 7*161 + 1*162 + A*163 = 15*1 + 7*16+1*256+10*4096=41343
| Десятичная система | 8-ричная система | Десятичная система | 8-ричная система |
|---|---|---|---|
| 0 | 0 (000) | 10 | 12 (001010) |
| 1 | 1(001) | 11 | 13 (001011) |
| 2 | 2 (010) | 12 | 14 (001100) |
| 3 | 3 (011) | 13 | 15 (001101) |
| 4 | 4 (100) | 14 | 16 (001110) |
| 5 | 5 (101) | 15 | 17 (001111) |
| 6 | 6 (110) | 16 | 20 (010000) |
| 7 | 7 (111) | 17 | 21 (010001) |
| 8 | 10 (001000) | 18 | 22 (010010) |
| 9 | 11 (001001) | 19 | 23 (010011) |
Но каждому специалисту по цифровой аппаратуре (разработчику, оператору, ремонтнику, программисту и т.д.) необходимо научиться так же свободно обращаться с 16-ричной и двоичной системами, как и с обычной десятичной, чтобы никаких переводов из системы в систему не требовалось.
Значительно реже, чем 16-ричное, используется восьмеричное кодирование, которое строится по такому же принципу, что и 16-ричное, но двоичные разряды разбиваются на группы по три разряда. Каждая группа (разряд кода) затем обозначается одним символом. Каждый разряд 8-ричного кода может принимать восемь значений: 0, 1, 2, 3, 4, 5, 6, 7 (табл. 2.5).
Помимо рассмотренных кодов, существует также и так называемое двоично-десятичное представление чисел. Как и в 16-ричном коде, в двоично-десятичном коде каждому разряду кода соответствует четыре двоичных разряда, однако каждая группа из четырех двоичных разрядов может принимать не шестнадцать, а только десять значений, кодируемых символами 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. То есть одному десятичному разряду соответствует четыре двоичных. В результате получается, что написание чисел в двоично-десятичном коде ничем не отличается от написания в обычном десятичном коде (табл. 2.6), но в реальности это всего лишь специальный двоичный код, каждый разряд которого может принимать только два значения: 0 и 1. Двоично-десятичный код иногда очень удобен для организации десятичных цифровых индикаторов и табло.
| Десятичная система | Двоично-десятичная система | Десятичная система | Двоично-десятичная система |
|---|---|---|---|
| 0 | 0 (0000) | 10 | 10 (00010000) |
| 1 | 1(0001) | 11 | 11 (00010001) |
| 2 | 2 (0010) | 12 | 12 (00010010) |
| 3 | 3 (0011) | 13 | 13 (00010011) |
| 4 | 4 (0100) | 14 | 14 (00010100) |
| 5 | 5 (0101) | 15 | 15 (00010101) |
| 6 | 6 (0110) | 16 | 16 (00010110) |
| 7 | 7 (0111) | 17 | 17 (00010111) |
| 8 | 8 (1000) | 18 | 18 (00011000) |
| 9 | 9 (1001) | 19 | 19 (00011001) |
В двоичном коде над числами можно проделывать любые арифметические операции: сложение, вычитание, умножение, деление.
Рассмотрим, например, сложение двух 4-разрядных двоичных чисел. Пусть надо сложить число 0111 (десятичное 7) и 1011 (десятичное 11). Сложение этих чисел не сложнее, чем в десятичном представлении:

При сложении 0 и 0 получаем 0, при сложении 1 и 0 получаем 1, при сложении 1 и 1 получаем 0 и перенос в следующий разряд 1. Результат — 10010 (десятичное 18). При сложении любых двух n-разрядных двоичных чисел может получиться n-разрядное или (n+1) -разрядное число.
Точно так же производится вычитание. Пусть из числа 10010 (18) надо вычесть число 0111 (7). Записываем числа с выравниванием по младшему разряду и вычитаем точно так же, как в случае десятичной системы:

При вычитании 0 из 0 получаем 0, при вычитании 0 из 1 получаем 1, при вычитании 1 из 1 получаем 0, при вычитании 1 из 0 получаем 1 и заем 1 в следующем разряде. Результат — 1011 (десятичное 11).
При вычитании возможно получение отрицательных чисел, поэтому необходимо использовать двоичное представление отрицательных чисел.
Для одновременного представления как двоичных положительных, так и двоичных отрицательных чисел чаще всего используется так называемый дополнительный код. Отрицательные числа в этом коде выражаются таким числом, которое, будучи сложено с положительным числом такой же величины, даст в результате нуль. Для того чтобы получить отрицательное число, надо поменять все биты такого же положительного числа на противоположные (0 на 1, 1 на 0) и прибавить к результату 1. Например, запишем число –5. Число 5 в двоичном коде выглядит 0101. Заменяем биты на противоположные: 1010 и прибавляем единицу: 1011. Суммируем результат с исходным числом: 1011 + 0101 = 0000 (перенос в пятый разряд игнорируем).
Помимо стандартных арифметических операций, в двоичной системе счисления используются и некоторые
специфические операции, например, сложение по модулю 2. Эта операция (обозначается A) является побитовой,
то есть никаких переносов из разряда в разряд и заемов в старших разрядах здесь не существует. Правила сложения по
модулю 2 следующие: 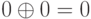 ,
, 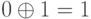 ,
,  ,
, 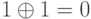 . Эта же операция называется функцией Исключающее ИЛИ. Например, просуммируем по модулю 2 два двоичных числа 0111 и 1011:
. Эта же операция называется функцией Исключающее ИЛИ. Например, просуммируем по модулю 2 два двоичных числа 0111 и 1011:

Среди других побитовых операций над двоичными числами можно отметить функцию И и функцию ИЛИ. Функция И дает в результате единицу только тогда, когда в соответствующих битах двух исходных чисел обе единицы, в противном случае результат —0. Функция ИЛИ дает в результате единицу тогда, когда хотя бы один из соответствующих битов исходных чисел равен 1, в противном случае результат 0.
