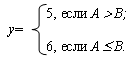Кодирование команд (часть 3)
Пример 2.
MUL [BX]
Умножение без знака содержимого AL на операнд, адрес которого задан в команде. Операнд находится в памяти.
Время вычисления EA (регистровая косвенная адресация): 5 тактов.
Т=(76...83)+5 = (81...88) тактов = (810...880) нс
Пример 3.
JZ MET ; перейти на MET, если "ноль"
Базовое время: 4 такта, если нет перехода, и 16 тактов, если переход выполняется.
Других затрат времени нет.
Т=4 такта=40 нс перехода нет. Т=16 тактов=160 нс переход выполняется.
Пример 4.
JMP dword ptr [SI+15] ; межсегментный косвенный переход.
Время вычисления EA (регистровая относительная адресация): 9 тактов.
Имеются 2 обращения к памяти за новыми значениями IP и CS.
Т=24+9=33 (такта)=330 (нс).
Т=24+9+2*4=41 (такт)=410 (нс).
Время выполнения линейного участка программы равно сумме времен выполнения всех команд этого участка.
Оценим время выполнения ветвящейся программы на примере следующей задачи:
Ниже представлен текст соответствующей программы в предположении, что A, B и y - переменные длиной 1 байт, имеющие идентификаторы MA, MB и MY соответственно. Здесь и далее полагаем, что используемые адреса в сегменте данных - четные. Рядом с каждой командой указано количество тактов синхронизации, необходимое для ее выполнения (идентификаторы соответствуют прямому режиму адресации ):
MOV BL,5 ; 4
MOV AL,MA ; 10
CMP AL,MB ; 15
JG OUT ; 4/16
INC BL ; 3
OUT: MOV MY,BL ; 15Таким образом, если A>B, то программа выполняется за 60 тактов, в противном случае - за 51 такт.
Если оба случая равновероятны, то
Тср = (Т1+Т2)/2 = 55.5 (такта).
В общем случае для данной программы
Тср = 4+10+15+16*p1+(4+3)*p2+15=44+16*p1+7*p2.
где p1 и p2 - вероятности перехода в команде JG в случае выполнения и невыполнения условия соответственно ( p1+p2=1 ).
Если известна количественная или хотя бы качественная оценка соотношения p1 и p2, то можно минимизировать среднее время выполнения данного фрагмента программы.
Пусть известно, что A>B при 90% различных исходных данных. Тогда для рассмотренной программы:
Тср = 44+0.9*16+0.1*7=59.1 (такта).
При обратном соотношении, то есть при p1=0.1:
Тср = 44+0.1*16+0.9*7=51.9 (такта).
Следовательно, при p1=0.1 быстрее будет выполняться программа, меняющая условие перехода:
MOV BL,6 ; 4
MOV AL,MA ; 10
CMP AL,MB ; 15
JNG OUT ; 4/16
DEC BL ; 3
OUT: MOV MY,BL ; 15Она дает то же самое среднее время выполнения программы при p1=p2, но выигрыш при p1>p2 и проигрыш при p1<p2.
В циклических программах тело цикла выполняется многократно. В силу этого целесообразно, по возможности, минимизировать этот участок программы даже за счет увеличения времени выполнения подготовительных операций и операций обработки результатов циклического участка.
Рассмотрим это положение на следующем примере. Пусть необходимо вычислить произведение двух целых положительных чисел длиной в слово ( S=M*N ), не используя команду умножения. Предполагаем, что операнды располагаются в памяти по эффективным адресам, вычисляемым как [SI+2A] и [1148h], а результат также не превышает одного слова и должен быть записан в память по адресу [BX+SI]. Предполагаем также, что все адреса в сегменте данных четные.
Решать задачу будем по следующей схеме:
Рассмотрим несколько возможных вариантов решения.
Вариант 1.
MOV [BX+SI],0 ; 17
MOV AX,[1148h] ; 10
CYCLE: ADD [BX+SI],AX ; 23
DEC [SI+2A] ; 24
JNZ CYCLE ; 4/16Вариант 2.
MOV AX,[1148h] ; 10
MOV CX,[SI+2A] ; 17
SUB DX,DX ; 3
CYCLE: ADD DX,AX ; 3
DEC CX ; 2
JNZ CYCLE ; 4/16
MOV [BX+SI],DX ; 16Вариант 3.
MOV AX,[1148h] ; 10
MOV CX,[SI+2A] ; 17
SUB DX,DX ; 3
CYCLE: ADD DX,AX ; 3
LOOP CYCLE ; 15/17
MOV [BX+SI],DX ; 16Вариант 1 использует минимальное общее количество команд. В варианте 2 обработка идет в регистрах общего назначения, но не используется специальная команда цикла, которая использована в варианте 3.
Сравнительные характеристики этих вариантов представлены в табл. 9.3
| Вариант | Количество команд | Длина программы, (байт) | Время выполнения, (такт) |
|---|---|---|---|
| 1 | 5 | 14 | 63N+15 |
| 2 | 7 | 15 | 21N+34 |
| 3 | 6 | 14 | 20N+34 |
Таким образом, даже несмотря на некоторое увеличение длины, программа, реализованная в вариантах 2 и 3, при достаточно больших N выполняется почти втрое быстрее, чем реализованная в варианте 1.
Так как время выполнения этих программ зависит от величины лишь одного сомножителя, то в том случае, когда известны относительные величины сомножителей, это время можно минимизировать, используя в качестве счетчика наименьший из сомножителей.