Функциональные узлы комбинаторной логики. Дешифраторы
Дешифратор является частным случаем преобразователей произвольных кодов, рассмотренных в "Преобразователи произвольных кодов" .
Дешифратор - это логическая схема, преобразующая двоичный код в унарный, когда только на одном из всех выходов появляется активный сигнал. Номер этого активного выхода в десятичном коде совпадает с двоичным кодом, подаваемым на входные линии дешифратора.
Принцип действия дешифратора лежит в основе работы всем известного устройства - домофона. Когда мы набираем номер на домофоне, звонок звенит только в одной квартире с указанным номером.
Рассмотрим схему дешифратора на три входа. Как при синтезе логической схемы по арифметическому выражению (
"Преобразователи произвольных кодов"
), составляем таблицу истинности. Поскольку в нашем примере у схемы должно быть три входа, количество комбинаций на этих входах будет равно 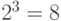 , поэтому выходов у схемы будет также 8. Обозначим входные сигналы переменной
, поэтому выходов у схемы будет также 8. Обозначим входные сигналы переменной  с индексом, соответствующим весу двоичного разряда - 1, 2, 4 (табл. 4.1). Выходные сигналы обозначим как
с индексом, соответствующим весу двоичного разряда - 1, 2, 4 (табл. 4.1). Выходные сигналы обозначим как  с индексом, соответствующим поданному на входы двоичному коду, при котором этот выход активен. Для синтезируемой схемы примем положительную логику, когда активным является уровень логической 1.
с индексом, соответствующим поданному на входы двоичному коду, при котором этот выход активен. Для синтезируемой схемы примем положительную логику, когда активным является уровень логической 1.
| Входные сигналы | Выходные сигналы | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
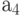 |
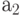 |
 |
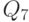 |
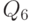 |
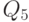 |
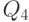 |
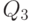 |
 |
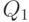 |
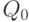 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
В соответствии с принципом синтеза логических схем по заданной формуле, после составления таблицы истинности нужно для каждого выхода написать логическое выражение. В данном случае задача упрощается, так как для каждого выхода логическая 1 имеет место быть только в одной строке таблицы. Поэтому в логическом выражении для каждого выхода будет только один минтерм:
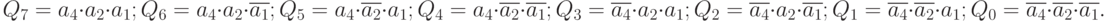 |
( 4.1) |
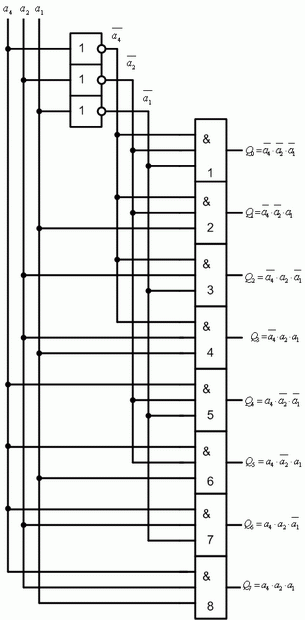
На рис. 4.1 показана функциональная схема данного дешифратора, соответствующая логическим выражениям (4.1).
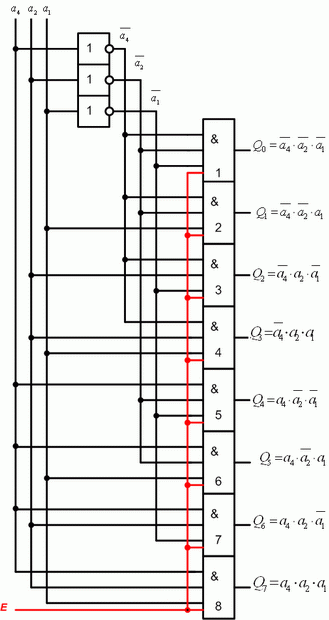
В реальных дешифраторах обязательно присутствует входной управляющий сигнал, разрешающий работу данного дешифратора в соответствии со своей функцией. В простейшем случае разрешающий сигнал  (от англ. enable - давать возможность) может подаваться на каждый из логических элементов И, осуществляющих вычисление по (4.1), так, как показано на рис. 4.2 красным цветом. Если
(от англ. enable - давать возможность) может подаваться на каждый из логических элементов И, осуществляющих вычисление по (4.1), так, как показано на рис. 4.2 красным цветом. Если  , то он не влияет на работу схемы (рис. 4.2). Дешифратор работает так, как описано выше. Если
, то он не влияет на работу схемы (рис. 4.2). Дешифратор работает так, как описано выше. Если 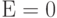 , то на всех выходах дешифратора будут логические 0 независимо от состояния входных сигналов, т.е. все выходы дешифратора будут в пассивном (в рассматриваемом случае нулевом) состоянии.
, то на всех выходах дешифратора будут логические 0 независимо от состояния входных сигналов, т.е. все выходы дешифратора будут в пассивном (в рассматриваемом случае нулевом) состоянии.
Все рассмотренные ранее логические элементы могут быть реализованы в виде отдельных интегральных микросхем (ИМС) малой степени интеграции. Так, сборка из четырёх 2-входовых элементов И-НЕ объединяется в одном корпусе ИС К155ЛА3 [4].
Интегральная микросхема (ИМС) - микроэлектронное изделие, выполняющее определенную функцию преобразования и обработки сигнала и имеющее высокую плотность упаковки электрически соединённых элементов, которое рассматривается как единое целое [4, с.9].
Степень интеграции ИМС - показатель степени сложности микросхемы, характеризующийся числом содержащихся в ней элементов и компонентов [4, с.10]:
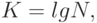
где  - число входящих в ИМС элементов и компонентов.
- число входящих в ИМС элементов и компонентов.
Различают интегральные микросхемы малой ( МИС - малые интегральные схемы), средней ( СИС ), большой ( БИС ) и сверхбольшой ( СБИС ) степени интеграции.
увеличить изображение
Рис. 4.2. Функциональная схема трех-входового дешифратора с разрешающим сигналом
На рис. 4.3 показаны примеры условного графического обозначения (УГО) дешифраторов с активным единичным уровнем входных и выходных сигналов. Здесь и далее на УГО выделяется три поля. Центральное поле содержит обозначение функции, выполняемой ИМС. В данном случае это DC - от англ. D e c oder - дешифратор. Левое поле содержит обозначение входов ИМС, правое - обозначение выходов.
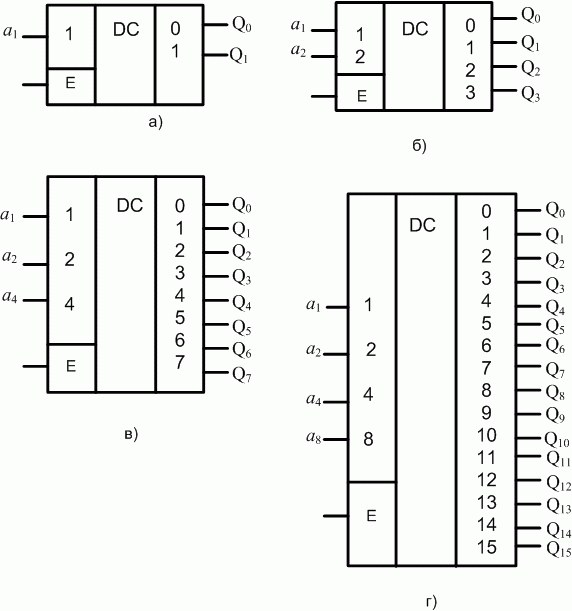
Рис. 4.3. УГО дешифраторов с активными единичными входными и выходными сигналами: а - на один вход; б - на два входа; в - на три входа; г - на четыре входа.
При принятии отрицательной логики, когда активным уровнем всех сигналов является логический ноль, таблица истинности дешифратора на три входа (табл. 4.2) будет содержать в диагонали не единицы, а нули. При этом порядок следования комбинаций входных сигналов в данном случае удобно сделать обратным - в первой строке указать комбинацию  , далее
, далее 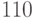 и т.д. до последней строки с комбинацией
и т.д. до последней строки с комбинацией  .
.
| Входные сигналы | Выходные сигналы | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
 |
 |
 |
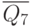 |
 |
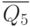 |
 |
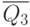 |
 |
 |
 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Активный нулевой уровень сигнала принято обозначать на УГО в виде инверсных входов и выходов так, как представлено на рис. 4.4. Поскольку в каждом столбце табл. 4.2 присутствует один ноль и семь единиц, логическое выражение удобнее представить в виде соответствующих макстермов:
 |
( 4.2) |