Логические основы ЭВМ
Логические схемы
Составление таблиц истинности для логических схем
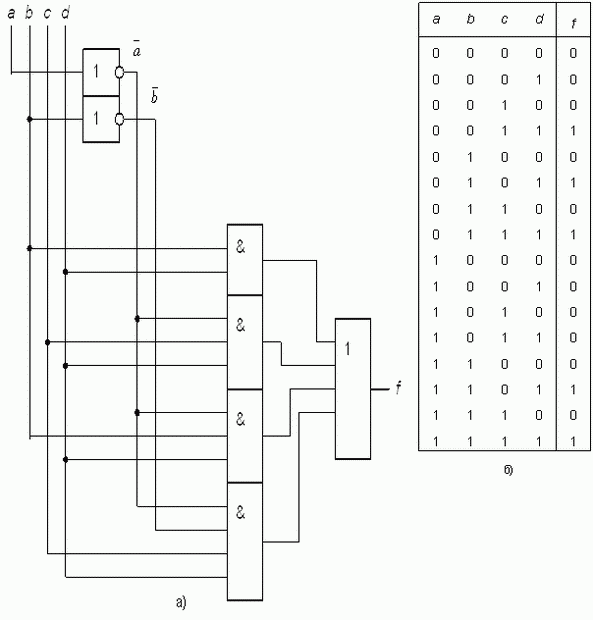
Для логических схем, представляющих собой соединение нескольких логических элементов, в левой части таблицы перечисляются все возможные комбинации входных сигналов, а в правой части - соответствующие значения на выходе логической схемы. Очевидно, что левые части таблицы будут одинаковыми для всех функций двух переменных, для всех функций трёх переменных и т.д. Традиционно комбинации сигналов в них располагают в порядке возрастания соответствующих двоичных кодов. На рис. 1.6 приведен пример логической схемы и таблица истинности, полностью описывающая ее работу.
Вероятность ошибки уменьшается, если не решать задачу "в лоб", а проанализировать её работу с точки зрения уже известных нам правил логического сложения, умножения и инверсии. Очевидно, что в рассматриваемой схеме осуществляется логическое сложение нескольких логических произведений [3]. Можно записать логическое выражение, соответствующее данной схеме:
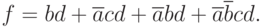 |
( 1.1) |
Булево выражение в виде суммы произведений называется дизъюнктивно нормальной формой (ДНФ).
Булево выражение в виде произведения сумм называется конъюнктивной нормальной формой (КНФ).
По правилу логического сложения выражение (1.1) имеет на выходе логическую 1  только в том случае, если равно 1 хотя бы одно из четырех произведений, входящих в сумму. По правилу логического умножения каждое произведение будет равно 1 только в том случае, когда все входящие в произведение переменные равны 1. Рассмотрим все эти возможности отдельно и по порядку.
только в том случае, если равно 1 хотя бы одно из четырех произведений, входящих в сумму. По правилу логического умножения каждое произведение будет равно 1 только в том случае, когда все входящие в произведение переменные равны 1. Рассмотрим все эти возможности отдельно и по порядку.
- Произведение
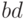 будет равно 1 только тогда, когда будет выполняться условие: и
будет равно 1 только тогда, когда будет выполняться условие: и  , и
, и  . При этом от значений остальных входных переменных -
. При этом от значений остальных входных переменных -  и
и  - значение данного произведения не зависит. Поэтому логические 1 будут в строках, соответствующих полным произведениям
- значение данного произведения не зависит. Поэтому логические 1 будут в строках, соответствующих полным произведениям  , в которых
, в которых 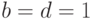 , а переменные
, а переменные  и
и  перечисляются во всех четырех возможных комбинациях:
перечисляются во всех четырех возможных комбинациях:  ,
,  ,
, 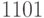 и
и  .
. - Произведение
 будет равно 1 только тогда, когда будет выполняться условие: и
будет равно 1 только тогда, когда будет выполняться условие: и 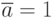 (т.е.
(т.е. 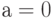 ), и
), и  , и
, и  . От значения не вошедшей в данное произведение переменной
. От значения не вошедшей в данное произведение переменной  произведение
произведение  не зависит. Поэтому логические 1 будут в строках таблицы истинности, соответствующих полным произведениям
не зависит. Поэтому логические 1 будут в строках таблицы истинности, соответствующих полным произведениям  , в которых
, в которых  и одновременно
и одновременно 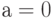 , а переменная
, а переменная  перечисляется во всех двух возможных комбинациях:
перечисляется во всех двух возможных комбинациях:  .
. - Произведение
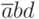 будет равно 1 только тогда, когда будет выполняться условие: и
будет равно 1 только тогда, когда будет выполняться условие: и 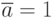 (т.е.
(т.е. 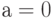 ), и
), и  , и
, и  . От значения не вошедшей в данное произведение переменной
. От значения не вошедшей в данное произведение переменной  произведение
произведение 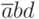 не зависит. Поэтому логические 1 будут в строках таблицы истинности, соответствующих полным произведениям
не зависит. Поэтому логические 1 будут в строках таблицы истинности, соответствующих полным произведениям  , в которых
, в которых 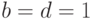 и одновременно
и одновременно 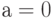 , а переменная
, а переменная  перечисляется во всех двух возможных комбинациях:
перечисляется во всех двух возможных комбинациях: 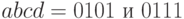 .
. - Произведение
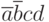 будет равно 1 только тогда, когда будет выполняться условие: и
будет равно 1 только тогда, когда будет выполняться условие: и 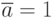 (т.е.
(т.е. 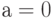 ),
),  (т.е.
(т.е. 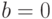 ), и
), и  и
и  . Поэтому логическая 1, соответствующая данному полному произведению всех переменных, будет только в той строке таблицы истинности, где
. Поэтому логическая 1, соответствующая данному полному произведению всех переменных, будет только в той строке таблицы истинности, где  .
.
Анализ всех этих возможностей показывает, что они могут совпадать для нескольких произведений. Например, комбинация входных переменных 0011 встречается в произведениях  и
и 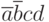 . А сочетание
. А сочетание  встречается даже в трех произведениях: и в
встречается даже в трех произведениях: и в 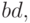 и в
и в  , и в
, и в 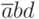 . Это говорит о том, что для данного логического выражения есть возможности минимизации.Правила минимизации рассматриваются в лекции 2.
. Это говорит о том, что для данного логического выражения есть возможности минимизации.Правила минимизации рассматриваются в лекции 2.
Ключевые термины
ДНФ - дизъюнктивно-нормальная форма - представление логического выражения в виде суммы произведений.
Инверсия - операция НЕ- логическое действие, при котором появление хотя бы одного логического нуля на входе даёт логическую единицу на выходе.
Инвертор - логический элемент, реализующий операцию НЕ.
КНФ - конъюктивно-нормальная форма - представление логического выражения в виде произведения сумм.
Логическая переменная - переменная, значение которой может быть равно либо логическому нулю, либо логической единице.
Логическая схема - схема, состоящая из логических элементов.
Логическая функция - функция, включающая в себя логические переменные, значение которой может быть равно либо логическому нулю, либо логической единице.
Логический элемент - графическое представление элементарной логической функции.
Логическое отрицание - операция НЕ, инверсия - логическое действие, при котором происходит изменение состояния на противоположное.
Логическое сложение - операция ИЛИ, дизъюнкция - логическое действие, при котором появление хотя бы одной логической единицы на входе даёт логическую единицу на выходе.
Логическое умножение - операция И, конъюнкция - логическое действие, при котором появление хотя бы одного логического нуля на входе даёт логический нуль на выходе.
Таблица истинности - таблица, содержащая все возможные комбинации входных логических переменных и соответствующие им значения логической функции.
Краткие итоги
Любая цифровая вычислительная машина состоит из логических схем. Логические схемы, в свою очередь, состоят из логических элементов. Самыми простыми логическими элементами являются элементы И, ИЛИ и НЕ. Им соответствуют функции логического умножения, сложения и инверсии.
Набор для практики
Вопросы для самопроверки
- Нарисуйте элементы И на два, четыре и пять входов, составьте для каждого из них таблицу истинности, напишите соответствующее каждому элементу логическое выражение.
- Нарисуйте элементы ИЛИ на три, четыре и пять входов, составьте для каждого из них таблицу истинности, напишите соответствующее каждому элементу логическое выражение.
- Нарисуйте элементы И-НЕ на два, четыре и пять входов, составьте для каждого из них таблицу истинности, напишите соответствующее каждому элементу логическое выражение.
- Нарисуйте элементы ИЛИ-НЕ на три, четыре и пять входов, составьте для каждого из них таблицу истинности, напишите соответствующее каждому элементу логическое выражение.
- Какой уровень сигнала является решающим для логического сложения? для логического умножения? для функции И-НЕ? для функции ИЛИ-НЕ?
- Что такое таблица истинности?
- Сколько строк в таблице истинности для 5-входовой логической схемы? для 4-входовой? для 2-входовой?
- Функция скольких переменных описывается таблицей истинности длиной 4 строки? 64 строки? 512 строк?