|
Хотелось бы иметь возможность читать текст сносок при использовании режима "Версия для печати" |
Проектирование реляционных баз данных на основе принципов нормализации: дальнейшая нормализация
Зависимости проекции/соединения и пятая нормальная форма
Приведение отношения к 4NF предполагает его декомпозицию без потерь на две проекции (как и в случае 2NF, 3NF и BCNF). Однако бывают (хотя и нечасто) случаи, когда декомпозиция без потерь на две проекции невозможна, но можно произвести декомпозицию без потерь на большее число проекций. Будем называть n-декомпозируемым отношением отношение, которое может быть декомпозировано без потерь на n проекций. До сих пор мы имели дело с 2-декомпозируемыми отношениями.
N-декомпозируемые отношения
Начнем с еще одного определения.
В переменной отношения r с атрибутами (возможно, составными) A и B MVD A->->B называется тривиальной, если либо 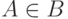 , либо A UNION B совпадает с заголовком отношения r .
, либо A UNION B совпадает с заголовком отношения r .
Тривиальная MVD всегда удовлетворяется. При 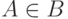 она вырождается в тривиальную FD. В случае A UNION B = Hr требования многозначной зависимости соблюдаются очевидным образом.
она вырождается в тривиальную FD. В случае A UNION B = Hr требования многозначной зависимости соблюдаются очевидным образом.
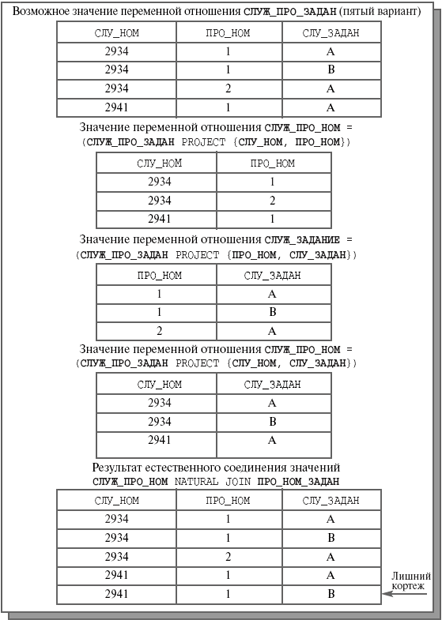
Для примера n-декомпозируемого отношения при n > 2 рассмотрим пятый вариант переменной отношения СЛУЖ_ПРО_ЗАДАН, в которой имеется единственно возможный ключ {СЛУ_НОМ, ПРО_НОМ, СЛУ_ЗАДАН} и отсутствуют нетривиальные MVD. Пример значения переменной отношения приведен на рис. 8.3.
Как показано на рис. 8.3, результат естественного соединения проекций СЛУЖ_ПРО_НОМ и ПРО_НОМ_ЗАДАН почти совпадает с телом исходного отношения СЛУЖ_ПРО_ЗАДАН, но в нем присутствует один лишний кортеж, который исчезнет после выполнения заключительного естественного соединения с проекцией СЛУЖ_ЗАДАНИЕ. Читателям предлагается убедиться, что исходное отношение будет восстановлено при любом порядке естественного соединения трех проекций.
Зависимость проекции/соединения
Утверждение о том, что тело отношения СЛУЖ_ПРО_ЗАДАН восстанавливается без потерь путем естественного соединения его проекций СЛУЖ_ПРО_НОМ, ПРО_НОМ_ЗАДАН и СЛУЖ_ЗАДАНИЕ эквивалентно следующему утверждению ( ТСПЗ, ТСПН, ТПНЗ и ТСЗ обозначают тела значений переменных отношений СЛУЖ_ПРО_ЗАДАН, СЛУЖ_ПРО_НОМ, ПРО_НОМ_ЗАДАН и СЛУЖ_ЗАДАНИЕ соответственно):
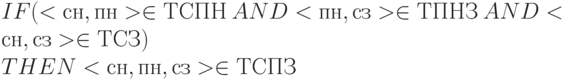
Чтобы возможность восстановления без потерь отношения СЛУЖ_ПРО_ЗАДАН путем естественного соединения его проекций СЛУЖ_ПРО_НОМ, ПРО_НОМ_ЗАДАН и СЛУЖ_ЗАДАНИЕ существовала при любом допустимом значении переменной отношения СЛУЖ_ПРО_ЗАДАН, должно поддерживаться следующее ограничение:
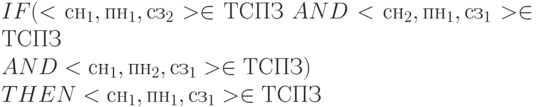
Это обычное ограничение реального мира, которое для отношения СЛУЖ_ПРО_ЗАДАН может быть сформулировано на естественном языке следующим образом:
Если служащий с номером сн участвует в проекте пн, и в проекте пн выполняется задание сз, и служащий с номером сн выполняет задание сз, то служащий с номером сн выполняет задание сз в проекте пн.
В общем виде такое ограничение называется зависимостью проекции/соединения. Вот формальное определение.
Пусть задана переменная отношения r, и A, B, …, Z являются произвольными подмножествами заголовка r (составными, перекрывающимися атрибутами). В переменной отношения r удовлетворяется зависимость проекции/соединения (Project-Join Dependency – PJD) *( A, B, …, Z) тогда и только тогда, когда любое допустимое значение r можно получить путем естественного соединения проекций этого значения на атрибуты A, B, …, Z .