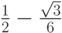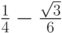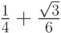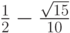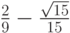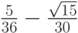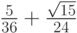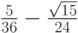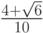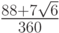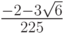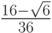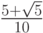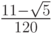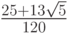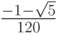НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 10: Численные методы решения жестких систем обыкновенных дифференциальных уравнений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Уровень: специалист | Доступ: свободно | ВУЗ: Московский физико-технический институт

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать программу

9.4. Численные методы решения ЖС ОДУ. Семейства неявных методов Рунге - Кутты и Розенброка

Рассмотрим другие методы для численного решения как линейных жестких систем ОДУ вида (9.1), так и нелинейных систем общего вида

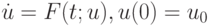
$\dot {u} = {F}(t;{u}), {u}(0) = u_0$

и автономных ЖС ОДУ

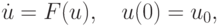
$\dot {u} = {F}(u), \quad {u}(0) = u_0,$

см. также [9.1], [9.4], [9.9], [9.13], [9.14], [9.15], [9.16]. Из соображений устойчивости метода предпочтение естественно отдать неявным методам. Простейшими из них являются:

неявный метод Эйлера (приведем его вид для случая автономной ЖС ОДУ, для неавтономной системы формулы очевидны):
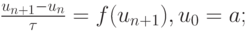
$\frac{u_{n + 1} - u_n}{{\tau}} = f(u_{n + 1}), u_0 = a;$
метод трапеций
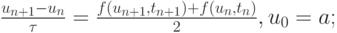
$$ \frac{u_{n + 1} - u_n}{{\tau}} = \frac{f(u_{n + 1}, t_{n + 1}) + f(u_n, t_n)}{2}, u_0 = a;$
метод прямоугольников (правило средней точки)
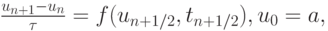
$\frac{u_{n + 1} - u_n}{{\tau}} = f(u_{n + 1/2}, t_{n + 1/2}), u_0 = a,$

где

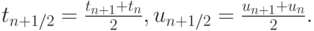
$t_{n + 1/2} = \frac{t_{n + 1} + t_n}{2}, u_{n + 1/2} = \frac{u_{n + 1} + u_n}{2}.$

Среди одношаговых методов для решения жестких систем наиболее известны методы Рунге-Кутты. Все приведенные в данном параграфе формулы можно рассматривать как частные случаи неявных одно - и двухстадийных методов из этого семейства. Не останавливаясь на получении приводимых коэффициентов, выпишем наиболее известные из формул Рунге - Кутты, используя таблицу Бутчера. О представлении методов Рунге - Кутты в виде таблиц Бутчера — в "Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений" .

Отметим, что в отличие от рассматриваемых выше явных методов, при использовании неявных схем Рунге - Кутты матрица коэффициентов метода в таблице Бутчера — заполненная, и для определения вспомогательных векторов, входящих в функцию приращения, приходится решать систему нелинейных алгебраических уравнений.

Методы Гаусса соответственно 2 - го, 4 - го, и 6 - го порядков представлены в табл. 9.1, 9.2, 9.3. Основаны эти методы на соответствующих квадратурных формулах Гаусса, рассмотренных в "Численное интегрирование" . Первый метод совпадает с правилом средней точки. Второй метод (4 - го порядка) носит название метода Хаммера - Холлинсворта.

Таблица 9.1.
1/2 1/2

1

Таблица 9.2.

$\frac{1}{2} - \frac{\sqrt{3}}{6}$

$\frac{1}{4}$

$\frac{1}{4} - \frac{\sqrt{3}}{6}$

$\frac{1}{2} + \frac{\sqrt{3}}{6}$

$\frac{1}{4} + \frac{\sqrt{3}}{6}$

$\frac{1}{4}$

1/2 1/2

Таблица 9.3.

$\frac{1}{2} - \frac{\sqrt{15}}{10}$

$\frac{5}{36}$

$\frac{2}{9} - \frac{\sqrt{15}}{15}$

$\frac{5}{36} - \frac{\sqrt{15}}{30}$

$\frac{1}{2}$

$\frac{5}{36} + \frac{\sqrt{15}}{24}$

$\frac{2}{9}$

$\frac{5}{36} - \frac{\sqrt{15}}{24}$

$\frac{1}{2} + \frac{\sqrt{15}}{10}$

$\frac{5}{36} + \frac{\sqrt{15}}{30}$

$\frac{2}{9} + \frac{\sqrt{15}}{15}$

$\frac{5}{36}$

$\frac{5}{18}$

$\frac{4}{9}$

$\frac{5}{18}$
Методы Радо IIA порядков 1, 3, 5 представлены соответственно в табл. 9.4, 9.5, 9.6. Основаны на квадратурных формулах Радо, принадлежащих к семейству формул Гаусса. Метод первого порядка является неявным методом Эйлера.

Таблица 9.4.
1 1

1

Таблица 9.5.
1/3 5/12 - 1/12

1 3/4 1/4

3/4 1/4

Таблица 9.6.

$\frac{4 - \sqrt{6}}{10}$
$88 - 7\sqrt{6} $$
$\frac{296 - 169\sqrt{6}}{1 800}$

$\frac{- 2 + 3\sqrt{6}}{225}$

$\frac{4 + \sqrt{6}}{10}$

$\frac{296 + 169\sqrt{6}}{1 800}$

$\frac{88 + 7\sqrt{6}}{360}$

$\frac{- 2 - 3\sqrt{6}}{225}$

1
$\frac{16 - \sqrt{6}}{36}$

$\frac{16 + \sqrt{6}}{36}$

$\frac{1}{9}$

$\frac{16 - \sqrt{6}}{36}$

$\frac{16 + \sqrt{6}}{36}$

$\frac{1}{9}$
Методы Лобатто IIIА 2-го, 4-го и 6-го порядков точности см. в табл. 9.7, 9.8, 9.9 и 9.10 соответственно. Видно, что метод второго порядка точности является неявным методом трапеций.

Таблица 9.7.
0 0 0

1 1/2 1/2

1/2 1/2

Таблица 9.8.
0 0 0 0

1/2 5/24 1/3 - 1/24

1 1/6 2/3 1/6

1/6 2/3 1/6

Таблица 9.9.
0 0 0 0 0

$\frac {5 - \sqrt{5}}{10}$
$\frac{11 + \sqrt{5}}{120}$

$\frac{25 - \sqrt{5}}{120}$

$\frac{25 - 13\sqrt{5}}{120}$

$\frac{- 1 + \sqrt{5}}{120}$

$\frac {5 + \sqrt{5}}{10}$
$\frac{11 - \sqrt{5}}{120}$

$\frac{25 + 13\sqrt{5}}{120}$

$\frac{25 + \sqrt{5}}{120}$

$\frac{- 1 - \sqrt{5}}{120}$

1 1/12 5/12 5/12 1/12

1/12 5/12 5/12 1/12

Рассмотрим теперь, как строится функция устойчивости для методов Рунге - Кутты [9.4]. Уже отмечалось выше, что при построении функции устойчивости рассматривается модельное уравнение вида

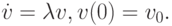
$\dot {v} = \lambda v, v(0) = v_0.$
Запишем теперь метод Рунге - Кутты для решения приведенного выше уравнения в общей форме с использованием новых переменных Y:

$\begin{gather*} v_{{n} + 1} = v_n + {\tau}\sum {\gamma_p f(t_n + \alpha_p {\tau}, Y_p) \equiv v_n + {\tau}\lambda \sum {\gamma_p Y_p} }, \\ Y_p = v_n + {\tau}\sum\limits_{k = 1}^{s}{\beta_{{kp}} f(t_n + \gamma_k {\tau}, Y_k) \equiv v_n + {\tau}\lambda \sum {\beta_{{kp}} Y_k} }. \end{gather*}$

Приведенные выше формулы можно рассматривать как систему линейных уравнений относительно новых переменных Y₁, ..., Y_k, v_{n + 1} следующего вида:

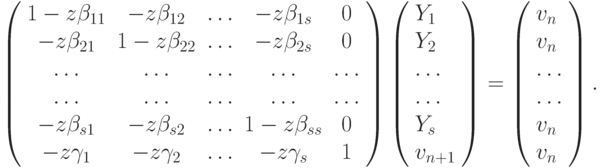
$\left( \begin{array}{ccccc} {1 - z\beta_{11}} & {- z\beta_{12}} & \ldots & {- z\beta_{1s}} & 0 \\ {- z\beta_{21}} & {1 - z\beta_{22}} & \ldots & {- z\beta_{2s}} & 0 \\ \ldots & \ldots & \ldots & \ldots & \ldots \\ \ldots & \ldots & \ldots & \ldots & \ldots \\ {- z\beta_{s1}} & {- z\beta_{s2}} & \ldots & {1 - z\beta_{ss}} & 0 \\ {- z\gamma_1 } & {- z\gamma_2 } & \ldots & {- z\gamma_{s}} & 1 \\ \end{array} \right) \left( \begin{array}{l} {Y_1 } \\ {Y_2 } \\ \ldots \\ \ldots \\ {Y_s} \\ {v_{n + 1}} \\ \end{array} \right) = \left( \begin{array}{l} {v_n} \\ {v_n} \\ \ldots \\ \ldots \\ {v_n} \\ {v_n} \\ \end{array} \right) .$

Необходимо выразить v_{n + 1} через v_n. Для этого воспользуемся правилом Крамера. Ответ можно записать в следующей форме:

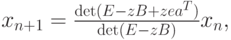
$x_{n + 1} = \frac{\det (E - zB + zea^T)}{\det (E - zB)}x_n,$

где E — единичная матрица размера S x S, B - матрица коэффициентов 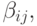$\beta_{ij},$ входящая в таблицу Бутчера, E — единичный вектор размерности S (столбец), a^T — строка коэффициентов $\gamma _{1},$ входящая в таблицу Бутчера, S — число стадий метода Рунге - Кутты.

Условием устойчивости метода будет

$\left|{\frac{\det (E - z B + z ea^T)}{\det (E - zB)}}\right| < 1.$

Таблица 9.1.
1/2	1/2
	1

Таблица 9.2.
$\frac{1}{2} - \frac{\sqrt{3}}{6}$	$\frac{1}{4}$	$\frac{1}{4} - \frac{\sqrt{3}}{6}$
$\frac{1}{2} + \frac{\sqrt{3}}{6}$	$\frac{1}{4} + \frac{\sqrt{3}}{6}$	$\frac{1}{4}$
	1/2	1/2

Таблица 9.3.
$\frac{1}{2} - \frac{\sqrt{15}}{10}$	$\frac{5}{36}$	$\frac{2}{9} - \frac{\sqrt{15}}{15}$	$\frac{5}{36} - \frac{\sqrt{15}}{30}$
$\frac{1}{2}$	$\frac{5}{36} + \frac{\sqrt{15}}{24}$	$\frac{2}{9}$	$\frac{5}{36} - \frac{\sqrt{15}}{24}$
$\frac{1}{2} + \frac{\sqrt{15}}{10}$	$\frac{5}{36} + \frac{\sqrt{15}}{30}$	$\frac{2}{9} + \frac{\sqrt{15}}{15}$	$\frac{5}{36}$
	$\frac{5}{18}$	$\frac{4}{9}$	$\frac{5}{18}$

Таблица 9.4.
1	1
	1

Таблица 9.5.
1/3	5/12	- 1/12
1	3/4	1/4
	3/4	1/4

Таблица 9.6.
$\frac{4 - \sqrt{6}}{10}$	$88 - 7\sqrt{6} $$	$\frac{296 - 169\sqrt{6}}{1 800}$	$\frac{- 2 + 3\sqrt{6}}{225}$
$\frac{4 + \sqrt{6}}{10}$	$\frac{296 + 169\sqrt{6}}{1 800}$	$\frac{88 + 7\sqrt{6}}{360}$	$\frac{- 2 - 3\sqrt{6}}{225}$
1	$\frac{16 - \sqrt{6}}{36}$	$\frac{16 + \sqrt{6}}{36}$	$\frac{1}{9}$
	$\frac{16 - \sqrt{6}}{36}$	$\frac{16 + \sqrt{6}}{36}$	$\frac{1}{9}$

Таблица 9.7.
0	0	0
1	1/2	1/2
	1/2	1/2

Таблица 9.8.
0	0	0	0
1/2	5/24	1/3	- 1/24
1	1/6	2/3	1/6
	1/6	2/3	1/6

Таблица 9.9.
0	0	0	0	0
$\frac {5 - \sqrt{5}}{10}$	$\frac{11 + \sqrt{5}}{120}$	$\frac{25 - \sqrt{5}}{120}$	$\frac{25 - 13\sqrt{5}}{120}$	$\frac{- 1 + \sqrt{5}}{120}$
$\frac {5 + \sqrt{5}}{10}$	$\frac{11 - \sqrt{5}}{120}$	$\frac{25 + 13\sqrt{5}}{120}$	$\frac{25 + \sqrt{5}}{120}$	$\frac{- 1 - \sqrt{5}}{120}$
1	1/12	5/12	5/12	1/12
	1/12	5/12	5/12	1/12

Одноитерационные методы Розенброка. Розенброком был предложен класс неявных методов, в котором не решается система нелинейных уравнений. В простейшем случае для автономной системы уравнений методы типа Розенброка могут иметь вид [9.3]

$(E - a {\tau}B - b {\tau}^2 B^2 ) \frac{u_{n + 1} - u_n}{{\tau}} = f[u_n + c{\tau}f(u_n)] .$

Здесь

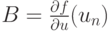
$B = \frac{\partial f}{\partial u}(u_n)$

матрица, постоянная на данном шаге по времени. Параметры a, b, c подбираются таким образом, чтобы обеспечить максимально возможный порядок точности.

Например, для схемы третьего порядка точности получим

a = 1, 077;   b = - 0, 372;   c = - 0, 577 .

Такую схему иногда называют методом с одной итерацией, имея в виду, что вычисление обратной матрицы сравнимо по количеству арифметических операций с одной итерацией метода Ньютона. Преимущество методов типа Розенброка перед прочими классами численных методов ЖС ОДУ заключается в том, что для определения решения на верхнем временном слое необходимо решать уже линейную систему алгебраических уравнений.

Рассмотрим связь между методами Розенброка и Рунге - Кутты.

Определение. ([9.9]) S - стадийный метод Розенброка для решения автономной системы ЖС ОДУ имеет вид

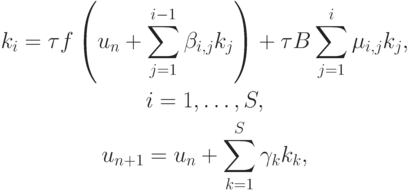
$\begin{gather*} k_i = {\tau}f \left({u_n + \sum\limits_{j = 1}^{i - 1}{\beta_{i, j}k_j}}\right) + {\tau}B \sum\limits_{j = 1}^{i}{\mu_{i, j}k_j}, \\ i = 1, \ldots , S, \\ u_{n + 1} = u_n + \sum\limits_{k = 1}^{S}{\gamma_k k_k}, \end{gather*}$

где 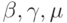$\beta, \gamma, \mu$ — управляющие коэффициенты метода. Как и выше, матрица Якоби правой части системы B вычисляется по данным в точке t_n. Связь последних формул с выражениями для явных методов Рунге - Кутты очевидна.

Несколько сложнее представляются методы Розенброка в случае неавтономной ЖС ОДУ [9.9]:

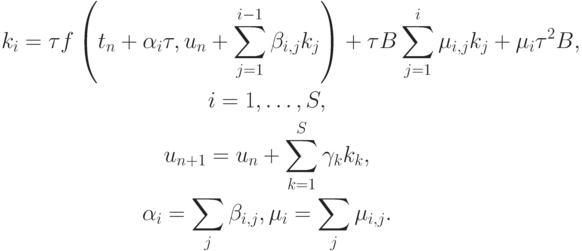
$\begin{gather*} k_i = {\tau}f \left({t_n + \alpha_i {\tau}, u_n + \sum\limits_{j = 1}^{i - 1}{\beta_{i, j}k_j} }\right) + {\tau}B\sum\limits_{j = 1}^{i}{\mu_{i, j}k_j} + \mu_i \tau^2 B, \\ i = 1, \ldots , S, \\ u_{n + 1} = u_n + \sum\limits_{k = 1}^{S}{\gamma_k k_k}, \\ \alpha_i = \sum\limits_j \beta_{i, j}, \mu_i = \sum\limits_j{\mu_{i, j}}. \end{gather*}$

Вывод условий порядка методов Розенброка — достаточно громоздкий, и всем заинтересованным читателям можно рекомендовать разобраться в выкладках в книге [9.9]. Отметим, что широкое распространение получают в последнее время вложенные методы Розенброка высокого порядка аппроксимации, имеющие очень хорошие вычислительные качества. Возможно, что новые методы типа Розенброка способны будут вытеснить из вычислительной практики наиболее распространенные до этого в вычислительной практике методы Гира.

Дальше >>

Авторизоваться

Введение в вычислительную математику

Лекция 10: Численные методы решения жестких систем обыкновенных дифференциальных уравнений

9.4. Численные методы решения ЖС ОДУ. Семейства неявных методов Рунге - Кутты и Розенброка

Вопросы и ответы