Распараллеливание в ВС на уровне исполнительных устройств
Конвейеры операций
Выполнение любой операции складывается из нескольких последовательных этапов, каждый из которых может выполняться своим функциональным узлом. Это легко показать на операциях сложения и умножения. Выполнение деления мантисс (порядки вычитаются) чаще всего производятся с помощью вычитания из делимого делителя, сдвига влево полученного остатка, нового вычитания делителя из результата сдвига и т.д. В некоторых ВС находится обратная величина делителя с помощью аппроксимирующих полиномов. Затем делимое умножается на эту величину.
Пусть задана операция, выполнение которой разбито на n последовательных этапов. Пусть ti — время выполнения i -го этапа. При последовательном их выполнении операция выполняется за время
![t_\text{посл}=\sum_{i=1}^{n} t_{i}[c]
,](/sites/default/files/tex_cache/1446166de8c789a01d409e5ee107bc3f.png)
![S_\text{посл} = \frac{1}{t_\text{посл}} = \frac{1}{\sum_{i=1}^{n}t_i} [\text{операций/с}]
.](/sites/default/files/tex_cache/a2c3706669cfb0f8ef623a2505b62a8e.png)
Функциональные узлы, выполняющие последовательные этапы одной операции, целесообразно выстроить в единую конвейерную линию, где устройство, выполняющее некоторый этап, закончив его для операции над одним набором данных, переходило бы в следующем такте к выполнению этого же этапа той же операции для другого набора исходных данных.
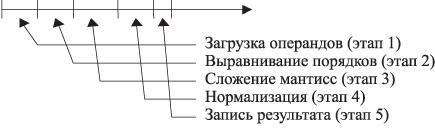
Например, на рис. 3.1 представлен конвейер выполнения операции сложения.
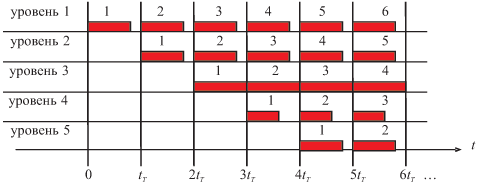
Пусть реализуется поток команд одного процессора или существует доступ к этому устройству нескольких процессоров так, что в каждом такте возможно задание на выполнение сложения новой пары чисел. Тогда временная диаграмма работы конвейера может иметь вид, представленный на рис. 3.2.
Максимальное быстродействие процессора при полной загрузке конвейера составляет
![S_{\text{кон}} =\frac{1}{t_{T}}[\text{операций}/c].](/sites/default/files/tex_cache/8e13ffc0347c1473f3b98bc46d73214f.png)
Число n — количество уровней конвейера, или глубина перекрытия, т.к. каждый такт на конвейере параллельно выполняются n операций. Чем больше число уровней (станций), тем больший выигрыш в быстродействии может быть получен.
В проекте МВК "Эльбрус-3" АЛУ его ЦП имеет конвейерные ИУ сложения ( n=5 ), умножения ( n=5 ), деления ( n=8 для полусловного формата, — 32 разряда, n=16 для словного формата). Логические операции также выполняются на конвейере с n=2.
Известна оценка
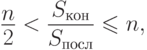
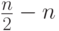 раз.
раз.Реальный выигрыш в быстродействии оказывается всегда меньше, чем указанный выше, поскольку:
- некоторые операции, например, над целыми, могут выполняться за меньшее количество этапов, чем другие арифметические операции. Тогда отдельные станции конвейера будут простаивать.
- при выполнении некоторых операций на определённых этапах могут требоваться результаты более поздних, ещё не выполненных этапов предыдущих операций. Приходится приостанавливать конвейер.
- поток команд порождает недостаточное количество операций для полной загрузки конвейера.
Векторные конвейеры. "Зацепление" векторов
Наряду с использованием конвейеров для обработки единичных (скалярных) данных, используют так называемые векторные конвейеры, единичной информацией для которых являются вектора — массивы данных. Применение векторных конвейеров определило класс ВС — векторно-конвейерных ВС, сегодня ещё являющихся основой построения некоторых супер-ЭВМ — ВС сверхвысокой производительности.
Для эффективности векторно-конвейерных ВС (например, для подготовки алгоритмов решения задач на ВС "Электроника-ССБИС") необходима векторизация задач. Это — такое преобразование алгоритма, при котором максимально выделяются (если не вся задача сводится к этому) элементы обработки массивов данных одинаковыми операциями. Сюда входят все задачи, основанные на матричных преобразованиях, обработка изображений, сигналов, моделирование поведения среды и т.д.
В основе векторного конвейера лежит то же самое разбиение операции на уровни или этапы выполнения, но он дополняется средствами аппаратной поддержки, позволяющими по информации о векторах организовать последовательную загрузку конвейера элементами векторов, учитывая их длину.
Пусть необходимо выполнить операцию C = A x B,
т.е. cj = aj + bj, j = 1, ...,N.
Пусть на регистрах СОЗУ записаны вектора A и B.
Группа регистров отведена для результатов C. Для управления
этим процессом известны дескрипторы векторов DA ,DB ,DC, где 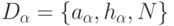 ,
, 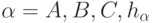 — шаг
переадресации. Если загрузка векторов производится всегда в одни и те же
регистры АЛУ, то достаточно знать значение N. Может задаваться
маска M длиной N, состоящая из нулей и единиц. Каждый
элемент M соответствует элементу вектора-результата C. Если элемент mj = 1 (логическая переменная), то операция
получения cj производится, в противном случае соответствующие
элементы векторов пропускаются. Это применимо для альтернативного счёта в
соответствии со значением логических переменных.
— шаг
переадресации. Если загрузка векторов производится всегда в одни и те же
регистры АЛУ, то достаточно знать значение N. Может задаваться
маска M длиной N, состоящая из нулей и единиц. Каждый
элемент M соответствует элементу вектора-результата C. Если элемент mj = 1 (логическая переменная), то операция
получения cj производится, в противном случае соответствующие
элементы векторов пропускаются. Это применимо для альтернативного счёта в
соответствии со значением логических переменных.
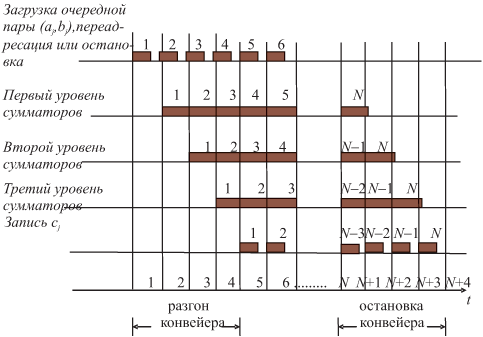
Пусть операция умножения выполняется за три этапа. Тогда можно представить временную диаграмму получения N результатов при предположении о назначении функциональных устройств (рис. 3.3).
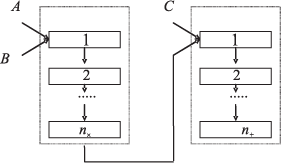
В составе АЛУ может быть два и более конвейерных устройств, специализированных каждое для выполнения некоторой операции. Тогда возможно и эффективно "зацепление" векторов, иллюстрируемое примером на рис. 3.4 для выполнения сложной операции над векторами: D=Ax B+C.
Здесь два конвейера образовали один, с глубиной перекрытия n = nx + n+. Очередной результат умножения немедленно направляется на конвейер сложения, куда параллельно направляется необходимый сомножитель.