Общие сведения о функциях языка С
Пример 3. Напишите программу поиска максимального элемента среди минимальных элементов строк двухмерного целочисленного массива.
Условие примера соответствует поиску максимина в двухмерном массиве, т.е.
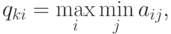
где  – элементы матрицы
– элементы матрицы  .
.
Алгоритм поиска максмина заключается в следующем [10.6]. Сначала предполагаем, что максимальным элементом является начальный элемент первой строки A[0][0], затем заменяем его минимальным элементом этой же строки, т.е. теперь минимальный элемент первой строки принимается за искомый максимум. Последовательно просматривая остальные строки, находим в каждой из них минимальный элемент. Если окажется, что минимальный элемент текущей строки больше текущего максимума, то он принимается за максимальный. Результатом поиска являются значение максимального элемента и его индексы (номер строки и номер столбца).
Программный код решения примера:
#include <stdio.h>
#include <conio.h>
#include <stdlib.h>
#include <time.h>
#define n 6
#define m 7
const int N = 100;
int main (void)
{
//Прототип функции
int MaxMin(int A[][m], int nn, int mm, int *imax, int *jmax);
int i, j, A[n][m], max, imax, jmax;
long int L;
L = (long) time(NULL);
srand((unsigned)L);
//Заполнение матрицы целыми случайными числами
for (i = 0; i < n; ++i)
for (j = 0; j < m; ++j)
A[i][j] = 2*N*rand()/RAND_MAX - N;
// Распечатка матрицы
printf("\n\t The original matrix A(%d*%d):\n\n", n, m);
for (i = 0; i < n; ++i){
printf("\t");
for (j = 0; j < m; ++j)
printf("%4d", A[i][j]);
printf("\n");
}
max = MaxMin(A, n, m, &imax, &jmax);
printf("\n\t Result: MaxMin = A[%d][%d] = %d\n", imax+1, jmax+1, max);
printf("\n Press any key: ");
_getch();
return 0;
}
// Функция поиска максмина
int MaxMin(int A[][m], int nn, int mm, int *imax, int *jmax)
{
int i, j, min, max, imin, jmin;
max = A[0][0];
*imax = 0; *jmax = 0;
for (j = 1; j < mm; ++j)
if (A[0][j] < max)
{max = A[0][j]; *imax = 0; *jmax = j;}
for (i = 1; i < nn; ++i) {
min = A[i][0]; imin = i; jmin = 0;
for (j = 1; j < mm; ++j)
if (A[i][j] < min)
{min = A[i][j]; imin = i; jmin = j;}
if (max < min)
{max = min; *imax = imin; *jmax = jmin;}
}
return max;
}В программе поиск максмина выполняется на основе обычной индексации двухмерного массива. В объявлении функции MaxMin() для матрицы явно указывается только второй размер – количество столбцов. Указатели *imax, *jmax используются для передачи в вызывающую функцию индексов найденного максимина. Возвращение самого максимина осуществляется по значению с помощью оператора return, т.е. return max. Вывод значений индексов максмина сделан традиционно в соответствии с принятой обычной математической индексацией.
Возможный результат выполнения программы показан на рис. 10.4.
Задание 3
- Подсчитайте число итераций, используемых при поиске максмина.
- В объявлении матрицы MaxMin() (и ее прототипа) примените указатель на одномерный массив, например, int *a вместо int A[ ][m].
- Число строк матрицы задайте как 3*Х, где Х – номер компьютера, за которым выполняется лабораторная работа.
- Размерность анализируемого массива (матрицы) задайте с клавиатуры. С клавиатуры задайте также интервал генерирования случайных чисел функцией rand() в виде [–2*Х; 2*Х], где Х – номер компьютера, за которым выполняется лабораторная работа.
- Напишите функцию определения субмаксмина, т.е. максимального числа среди минимальных чисел строк двухмерного массива после найденного максимина.
- Определите абсолютные значения максимума и минимума сформированной матрицы, для которой находится максимин.
Пример 4. Напишите программу поиска одного элемента в линейной неупорядоченной таблице по совпадению ключа на основе заграждающего элемента. Таблицу опишите в виде одномерного массива целых чисел [10.6].
В линейной таблице элементы располагаются друг за другом, т.е. для каждого элемента таблицы существуют отношения порядка [10.6]. Линейные таблицы в оперативной памяти компьютера отображаются в массивы или линейные связанные списки.
Поиск одного элемента в неупорядоченной таблице по заданному условию осуществляется последовательным просмотром элементов или до нахождения искомого элемента, т.е. до выполнения условия поиска, или до конца таблицы, если искомый элемент не найден. Возвращаемыми значениями являются адрес (индекс) элемента, или значение элемента, либо признак отсутствия элемента [10.6].
В случае применения заграждающего элемента последняя запись таблицы запоминается, а после завершения поиска восстанавливается в таблице. В последний элемент массива (когда таблица представляется в виде одномерного массива данных) заносится ключ поиска, и образуется так называемый заграждающий элемент. Теперь на каждом шаге поиска осуществляется только одно сравнение, а сам поиск продолжается до нахождения элемента с заданным ключом. Если искомого элемента в исходной таблице не было, то поиск закончится на заграждающем элементе. Использование заграждающего элемента в случае числовых ключей существенно сокращает количество сравнений.
Программный код решения примера:
#include <stdio.h>
#include <conio.h>
#define size 10
// Таблица числовых элементов
int A[size] = {1,-7,3,4,8,-5,-2,6,0,9};
int main (void) {
int i, ind, key;
int search(int A[], int n, int key);
printf("\n\t The original array:\n\t");
for (i = 0; i < size; ++i)
printf("%3d", A[i]);
// Поиск ключа соответствия
printf("\n\n\t Search for key matches.\n");
// Ввод ключа поиска
printf("\t Key in your search: ");
scanf_s("%i", &key);;
ind = search(A, size, key);
if (ind == -1)
printf("\n\t Element \"%d\" could not be found\n", key);
else
printf("\n\t Element \"%d\" index is %d\n", key, ind+1);
printf("\n Press any key: ");
_getch();
return 0;
}
int search(int A[], int n, int key) {
int i = 0, r;
r = A[n-1];
A[n-1] = key;// Заграждающий элемент
while (A[i] != key)
i++;
A[n-1] = r; //Восстановление последнего элемента
if ((i == n-1) && (r != key))
return -1; // Отсутствие элемента
elseF
return i; // Успешный поиск
}В программе использовано внешнее объявление одномерного массива с инициализацией. Термин "внешний" здесь используется, чтобы подчеркнуть расположение объявление вне функций; напрямую с ключевым словом extern он не связан [10.4].
Возможный результат выполнения программы показан на рис. 10.5.


