Динамическое распределение памяти в языке С

Задание 1

1. Вывод символьного массива осуществите на основе его разыменования.
2. Вместо функции calloc() примените функцию malloc() и введите (а потом выведите) свои фамилию, имя, номер группы, специальность (буквами латинского алфавита).
3. Количество вводимых строк определите случайным образом из интервала целых чисел [3;7].
4. Видоизмените программу для ввода одной строки с несколькими словами различной длины (с различным количеством символов), а затем сформируйте массив строк из заданных слов. Предусмотрите вывод строк сформированного символьного массива.
5. Отсортируйте символьный массив по убыванию длин введенных слов, считая, что прописные буквы имеют приоритет над строчными буквами. Сделайте вывод отсортированного массива на дисплей.

Пример 2. Напишите программу для представления нижней треугольной матрицы, размер которой задается пользователем с клавиатуры и заполняется случайными равномерно распределенными числами из интервала [0; 12].

Квадратная матрица [ ] называется нижней треугольной, если из условия i < k следует, что , где i – номер строки, k – номер столбца квадратной матрицы размера n.

В случае прямоугольной матрицы размером n 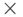m переменные i и k изменяются в пределах: 1 i n, 1 k m.

Программная реализация решения примера основывается на программе из [8].

Программный код решения примера:

#include <stdio.h>
#include <conio.h>
#include <stdlib.h>
#include <time.h>
// Макрос
#define READIn(VARIABLE) \
{printf("\n\t Enter the dimention of a square matrix (not exceeding 12):\n\t ");\
printf(#VARIABLE" = "); scanf_s("%d",&VARIABLE);}

int main(void) { 
int i, j, nMatr, jRow;
 double **triMatr;
 time_t t;
 srand((unsigned int) time(&t));

 READIn(nMatr);
 triMatr = (double **)calloc(nMatr,sizeof(double *));
 for(i = 0; i < nMatr; i++)
   { jRow = (i < nMatr ? i+1 : nMatr);
     triMatr[i]=(double *)calloc(jRow,sizeof(double));
     
for (j = 0; j < jRow; j++)
triMatr[i][j] = (12*(double)rand()/RAND_MAX);
   }
 printf("\n  Result (triangular matrix): ");
 for(i = 0; i < nMatr; i++) { printf("\n ");
     jRow = (i < nMatr ? i+1 : nMatr);
 for (j = 0; j < jRow; j++)
    printf(" %5.2f",triMatr[i][j]);
free (triMatr[i]); }
free (triMatr);

	printf("\n\n Press any key: ");
	_getch(); 
     return 0; }

В программе применена препроцессорная директива #define... – макрос для ввода размерности матрицы. Применение макросов требует к себе внимания и осторожности.

В программе применен указатель double **triMatr на массив указателей. В связи с этим определено двойное обращение к функции calloc(), с помощью которой выполняется динамическое распределение памяти. Следует обратить внимание также на то, что в программе дважды используется функция free() для освобождения выделенной памяти.

Возможный результат выполнения программы показан на рис. 9.2.

Рис. 9.2. Динамическое формирование нижней треугольной матрицы

Задание 2

1. Строки нижней треугольной матрицы заполните числами, равными номерам строк, т.е. число 1 – в первой строке, число 2 – во второй строке, число 3 – в третьей строке и т.д.
2. Оператор условия ? замените на другой оператор.
3. Заполнение матрицы сделайте целыми случайными числами, равномерно распределенными из интервала [–2*Х; 2*Х], где Х – номер компьютера, за которым выполняется лабораторная работа.
4. Напишите программу с динамическим формированием треугольной матрицы из данной прямоугольной матрицы.
5. Напишите программу динамического формирования верхней треугольной матрицы.
6. В приведенной программе предусмотрите вывод матрицы, в которой ниже главной диагонали (и сама диагональ) расположены случайные числа, а выше главной диагонали будут располагаться нули.

Пример 3. Напишите программу заполнения одномерного массива случайными числами, распределенными по стандартному нормальному закону. Размерность массива вводится с клавиатуры пользователем.

Для решения примера выберем метод Марсальи–Брея [9.3]. Его этапы:

1. Генерируются два равномерно распределенных случайных числа 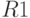, из интервала [0;1].
2. Формируются два соотношения: .
3. Составляется сумма: .
4. Если , то пункты 1–3 повторяются.
5. Если S < 1, то вычисляется первая пара случайных чисел , :
6. , .

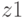Примечание. Нормальный закон характеризуется двумя параметрами: математическим ожиданием и среднеквадратическим отклонением (плюс корень квадратный из дисперсии), которые соответственно равны 0 и 1.

Для оценки математического ожидания используется среднее значение данного объема n выборки случайных чисел. Для оценки дисперсии D могут быть использованы следующие формулы:

где m – среднее значение заданного массива.

Программный код решения примера:

#include <stdio.h>
#include <conio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>

int main(void)
{
double *Norm, *Norm2;
double R1, R2, z1, z2, V1, V2, S;
 int i, j, n;
 time_t t;
 srand((unsigned) time(&t));
 printf("\n\t Enter the size of the array: ");
 scanf_s("%d", &n);
 // Выделение памяти для заданного массива данных
  Norm = (double *)malloc(n*sizeof(double));
  Norm2 = (double *)malloc(n*sizeof(double));
  // Реализация алгоритма метода Марсальи-Брея
  S = 1.0;
  for (i = j = 0; i < n; ++i, ++j){
     while (S >= 1.0) {
  
  R1 = (double) rand()/RAND_MAX;
  R2 = (double) rand()/RAND_MAX;
  V1 = 2.0*R1 - 1.0;
  V2 = 2.0*R2 - 1.0;
  S = (V1*V1 + V2*V2);
  }
z1 = V1 * sqrt(-2.0*log(S)/S);
z2 = V2 * sqrt(-2.0*log(S)/S);
Norm[i] = z1;
Norm2[j] = z2;
S = 1.0; 
}
  // Вывод нормально распределенных случайных чисел
 printf("\n\t Normally distributed random numbers:\n");
 for(i = j = 0; i < n; i++, j++)
 {printf("\n\t %8.4f",Norm[i]);printf("\n\t %8.4f",Norm2[j]);}
 
// Освобождение памяти
 free (Norm);
 free (Norm2);

	printf("\n\n Press any key: ");
	_getch();
	return 0; }

Возможный результат выполнения программы показан на рис. 9.3.

Рис. 9.3. Динамическое формирование нижней треугольной матрицы