НОУ ИНТУИТ | Основы теории вероятностей. Лекция 2: Условная вероятность. Теоремы сложения и умножения вероятностей

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 28.04.2012 | Уровень: специалист | Доступ: свободно

|

Вам нравится? Нравится 32 студентам

| Поделиться |

Поддержать программу

Теоремы сложения и умножения вероятностей

Сформулируем основные теоремы сложения и умножения вероятностей.

Теорема сложения вероятностей. Вероятность суммы двух независимых событий равна сумме вероятностей этих событий

$P(A+B)= P(A)+P(B)$

Замечание. Эта теорема распространяется на произвольное количество независимых событий.

Теорема умножения вероятностей. Вероятность произведения двух независимых событий равна произведению вероятностей появления каждого из этих событий

$P(A \cdot B)= P(A) \cdot P(B)$

Теорема умножения вероятностей для зависимых событий. Вероятность произведения двух зависимых событий называется произведение вероятности наступления одного из событий на условную вероятность наступления второго события 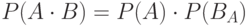$P(A \cdot B)=P(A) \cdot P(B_{A})$

Определение. Суммой событий 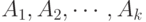$A_{1},A_{2},\cdots , A_{k}$ называется такое событие В, которое состоит в наступлении хотя бы одного события $A_{i}$ .

$B= A_{1},A_{2},\cdots , A_{k} = \sum\limits_{i=1}^k A_{i}$

Определение. Произведением событий 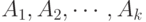$A_{1},A_{2},\cdots , A_{k}$ называется такое событие В, которое состоит в одновременном появлении всех событий

$B= A_{1} \cdot A_{2} \cdot \cdots \cdot A_{k} = \prod\limits_{i=1}^k A_{i}$

Пример 5. Два стрелка стреляют одновременно по мишени. Найти вероятности, что ...

оба промахнулись;
оба попали;
попал один из стрелков;
попал хотя бы один из стрелков,

если вероятность попадания у первого стрелка 0,7, а у второго 0,8.

Решение. Составим таблицу возможных исходов, введя обозначения попал "+", промазал "-"

Таблица возможных исходов
Стрелок 1	Попал	Попал	Не попал	Не попал
Стрелок 2	Попал	Не попал	Попал	Не попал

Т.е. из таблицы видим, что всего 4 вероятных исхода. Других вариантов нет. Ответим теперь на вопросы.

а) Оба стрелка промахнулись, т.е. оба события "промах первого стрелка" и "промах второго стрелка" наступили одновременно, поэтому воспользуемся теоремой умножения вероятностей

$\overline {P(A)} =\overline {P(A_{1})} \cdot \overline {P(A_{2})}= (1-0,7) \cdot (1-0,8) = 0,3 \cdot 0,2 = 0,06$

б) Аналогично рассуждая относительно попадания, получим

$P(A) = P(A_{1}) \cdot P(A_{2})= 0,7 \cdot 0,8 = 0,56$

в) В этом случае следует воспользоваться теоремой сложения вероятностей, так как из таблицы видно, что это два взаимоисключающих исхода:

попал первый стрелок, то второй промахнулся,
если попал второй стрелок, то первый промахнулся.

$P(B) = P(A_{1}) \cdot \overline P(A_{2}) + P(A_{2}) \cdot \overline P(A_{1}) = 0,7 \cdot (1-0,8) +0,8 \cdot (1-0,7) =0,7 \cdot 0,2 +0,8 \cdot 0,3 =0,38$

г) В этом случае нас не интересует только один исход испытаний, когда промахнулись оба, поэтому ответ можно найти как

$P(C)=1-\overline {P(A)}=1-0,06=0,94 ,$

или, перебирая последовательно все возможные варианты исходов,

$P(C)=P(A_{1}) \cdot P(A_{2}) +\overline {P(A_{1})} \cdot P(A_{2}) +\overline {P(A_{2})} \cdot P(A_{1}) =0,7 \cdot 0,8 + (1-0,7) \cdot 0,8+(1-0,8) \cdot 0,7 =0,94$

Дальше >>

Авторизоваться

Основы теории вероятностей

Условная вероятность. Теоремы сложения и умножения вероятностей

Теоремы сложения и умножения вероятностей

Вопросы и ответы