|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Описание неопределенностей в теории принятия решений
Анализ интервальных данных
Перспективная и быстро развивающаяся область исследований последних десятилетий - анализ интервальных данных. Речь идет о развитии методов прикладной математической статистики в ситуации, когда статистические данные - не числа, а интервалы, в частности, порожденные наложением ошибок измерения на значения случайных величин. Приведем основные идеи весьма перспективного для вероятностно-статистических методов и моделей принятия решений асимптотического направления в статистике интервальных данных.
В настоящее время признается необходимым изучение устойчивости (робастности) оценок параметров к малым отклонениям исходных данных и предпосылок модели. Однако популярная среди теоретиков модель засорения (модель Тьюки-Хьюбера) представляется не вполне адекватной. Эта модель нацелена на изучение влияния больших "выбросов". Поскольку любые реальные измерения лежат в некотором фиксированном диапазоне, а именно, заданном в техническом паспорте средства измерения, то зачастую выбросы не могут быть слишком большими.
В одной из таких схем изучается влияние интервальности исходных данных на статистические выводы. Необходимость такого изучения стала очевидной следующим образом. В государственных стандартах СССР по прикладной статистике в обязательном порядке давалось справочное приложение "Примеры применения правил стандарта". При разработке ГОСТ 11.011-83 были переданы для анализа реальные данные о наработке резцов до предельного состояния (в часах). Оказалось, что все эти данные представляли собой либо целые числа, либо полуцелые (т.е. после умножения на 2 становящиеся целыми). Ясно, что исходная длительность наработок искажена. Необходимо учесть в статистических процедурах наличие такого искажения исходных данных. Как это сделать?
Первое, что приходит в голову - модель группировки данных, согласно которой для истинного значения Х проводится замена на ближайшее число из множества {0,5n, n=1,2,3,...} . Однако эту модель целесообразно подвергнуть сомнению, а также рассмотреть иные модели. Так, возможно, что Х надо приводить к ближайшему сверху элементу указанного множества - если проверка качества поставленных на испытание резцов проводилась раз в полчаса. Другой вариант: если расстояния от Х до двух ближайших элементов множества {0,5n, n=1,2,3,...} примерно равны, то естественно ввести рандомизацию при выборе заменяющего числа, и т.д.
Целесообразно построить новую математико-статистическую модель, согласно которой результаты наблюдений - не числа, а интервалы Например, если в таблице приведено значение 53,5, то это значит, что реальное значение - какое-то число от 53,0 до 54,0, т.е. какое-то число в интервале [53,5 - 0,5; 53,5 + 0,5] , где 0,5 - максимально возможная погрешность. Принимая эту модель, мы попадаем в новую научную область - статистику интервальных данных. Статистика интервальных данных идейно связана с интервальной математикой, в которой в роли чисел выступают интервалы . Это направление математики является дальнейшим развитием известных правил приближенных вычислений, посвященных выражению погрешностей суммы, разности, произведения, частного через погрешности тех чисел, над которыми осуществляются перечисленные операции.
В интервальной математике сумма двух интервальных чисел [a,b] и [c,d] имеет вид [a,b] + [c,d] = [a+c, b+d] , а разность определяется по формуле ![[a,b] - [c,d] = [a-d, b-c]](/sites/default/files/tex_cache/88b7d9952a23cd83c1f6541214408a67.png) . Для положительных a, b, c, d произведение определяется формулой
. Для положительных a, b, c, d произведение определяется формулой ![[a,b] * [c,d] = [ac, bd]](/sites/default/files/tex_cache/3d9faa8a97e3a7728b214e213cc7d487.png) , а частное имеет вид
, а частное имеет вид ![[a,b] / [c,d] = [a/d, b/c]](/sites/default/files/tex_cache/4205578a1cd5dc528b87204aa9895d85.png) . Эти формулы получены при решении соответствующих оптимизационных задач. Пусть х лежит в отрезке
. Эти формулы получены при решении соответствующих оптимизационных задач. Пусть х лежит в отрезке ![[a,b]](/sites/default/files/tex_cache/edf97e7650f93d7606ba4990a3a8f251.png) , а у - в отрезке
, а у - в отрезке ![[c,d]](/sites/default/files/tex_cache/86cf196d6eb91b6894bb4aa0e9342442.png) . Каково минимальное и максимальное значение для
. Каково минимальное и максимальное значение для  ? Очевидно,
? Очевидно, 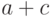 и
и  соответственно. Минимальные и максимальные значения для х-у, ху, х/у задают нижние и верхние границы для интервальных чисел, задающих результаты арифметических операций. А от арифметических операций можно перейти ко всем остальным математическим алгоритмам. Так строится интервальная математика. К настоящему времени удалось решить, в частности, ряд задач теории интервальных дифференциальных уравнений, в которых коэффициенты, начальные условия и решения описываются с помощью интервалов.
соответственно. Минимальные и максимальные значения для х-у, ху, х/у задают нижние и верхние границы для интервальных чисел, задающих результаты арифметических операций. А от арифметических операций можно перейти ко всем остальным математическим алгоритмам. Так строится интервальная математика. К настоящему времени удалось решить, в частности, ряд задач теории интервальных дифференциальных уравнений, в которых коэффициенты, начальные условия и решения описываются с помощью интервалов.
В настоящем разделе обсуждаем асимптотические методы статистического анализа интервальных данных при больших объемах выборок и малых погрешностях измерений. В отличие от классической математической статистики, сначала устремляется к бесконечности объем выборки и только потом - уменьшаются до нуля погрешности. В частности, еще в начале 1980-х годов с помощью такой асимптотики были сформулированы правила выбора метода оценивания в ГОСТ 11.011-83.
Разработана общая схема исследования, включающая расчет нотны (максимально возможного отклонения статистики, вызванного интервальностью исходных данных) и рационального объема выборки (превышение которого не дает существенного повышения точности оценивания). Она применена к оцениванию математического ожидания и дисперсии, медианы и коэффициента вариации, параметров гамма-распределения и характеристик аддитивных статистик, при проверке гипотез о параметрах нормального распределения, в т.ч. с помощью критерия Стьюдента, а также гипотезы однородности с помощью критерия Смирнова. Изучено асимптотическое поведение оценок метода моментов и оценок максимального правдоподобия (а также более общих - оценок минимального контраста), проведено асимптотическое сравнение этих методов в случае интервальных данных, найдены общие условия, при которых, в отличие от классической математической статистики, метод моментов дает более точные оценки, чем метод максимального правдоподобия.
Разработаны подходы к рассмотрению интервальных данных в основных постановках регрессионного, дискриминантного и кластерного анализов. В частности, изучено влияние погрешностей измерений и наблюдений на свойства алгоритмов регрессионного анализа, разработаны способы расчета нотн и рациональных объемов выборок, введены и исследованы новые понятия многомерных и асимптотических нотн, доказаны соответствующие предельные теоремы. Начата разработка интервального дискриминантного анализа, в частности, рассмотрено влияние интервальности данных на показатель качества классификации.
В области асимптотической математической статистики интервальных данных мы имеем мировой приоритет. Очевидно, со временем во все виды статистического программного обеспечения должны быть включены алгоритмы интервальной статистики, "параллельные" обычно используемым алгоритмам прикладной математической статистики. Это позволит в явном виде учесть наличие погрешностей у результатов наблюдений, сблизить позиции метрологов и статистиков.
Многие из утверждений статистики интервальных данных весьма отличаются от аналогов из классической математической статистики. В частности, не существует состоятельных оценок; средний квадрат ошибки оценки, как правило, асимптотически равен сумме дисперсии оценки, рассчитанной согласно классической теории, и некоторого положительного числа (равного квадрату т.н. нотны - максимально возможного отклонения значения статистики из-за погрешностей исходных данных) - в результате метод моментов оказывается иногда точнее метода максимального правдоподобия; нецелесообразно увеличивать объем выборки сверх некоторого предела (называемого рациональным объемом выборки) - вопреки классической теории, согласно которой чем больше объем выборки, тем точнее выводы.
Развитие идей статистики интервальных данных продолжается уже в течение более чем 25 лет, и еще много чего надо сделать!
