Деревья, вероятность и генетика
Вероятность и генетика
Приведем примеры использования деревьев в генетике. С помощью дерева можно
наглядно представить наследование пары генов  и
и  ,
передаваемых родителями. Потомок получает эти гены в одной из комбинаций:
,
передаваемых родителями. Потомок получает эти гены в одной из комбинаций: 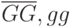 или
или 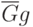 .
Генетически комбинация
.
Генетически комбинация  не
отличается от комбинации
не
отличается от комбинации  .
.
В генетике допускается, что наследование данного гена происходит случайно,
независимо и с равными вероятностями для всех потомков (у растений,
например, их может быть очень много). Пусть ген  наследуется (и
от отца, и от матери) с вероятностью
наследуется (и
от отца, и от матери) с вероятностью  , ген
, ген  — с вероятностью
— с вероятностью  .
В этом случае отца в смысле унаследования гена можно уподобить, например,
одной бросаемой монете, мать — второй (рис. 13.3).
Тогда
.
В этом случае отца в смысле унаследования гена можно уподобить, например,
одной бросаемой монете, мать — второй (рис. 13.3).
Тогда 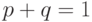 .
.
Далее будем полагать, что 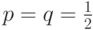 . Заметим, что у
таких
"генеалогических" деревьев вершины, если они не висячие и не
корневые,
имеют степень 3.
. Заметим, что у
таких
"генеалогических" деревьев вершины, если они не висячие и не
корневые,
имеют степень 3.
Теперь от родителей перейдем к "дедушкам" и "бабушкам" и продлим дерево еще на один ярус.
Когда сочетаются браком двоюродные брат и сестра, они могут передать своему ребенку копии пар генов, которыми обладали их общие дедушка и бабушка (возможными мутациями этих генов пренебрегаем).
Считая, что в общем случае неизвестно численное значение
вероятности  того, что потомок наследует от своих
родителей пару
одинаковых генов
того, что потомок наследует от своих
родителей пару
одинаковых генов  или
или 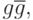 определим в
зависимости от
определим в
зависимости от  вероятность унаследования общей пары генов
от
общего дедушки.
вероятность унаследования общей пары генов
от
общего дедушки.
Граф, описывающий ситуацию, которая нас интересует, в случаях так называемого кровного родства деревом не является — две его висячие вершины "слипаются" (рис. 13.4).
Введем коэффициент кровного родства по формуле 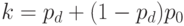 ,
где
,
где 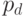 — вероятность того, что оба гена
— вероятность того, что оба гена  являются копиями генов
являются копиями генов  . При этом оказывается, что
вероятность
. При этом оказывается, что
вероятность 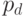 нетрудно
подсчитать.
нетрудно
подсчитать.
Рассмотрим один из генов, который  унаследовал от своего
отца
унаследовал от своего
отца  .
Вероятность того, что
.
Вероятность того, что  унаследовал этот ген от своего деда
унаследовал этот ген от своего деда  ,
равна
,
равна  . Вероятность того, что дедушка передал копию
того же
гена
. Вероятность того, что дедушка передал копию
того же
гена  , также равна
, также равна  , и вероятность
того, что
, и вероятность
того, что  передал
копию этого гена
передал
копию этого гена  , равна
, равна  . Все эти
события независимые, и, следовательно,
. Все эти
события независимые, и, следовательно, 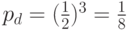 .
.
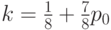 .
.
Рассмотренный пример дает некоторое представление о расчетах, связанных с проблемами сохранения в потомстве желательных признаков прародителей: вывода сортов пшеницы, пород собак, голубей, домашних животных, искусственного восстановления вымирающих пород животных. Все эти проблемы разные по роли и значимости, но они имеют общую математическую суть.


