Разработка математических моделей при проектировании технологии
15.3. Математические модели объектов проектирования на макроуровне
Компонентные и топологические уравнения
Для одного и того же объекта (детали) на микро- и макроуровнях используют разные математические модели. На микроуровне ММ должна отражать внутренние по отношению к объекту процессы, протекающие в сплошных средах. На макроуровне ММ того же объекта служит для отражения только тех его свойств, которые характеризуют взаимодействие этого объекта с другими элементами в составе исследуемой системы [51].
Математические модели элементов на макроуровне получают одним из способов, рассмотренных ранее.
Математические модели систем (ММС) формируют из математических моделей элементов (ММЭ), излагаемых ниже.
Уравнения, входящие в ММЭ, называют компонентными. Наряду с компонентными уравнениями в ММС входят уравнения, отражающие способ связи элементов между собой в составе системы и называемые топологическими. Топологические уравнения могут выражать законы сохранения, условия неразрывности, равновесия и т. д.
В используемых в САПР методах формирования ММС принято моделируемую систему представлять в виде совокупности физически однородных подсистем. Каждая подсистема описывает процессы определенной физической природы, например механические, электрические, тепловые, гидравлические. Как правило, для описания состояния одной подсистемы достаточно применять фазовые переменные двух типов — потенциала и потока.
Особенностью топологических уравнений является то, что каждое из них связывает однотипные фазовые переменные, относящиеся к разным элементам системы. Примером могут служить уравнения законов Кирхгофа, записываемые относительно либо токов, либо напряжений ветвей. Для компонентных уравнений характерно то, что они связывают разнотипные фазовые переменные, относящиеся к одному элементу. Например, уравнение закона Ома связывает ток и напряжение резистора.
Формы представления моделей
Элементы подсистем бывают простыми и сложными. Элемент называют простым, если соответствующая ему ММЭ может быть представлена в виде одного линейного уравнения, связывающего переменную типа потенциала U и переменную типа потока I, характеризующие состояние данного элемента.
В физически однородных подсистемах различают три типа простых элементов. Это элементы емкостного, индуктивного и резистивного типов. Соответствующие им ММЭ имеют вид
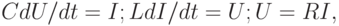 |
( 15.13) |
где С, L, U, I — параметры элементов.
Элементы подсистем в зависимости от числа однотипных фазовых переменных, входящих в ММЭ, делят на двухполюсники и многополюсники. Двухполюсник характеризуется парой переменных типа U и I, определяется так же, как простой элемент, если снять условие линейности уравнения. Многополюсник можно представить как совокупность взаимосвязанных двухполюсников.
Для представления математических моделей на макроуровне применяют несколько форм.
Инвариантная форма — представление модели в виде системы уравнений, записанной на общепринятом математическом языке, безотносительно к методу численного решения. Применительно к системам обыкновенных дифференциальных уравнений различают две инвариантные формы: нормальную и общую, определяемые тем, в каком виде — явном или неявном относительно вектора производных — представлена система.
Ряд форм модели получается при преобразовании ее уравнений на основе формул и требований выбранного численного метода решения. Так, численное решение дифференциальных уравнений как в частных производных, так и в обыкновенных требует их предварительного преобразования — дискретизации и алгебраизации. Дискретизация заключается в замене непрерывных независимых переменных (времени и пространственных координат) дискретным множеством их значений.
Алгебраизованная форма — результат представления дифференциальных уравнений в полученных после дискретизации точках в алгебраизованном виде с помощью формул численного интегрирования. Ряд численных методов решения основан на линеаризации исходных уравнений.
Линеаризованная форма модели — представление уравнений в линейном виде. Алгебраизация и линеаризация могут осуществляться по отношению ко всем или только к избранным переменным, уравнениям или их частям, что увеличивает разнообразие возможных форм представления моделей.
Формы представления моделей определяются также используемыми языковыми средствами. Наряду с традиционным математическим языком применяют алгоритмические языки, а также те или иные графические изображения. Рассмотрим особенности представления моделей в виде эквивалентных схем.
Последние облегчают пользователю восприятие модели и приводят к представлению модели в той или иной схемной форме, например представление моделей в виде эквивалентных схем, графов. К таким формам относится также представление разностных уравнений с помощью шаблонов.
В разных областях техники применяют специфические системы обозначений элементов на эквивалентных схемах. Будем использовать в дальнейшем единую систему обозначений для элементов всех подсистем, обычно применяемую при изображении электрических эквивалентных схем. При этом элементы представляют собой двухполюсники, которые могут быть пяти различных видов, их условные обозначения приведены на рис. 15.1а.
Получение эквивалентных схем — обычная для инженеров-схемотехников операция, выполняемая при анализе функционирования радиоэлектронных устройств. Переход от принципиальной электрической схемы к эквивалентной заключается в замене обозначений электронных приборов обозначениями двухполюсников ( рис. 15.1а) и добавлении ветвей, отображающих учитываемые паразитные параметры. Не вызывает затруднений и составление на основе электрогидравлических и электротепловых аналогий эквивалентных схем, отражающих гидравлические, пневматические и тепловые процессы в проектируемых устройствах.
Составление эквивалентных схем для механических систем начинается с выбора системы координат, начало О которой должно быть связано с инерциальной системой отсчета. Далее формируются п эквивалентных схем, где п — число степеней свободы. В общем случае возможны три эквивалентные схемы, соответствующие поступательным движениям вдоль координатных осей, и три эквивалентные схемы, которые соответствуют вращательным движениям вокруг осей, параллельных координатным осям.
Рассмотрим правила составления эквивалентных схем на примере одной из эквивалентных схем для поступательного движения:
- для каждого тела А% с учитываемой массой Сь в эквивалентной схеме выделяется узел I, и между узлом i и узлом О включается двухполюсник массы С7 ;
- трение между контактируемыми телами Ар и Aq отражается двухполюсником механического сопротивления, включаемым между узлами р и q ;
- пружина, соединяющая тела Ар и Aqy, а также другие упругие взаимодействия контактируемых тел Ар и Aq отражаются двухполюсником гибкости (жесткости), включаемым между узлами р и q.
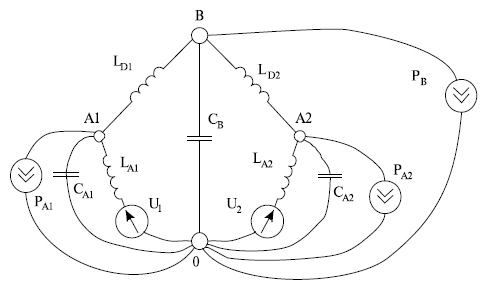
В качестве примера на рис. 15.1в приведена эквивалентная схема, которая моделирует вертикальные скорости и усилия, возникающие в элементах движущегося транспортного устройства — оно условно изображено на рис. 15.1б в виде платформы В и колес А1 и А2. Здесь учитываются массы платформы Св и колес Са, жесткости колес LA и рессор LD, a также веса Рв, Рл1 Рл2 платформы и колес. Внешние воздействия отражены источниками скорости U.
Часто на эквивалентных схемах рядом с обозначением нелинейного элемента указан его тип или записано его компонентное уравнение.
Для отражения взаимосвязей подсистем различной физической природы, из которых состоит моделируемая техническая система, в эквивалентные схемы подсистем вводят специальные преобразовательные элементы. Различают три вида связей подсистем. Трансформаторная и гираторная связи выражают соотношения между фазовыми переменными двух подсистем, этим типам связей соответствуют преобразовательные элементы, представляемые парами источников тока или напряжения. Третий вид связи выражает влияние фазовых переменных одной подсистемы на параметры элементов другой и задается в виде зависимостей С, L или R от фазовых переменных. если для источника объемного расхода в гидравлической подсистеме использовать выражение g — =SV, а для источника силы в механической подсистеме — выражение F = SP, где V — скорость перемещения поршня; S — площадь поршня; Р — давление жидкости в цилиндре.
Примеры математических моделей элементов электронных схем. Для конденсаторов, катушек индуктивности и резисторов чаще всего применяют простые модели (15.13). Примерами сложных элементов являются транзисторы, диоды, трансформаторы.
Контрольные вопросы и задания
- Что представляет собой процедура разработки моделей элементов?
- На чем основаны теоретические методы получения моделей элементов?
- В чем суть экспериментальных методов?
- Поясните идею методики макромоделирования в технологии.
- Поясните преимущества активного эксперимента.
- Что представляет собой диалоговое моделирование?
- Приведите примеры полной модели и макромодели из какой-либо предметной области.
- В чем заключаются основные отличия методов конечных разностей и конечных элементов?
- Приведите пример математической модели какого-либо объекта на микроуровне.
- Что такое область адекватности модели?
- Для задачи теплопередачи в стержне, описываемой одномерным уравнением теплопроводности, запишите систему разностных уравнений при разделении стержня на п участков.
- Для задачи предыдущего пункта разделите стержень на п конечных элементов. Задайтесь линейной аппроксимацией температуры от х (направление оси х выбрано вдоль стержня). Запишите выражения для координатных функций. Выполните алгебраизацию задачи, задавшись видом функционала, характеризующего качество аппроксимации.
- Приведите примеры компонентных и топологических уравнений для произвольной электронной схемы.
- Запишите компонентные уравнения преобразовательного элемента, отображающего связь электрической и механической подсистем в электромагните.
- Какими уравнениями описывают электрическую модель?
- Что представляет собой двухполюсник?
- Что представляет собой многополюсник?
- Поясните инвариантную форму модели.