Математические модели объектов проектирования РЭС
14.3. Математические модели монтажно-коммутационного пространства
Монтажно-коммутационное пространство (МКП) предназначено для размещения конструктивных модулей и трассировки соединений между их контактами, которые должны быть соединены электрическими цепями. Форма и, естественно, математическая модель МКП зависят от уровня модуля, для которого в данный момент решаются задачи конструирования (базовый матричный кристалл, печатная плата, панель и т. д.). В дальнейшем ограничимся только плоским монтажно-коммутационным пространством, соответствующим конструктивному модулю типа печатной платы.
Без потери общности будем считать, что пространство имеет прямоугольную форму, так как введением областей, в которых запрещается размещение конструктивных модулей более низкого уровня или трассировки соединений, можно придать пространству произвольную форму. Так как МКП служит для решения двух задач — размещения модулей и трассировки, — то модели МКП, используемые для решения каждой задачи, будут иметь отличия. Рассмотрим эти модели подробнее.
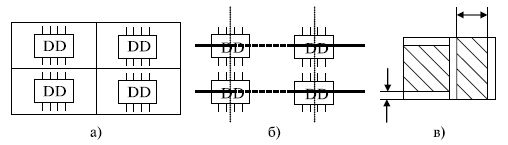
Наибольшее распространение для решения задач размещения конструктивных модулей в плоском МКП получили эвристические дискретные модели. Такие модели (будем их называть МКП1) строятся следующим образом ( рис. 14.3а): МКП разбивается на элементарные площадки (дискреты), каждая из которых предназначена для размещения одного конструктивного модуля более низкого уровня, например микросхемы на печатной плате. Эти площадки в дальнейшем будем называть дискретами рабочего поля (ДРП).
Каждый дискрет в процессе решения задачи размещения может находиться в одном из следующих состояний: свободен для размещения, занят, имеет определенный вес, запрещающий размещение в нем модуля, и т. д. Такая модель МКП отличается простотой и удобством использования в эвристических алгоритмах размещения, однако она не является полностью формализованной.
Одной из разновидностей модели МКП1 является модель с ортогональной сеткой, в узлах которой могут размещаться модули низкого уровня ( рис. 14.3б). Шаг сетки выбирается из условия возможности размещения модулей в соседних узлах сетки.
При размещении разногабаритных компонентов часто размер ДРП выбирают равным наибольшему общему делителю линейных размеров размещаемых модулей либо линейным размерам установочного места для наименьшего из модулей, если размеры всех модулей кратны. Заметим, что выбор шага дискретизации представляется весьма важным, так как при малых размерах ДРП увеличивается время решения задачи, зато повышается плотность заполнения МКП модулями низшего уровня.
Аналогичные дискретные модели используются и для решения задач трассировки. В этом случае дискрет является квадратом со сторонами, равными ширине проводника плюс зазор между ними ( рис. 14.3в). При этом считается, что проводник из каждого дискрета может быть проведен только в соседний ДРП.
Наибольшее распространение для решения задач размещения получили модели МКП в виде взвешенного графа VG(S, V), которые будем обозначать МКП2. Взвешенный граф VG представляет собой симметрический граф, в котором множество вершин S соответствует множеству установочных позиций в коммутационном пространстве для модулей низшего уровня, а множество ветвей интерпретирует множество связей между соответствующими установочными позициями. Каждой ветви графа uij присваивается вес pij — он равен числу условных единиц расстояния между центрами установочных позиций Si и Sj, интерпретируемых вершинами, которые инцидентны данной ветви. Вес ветви pij определяется в зависимости от метрики пространства по одной из формул (14.1, 14.2).
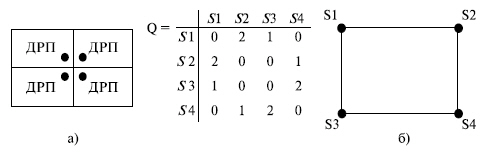
Для описания взвешенного графа VG удобно использовать матрицу смежностей Q, строки и столбцы которой соответствуют вершинам графа, т. е. множеству установочных позиций в МКП, а элементы gij равны весу ветви, инцидентной i -й и j -й вершинам графа. Элементы, лежащие на главной диагонали матрицы смежностей Q, принимаются равными нулю. Так, для МКП, показанного на рис. 14.3а, модель в виде взвешенного графа при ортогональной матрице смежности Q имеет вид как на рис. 14.4. Для решения задач размещения применяются и другие графовые модели.
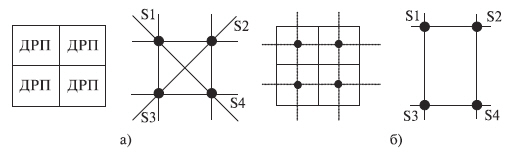
Большими возможностями для формализации процесса трассировки обладают комбинированные дискретно-графовые модели МКПЗ. В этом случае МКП моделируется симметрическим графом G(S, V), в котором каждому ДРП ставится в соответствие вершина графа. Вершины Si, и Sj соединяются ветвью, если они соответствуют соседним дискретам, через которые может проходить проводник. Трассы проводников могут проходить только по ветвям графа, а длина трасс определяется в соответствии с выбранной метрикой пространства. На рис. 14.5а показаны модели МКП2 для трассировки по ортогональным направлениям и при допущении трассировки под углом в 45° (трассировка по шести направлениям).
Симметрический граф G(S, V) с множеством вершин S и множеством ветвей V может быть описан в ЭВМ матрицей инциденций А, элемент которой ai,j = 1, если вершина Si инцидентна ветви ui,j, и ai,j = 0 — в противном случае. Для графа, показанного на рис. 14.5а при допущении трассировки по восьми направлениям матрица инциденций имеет вид ( рис. 14.5).
Модель МКПЗ очень широко распространена и позволяет при трассировке получить все множество кратчайших путей в отличие от МКП1, в которой обычно получают лишь один из возможных путей из этого множества. Кроме того, вводя вес для вершин и ветвей графа, можно регулировать скорость распространения числовой волны по определенным направлениям в волновых алгоритмах трассировки засчет введения соответствующих задержек.
Аналогична МКПЗ и графовая модель пространства МКП4, также используемая для решения задач трассировки. Модель МКП4 представляет симметрический граф G(S,V), вершины которого Si соответствуют узлам координатной сетки, нанесенной на плоское МКП, а ветви графа ui,j — отрезкам координатной сетки, соединяющим две соседние точки ( рис. 14.5б). Особенностью модели МКП4 по сравнению с МКПЗ является интерпретация ветви графа G(S, V) как элементарного отрезка проводника, который может быть проложен в этом месте МКП. По своим возможностям модель МКП4 эквивалентна МКПЗ.
Для моделирования коммутационного пространства при решении задач трассировки можно использовать модели в виде мультиграфа, т. е. симметрического графа, у которого существует хотя бы одна пара вершин, соединенных несколькими ветвями. Ветви, соединяющие одну и ту же пару вершин, называют кратными, а их максимальное число — мультичислом графа.
Одна из таких моделей МКП5 представляет мультиграф MG(S, V), в котором множество вершин графа S соответствует множеству установочных позиций в коммутационном пространстве для модулей низшего уровня. Множество ветвей V соответствует множеству взаимно независимых непосредственных переходов между установочными позициями, т. е. множеству областей, допускающих трассировку соединений между этими позициями без пересечений. Мультиграф MG(S, V) может быть описан с помощью матрицы смежности Q, в которой, как и для взвешенного графа, элементы gi,j, лежащие на главной диагонали, принимаются равными нулю, а внедиагональные элементы gi,j равны числу кратных ветвей, инцидентных i -й и j -й вершинам графа. Для примера на рис. 14.5 показаны фрагмент коммутационного пространства с установочными позициями и его модель в виде мультиграфа при допущении трассировки без пересечений трех проводников между соседними позициями.
Еще более общей моделью МКП в виде мультиграфа, используемой для решения задач трассировки, является модель МКП6, в которой вершины графа соответствуют макродискретам, на которые разбивается МКП. Ребра мультиграфа соединяют соседние вершины, причем количество кратных ветвей определяется тем, сколько проводников может пройти через границы соседних дискретов.
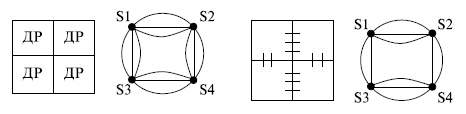
Расстояние определяется как количество макродискретов, пройденных проводником при трассировке. Пример фрагмента МКП с макродискретами, через границы которых допускается прохождение трех и двух проводников, и соответствующий ему мультиграф показаны на рис. 14.6.
Матрица смежности такого мультиграфа имеет вид
Модель МКП6 предполагает проведение трассировки проводников в два этапа: на первом определяется путь с точностью до вершины мультиграфа (макродискрета), на втором — путь конкретизируется с точностью до ветви. Это позволяет на первом этапе выбрать наилучшее взаимное расположение трасс, а на втором провести собственно трассировку, что уменьшает зависимость количества реализованных в коммутационном пространстве трасс от очередности трассировки.
Контрольные вопросы и упражнения
- Что называется математической моделью (ММ)?
- Что называют внутренними, внешними и выходными параметрами ММ?
- Что называют фазовыми переменными?
- Что называют базисным вектором?
- Покажите общий вид системы уравнений для любой РЭС и дайте пояснения.
- Что включается в анализ ММ?
- Что представляют собой компонентные уравнения и компонентная модель?
- Какие требования предъявляют к ММ объекта?
- На какие группы делятся макромодели?
- Для чего предназначена факторная модель?
- Для чего предназначена фазовая модель?
- Как получают физическую модель?
- Как получают формальную модель?
- В чем различие статической и динамической моделей?
- В чем заключается модульный принцип конструирования?
- Приведите иерархию конструктивных модулей.