Растровое преобразование графических примитивов

Алгоритмы заполнения областей

Для заполнения областей, ограниченных замкнутой линией, применяются два основных подхода: затравочное заполнение и растровая развертка.

Методы первого типа исходят из того, что задана некоторая точка (затравка) внутри контура и задан критерий принадлежности точки границе области (например, задан цвет границы). В алгоритмах ищут точки, соседние с затравочной и расположенные внутри контура. Если обнаружена соседняя точка, принадлежащая внутренней области контура, то она становится затравочной и поиск продолжается рекурсивно.

Методы растровой развертки основаны на сканировании строк растра и определении, лежит ли точка внутри заданного контура области. Сканирование осуществляется чаще всего "сверху вниз", а алгоритм определения принадлежности точки заданной области зависит от вида ее границы.

Сначала рассмотрим простой алгоритм заполнения с затравкой с использованием стека. Под стеком в данном случае мы будем понимать массив, в который можно последовательно помещать значения и последовательно извлекать, причем извлекаются элементы не в порядке поступления, а наоборот: по принципу "первым пришел - последним ушел" ("first in - last out"). Алгоритм заполнения выглядит следующим образом:

Поместить затравочный пиксель в стек
Пока стек не пуст:
	Извлечь пиксель из стека
	Инициализировать пиксель
	Для каждого из четырех соседних пикселей:
		Проверить, является ли он граничным и был ли он инициализирован
		Если нет, то поместить пиксель в стек

Алгоритм можно модифицировать таким образом, что соседними будут считаться восемь пикселей (добавляются элементы, расположенные в диагональном направлении).

Методы растровой развертки рассмотрим сначала в применении к заполнению многоугольников. Простейший метод построения состоит в том, чтобы для каждого пикселя растра проверить его принадлежность внутренности многоугольника. Но такой перебор слишком неэкономичен, поскольку фигура может занимать лишь незначительную часть экрана, а геометрический поиск - задача трудоемкая, сопряженная с длинными вычислениями. Алгоритм станет более эффективным, если предварительно выявить минимальный прямоугольник, в который погружен контур многоугольника, но и этого может оказаться недостаточно.

В случае, когда многоугольник, ограничивающий область, задан списком вершин и ребер (ребро определяется как пара вершин), можно предложить еще более экономный метод. Для каждой сканирующей строки определяются точки пересечения с ребрами многогранника, которые затем упорядочиваются по координате . Определение того, какой интервал между парами пересечений есть внутренний для многогранника, а какой нет, является достаточно простой логической задачей. При этом если сканирующая строка проходит через вершину многогранника, то это пересечение должно быть учтено дважды в случае, когда вершина является точкой локального минимума или максимума. Для поиска пересечений сканирующей строки с ребрами можно использовать алгоритм Брезенхема построения растрового образа отрезка.

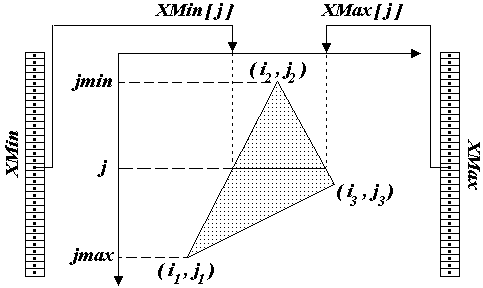
В заключение в качестве примера приведем алгоритм закраски внутренней области треугольника, основанный на составлении полного упорядоченного списка всех отрезков, составляющих этот треугольник. Для записи горизонтальных координат концов этих отрезков будем использовать два массива и размерностью, равной числу пикселей растра по вертикали (рис. 8.11).

Построение начинается с инициализации массивов и : массив заполняется нулями, а массив - числом , равным числу пикселей растра по горизонтали. Затем определяем значения 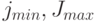, ограничивающие треугольник в вертикальном направлении. Теперь, используя модифицированный алгоритм Брезенхема, занесем границы отрезков в массивы и . Для этого всякий раз при переходе к очередному пикселю при формировании отрезка вместо его инициализации будем сравнивать его координату с содержимым -й ячейки массивов. Если , то записываем координату в массив . Аналогично при условии координату записываем в массив .

Если теперь последовательно применить алгоритм Брезенхема ко всем трем сторонам треугольника, то мы получим нужным образом заполненные массивы границ. Остается только проинициализировать пиксели внутри отрезков .

Этот алгоритм можно легко распространить на случай произвольного выпуклого многоугольника.

Рис. 8.11. Схема построения растровой развертки треугольника

Вопросы и упражнения

1. Что такое разложение в растр?
2. Какова математическая основа растрового разложения в алгоритме Брезенхема?
3. По какому критерию инициализируется пиксель в этом алгоритме?
4. Чем отличаются ветви алгоритма при углах наклона <45 и >45 ?
5. Какую часть окружности достаточно построить, чтобы затем путем отражений получить окружность целиком?
6. Какую часть эллипса достаточно построить, чтобы затем путем отражений получить эллипс целиком?
7. Назовите два типа алгоритмов заполнения областей.
8. Какая структура данных используется в алгоритмах с затравкой?
9. Какие данные используются при построении растровой развертки треугольника?