Удаление невидимых поверхностей и линий
Алгоритм Варнока
В отличие от алгоритма Робертса, Варнок в 1968 г. предложил алгоритм, работающий не в объектном пространстве, а в пространстве образа. Он также нацелен на изображение многогранников, а главная идея его основана на гипотезе о способе обработки информации, содержащейся в сцене, глазом и мозгом человека. Эта гипотеза заключается в том, что тратится очень мало времени и усилий на обработку тех областей, которые содержат мало информации. Большая часть времени и труда затрачивается на области с высоким информационным содержимым. Так, например, рассматривая помещение, в котором имеется только картина на стене, мы быстро осматриваем стены, пол и потолок, а затем все внимание сосредоточиваем на картине. В свою очередь, на этой картине, если это портрет, мы бегло отмечаем фон, а затем более внимательно рассматриваем лицо изображенного персонажа, в особенности глаза, губы. Как правило, достаточно детально рассматриваются еще и руки и с чуть меньшим вниманием - одежда.
В алгоритме Варнока и его вариантах делается попытка воспользоваться тем, что большие области изображения однородны. Такое свойство называют когерентностью, имея в виду, что смежные области (пиксели) вдоль обеих осей х и у имеют тенденцию к однородности.
В пространстве изображения рассматривается окно и решается вопрос о том, пусто ли оно, или его содержимое достаточно просто для визуализации. Если это не так, то окно разбивается на фрагменты до тех пор, пока содержимое фрагмента не станет достаточно простым для визуализации или его размер не достигнет требуемого предела разрешения. В последнем случае информация, содержащаяся в окне, усредняется, и результат изображается с одинаковой интенсивностью или цветом.
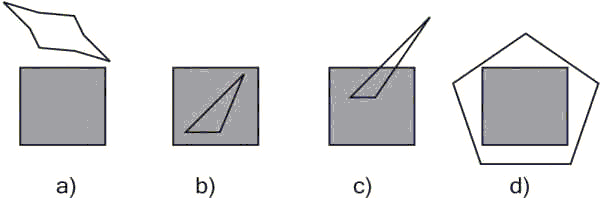
Конкретная реализация алгоритма Варнока зависит от метода разбиения окна и от деталей критерия, используемого для того, чтобы решить, является ли содержимое окна достаточно простым. В оригинальной версии алгоритма каждое окно разбивалось на четыре одинаковых подокна. Многоугольник, входящий в изображаемую сцену, по отношению к окну будем называть (рис. 6.3)
- внешним, если он целиком находится вне окна;
- внутренним, если он целиком расположен внутри окна;
- пересекающим, если он пересекает границу окна;
- охватывающим, если окно целиком расположено внутри него.
Теперь можно в самом общем виде описать алгоритм.
Для каждого окна:
- Если все многоугольники сцены являются внешними по отношению к окну, то оно пусто; изображается фоновым цветом и дальнейшему разбиению не подлежит.
- Если только один многоугольник сцены имеет общие точки с окном и является по отношению к нему внутренним, то окно заполняется фоновым цветом, а сам многоугольник заполняется своим цветом.
- Если только один многоугольник сцены имеет общие точки с окном и является по отношению к нему пересекающим, то окно заполняется фоновым цветом, а часть многоугольника, принадлежащая окну, заполняется цветом многоугольника.
- Если только один многоугольник охватывает окно и нет других многоугольников, имеющих общие точки с окном, то окно заполняется цветом этого многоугольника.
- Если существует хотя бы один многоугольник, охватывающий окно, то среди всех таких многоугольников выбирается тот, который расположен ближе всех многоугольников к точке наблюдения, и окно заполняется цветом этого многоугольника.
- В противном случае производится новое разбиение окна.
Шаги 1–4 рассматривают ситуацию пересечения окна только с одним многоугольником. Они используются для сокращения числа подразбиений. Шаг 5 решает задачу удаления невидимых поверхностей. Многоугольник, находящийся ближе всех к точке наблюдения, экранирует все остальные.
Для реализации алгоритма необходимы функции, определяющие взаимное расположение окна и многоугольника, которые достаточно легко реализуются в случае прямоугольных окон и выпуклых многоугольников. Для определения, является ли многоугольник охватывающим, внешним или внутренним, можно воспользоваться, например, погружением многоугольника в прямоугольную оболочку. Для определения наличия пересечений можно использовать опорные прямые (так же, как использовались плоскости в алгоритме Робертса). Если же многоугольник невыпуклый, то задача усложняется. Методы решения такого рода задач будут рассмотрены в главе, относящейся к геометрическому поиску.
Следует заметить, что существуют различные реализации алгоритма Варнока. Были предложены варианты оптимизации, использующие предварительную сортировку многоугольников по глубине, т. е. по расстоянию от точки наблюдения, и другие.
Алгоритм Вейлера-Азертона
Вейлер и Азертон попытались оптимизировать алгоритм Варнока в отношении числа выполняемых разбиений, перейдя от прямоугольных разбиений к разбиениям вдоль границ многоугольников (1977). Для этого они использовали ими же разработанный алгоритм отсечения многоугольников. Алгоритм работает в объектном пространстве, и результатом его работы являются многоугольники. В самом общем виде он состоит из четырех шагов.
- Предварительная сортировка по глубине.
- Отсечение по границе ближайшего к точке наблюдения многоугольника, называемое сортировкой многоугольников на плоскости.
- Удаление многоугольников, экранируемых более близкими к точке наблюдения многоугольниками.
- Если требуется, то рекурсивное разбиение и новая сортировка.
В процессе предварительной сортировки создается список приблизительных приоритетов, причем близость многоугольника к точке наблюдения определяется расстоянием до ближайшей к ней вершины. Затем выполняется отсечение по самому первому из многоугольников. Отсечению подвергаются все многоугольники из списка, причем эта операция выполняется над проекциями многоугольников на картинную плоскость. При этом создаются списки внешних и внутренних фигур. Все попавшие в список внешних не экранируются отсекающим многоугольником. Затем рассматривается список внутренних многоугольников и выполняется сортировка по расстоянию до отсекающего многоугольника. Если все вершины некоторого многоугольника оказываются дальше от наблюдателя, чем самая удаленная из вершин экранирующего, то они невидимы, и тогда они удаляются. После этого работа алгоритма продолжается с внешним списком.
Если какая-то из вершин внутреннего многоугольника оказывается ближе к наблюдателю, чем ближайшая из вершин экранирующего многоугольника, то такой многоугольник является частично видимым. В этом случае предварительный список приоритетов некорректен, и тогда в качестве нового отсекающего многоугольника выбирается именно этот "нарушитель порядка". При этом используется именно исходный многоугольник, а не тот, что получился в результате первого отсечения. Такой подход позволяет минимизировать число разбиений.
Этот алгоритм в дальнейшем был обобщен Кэтмулом (1974) для изображения гладких бикубических поверхностей. Его подход заключался в том, что разбиению подвергалась поверхность. Коротко этот алгоритм можно описать так:
- Рекурсивно разбивается поверхность до тех пор, пока проекция элемента на плоскость изображения не будет покрывать не больше одного пикселя.
- Определить атрибуты поверхности в этом пикселе и изобразить его.
Эффективность такого метода, как и алгоритм Варнока, зависит от эффективности разбиений. В дальнейшем этот алгоритм был распространен на сплайновые поверхности.
Метод Z-буфера
Это один из простейших алгоритмов удаления невидимых поверхностей.
Впервые он был предложен Кэтмулом в 1975 г. Работает этот алгоритм в
пространстве изображения. Идея Z-буфера является простым обобщением
идеи о буфере кадра. Буфер кадра используется для запоминания
атрибутов каждого пикселя в пространстве изображения, а Z-буфер
предназначен для запоминания глубины (расстояния от картинной
плоскости) каждого видимого пикселя в пространстве изображения.
Поскольку достаточно распространенным является использование
координатной плоскости  в качестве картинной плоскости, то глубина
равна координате
в качестве картинной плоскости, то глубина
равна координате  точки, отсюда и название буфера. В процессе работы
значение глубины каждого нового пикселя, который нужно занести в буфер
кадра, сравнивается с глубиной того пикселя, который уже занесен в Z-буфер.
Если это сравнение показывает, что новый пиксель расположен
впереди пикселя, находящегося в буфере кадра, то новый пиксель
заносится в этот буфер и, кроме того, производится корректировка Z-буфера
новым значением глубины. Если же сравнение дает противоположный
результат, то никаких действий не производится. По сути, алгоритм
является поиском по
точки, отсюда и название буфера. В процессе работы
значение глубины каждого нового пикселя, который нужно занести в буфер
кадра, сравнивается с глубиной того пикселя, который уже занесен в Z-буфер.
Если это сравнение показывает, что новый пиксель расположен
впереди пикселя, находящегося в буфере кадра, то новый пиксель
заносится в этот буфер и, кроме того, производится корректировка Z-буфера
новым значением глубины. Если же сравнение дает противоположный
результат, то никаких действий не производится. По сути, алгоритм
является поиском по  и
и  наибольшего значения функции
наибольшего значения функции  .
.
Главное преимущество алгоритма - его простота. Кроме того, этот алгоритм решает задачу об удалении невидимых поверхностей и делает тривиальной визуализацию пересечений сложных поверхностей. Сцены могут быть любой сложности. Поскольку габариты пространства изображения фиксированы, оценка вычислительной трудоемкости алгоритма не более чем линейна. Поскольку элементы сцены или картинки можно заносить в буфер кадра или в Z-буфер в произвольном порядке, их не нужно предварительно сортировать по приоритету глубины. Поэтому экономится вычислительное время, затрачиваемое на сортировку по глубине.
Основной недостаток алгоритма - большой объем требуемой памяти. В последнее время в связи с быстрым ростом возможностей вычислительной техники этот недостаток становится менее лимитирующим. Но в то время, когда алгоритм еще только появился, приходилось изобретать способы создания буфера как можно большего объема при имеющемся ресурсе памяти.
Например, можно разбивать пространство изображения на 4, 16 или больше прямоугольников или полос. В предельном варианте можно использовать буфер размером в одну строку развертки. Для последнего случая был разработан алгоритм построчного сканирования. Поскольку каждый элемент сцены обрабатывается много раз, то сегментирование Z-буфера, вообще говоря, приводит к увеличению времени, необходимого для обработки сцены.
Другой недостаток алгоритма состоит в трудоемкости реализации эффектов, связанных с полупрозрачностью, и ряда других специальных задач, повышающих реалистичность изображения. Поскольку алгоритм заносит пиксели в буфер кадра в произвольном порядке, то довольно сложно получить информацию, которая необходима для методов, основывающихся на предварительном анализе сцены.
В целом алгоритм выглядит так:
- Заполнить буфер кадра фоновым значением цвета.
- Заполнить Z -буфер минимальным значением z (глубины) .
- Преобразовать изображаемые объекты в растровую форму в произвольном порядке.
- Для каждого объекта:
4.1. Для каждого пикселя  образа вычислить его глубину
образа вычислить его глубину 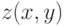 .
.
4.2. Сравнить глубину 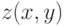 со значением глубины, хранящимся в Z-буфере в этой же позиции.
со значением глубины, хранящимся в Z-буфере в этой же позиции.
4.3. Если  , то занести атрибуты пикселя в буфер кадра и заменить
, то занести атрибуты пикселя в буфер кадра и заменить 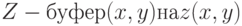 . В противном случае никаких действий не производить.
. В противном случае никаких действий не производить.
Алгоритм, использующий Z-буфер, можно также применять для построения сечений поверхностей. Изменится только оператор сравнения:
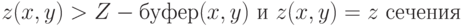
 - глубина искомого сечения.
- глубина искомого сечения.