Линейные коды и способы модуляции

Фазовая манипуляция

Фазовая манипуляция передает информацию путем воздействия цифрового сигнала на фазу частотного сигнала. Общая формула, отображающая фазовую манипуляцию:

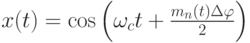
где 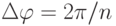тогда

Значение — число уровней исходного сигнала. Если принять, что уровни сигналов подчиняются закону , то 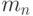принимает все значения, перечисленные приведенной ниже формулой:

.

Например, при 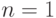(одноуровневый сигнал со значением 0 или 1)

.

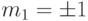Тогда амплитуда сигнала (определяется в точке ) будет равна

при значении сигнала 1

;

при значении сигнала 0

.

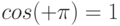Например, в простейшем случае передачи отдельных бит (рис.9.10) при переходе от 0 к 1 фаза меняется на 180 градусов ( ).

В ситуации, показанной на рис. 9.4, значению 1 соответствует положительный период в начале цикла, а значению 0 — отрицательный.

Рис. 9.4. Фазовая манипуляция 2–ФМ (серым цветом отмечен момент анализа фазы)

При 4-фазовой манипуляции ( ) в момент времени 0:

сигнал первого уровня 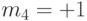амплитуда ;

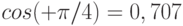сигнал второго уровня 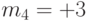амплитуда ;

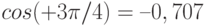сигнал третьего уровня 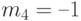амплитуда ;

сигнал четвертого уровня 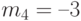амплитуда .

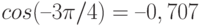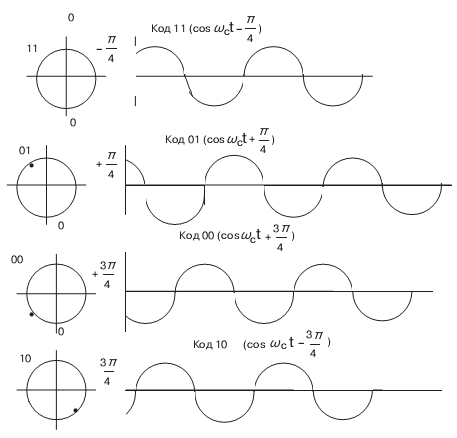
На рис. 9.5 показан пример диаграмм для фазового сдвига при различных многоуровневых комбинациях.

Фаза определяется с помощью измерения значения косинусоидального сигнала в начале периода.

Рис. 9.5. Фазовые манипуляции 4-ФМ

Сбоку на рисунках показаны круговые диаграммы синусоидального сигнала (на рис. 9.5 сигнал показывает значения косинуса и потому сдвинут на 90 градусов). Изменение значения синусоидального сигнала сопоставляется со значением, изображаемым на круге. При этом при течении времени воображаемый вектор (радиус, помещенный в центр круга) вращается против часовой стрелки. Точка на круге показывает значение синусоидального сигнала в данный момент времени. Соответственно, на диаграмме нижняя точка на круге соответствует минимальному отрицательному значению амплитуды и сопоставляется с дискретной единицей (1), а высшая точка соответствует максимальному значению и отождествляется с дискретным нулем (0). Для диаграммы, показывающей четырехкратный сдвиг фазы, намечены 4 точки.

Ниже на рис. 9.6 показан сигнал после фазовой манипуляции последовательности 00100111.

Исходная последовательность цифрового сигнала аналогична многоуровневому коду, показанному на рис. 9.4.

Заметим, что при способе 4-ФМ передача данных ускоряется в 2 раза по сравнению с исходным цифровым потоком. Иногда для выравнивания скоростей применяют прием, при котором моменты анализа фазы при системе 4-ФМ в два раза реже, чем при 2-ФМ, что обеспечивает одинаковую скорость передачи данных.

В отличие от амплитудной модуляции, фазовая менее подвержена воздействию на уровень передачи (влияния на амплитуду) и частоту. Она наиболее приспособлена к передаче многоуровневых сигналов, которые, как мы знаем из предыдущего раздела, позволяют повысить скорость передачи информации, не повышая линейную скорость в канале. Однако на нее очень влияют индуктивные и емкостные параметры кабеля. Например, пупиновские катушки, упомянутые в "Линейные устройства. Факторы, ухудшающие передачу" , улучшая параметры обычного сигнала, вносят искусственную индуктивность, которая в свою очередь влияет на сигналы, уплотненные с помощью фазовой модуляции.

Рис. 9.6. Пример сигнала фазовой манипуляции последовательностью 00100111

Возможно построение фазовой манипуляции при большем числе уровней, например 8-ФМ, но это построение заложено в разделе упражнений.

Рассмотрим теперь принципы реализации этого способа. Общее выражение фазовой модуляции определяется формулой

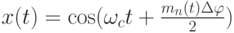
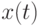— это форма модулированного сигнала,

где — 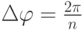, 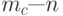уровневый сигнал в виде симметричных импульсов постоянного тока без возвращения к нулю, а значения уровней равны .

Квадратурное представление сигнала

Рассмотрим тригонометрическое тождество

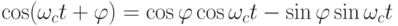
Полученная формула позволяет свести процесс фазовой модуляции к комбинации амплитудной модуляции двух последовательностей сигналов с нулевым фазовым сдвигом.

Представление синусоидального колебания как линейной комбинации синусоидального и косинусоидального колебаний с нулевой начальной фазой называется квадратурным представлением.

Функции и для каждого такта передачи сигнала являются постоянными, т.е. играют роль коэффициентов, принимающих значения в соответствии с уровнем сигнала. Функции и 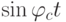играют роль несущих частот, сдвинутых на 90 градусов (находятся в "квадратуре"). При сложении двух амплитудно-модулированных функций получается одна функция с фазовой модуляцией. Косинусоидальные сигналы обычно называют синфазными сигналами или "I-сигналами", синусоидальные — сдвинутыми сигналами или "Q-сигналами".

Структурная схема ФМ-модулятора, построенного по этому принципу, показана на рис. 9.7.