|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Подписные листы (LISTSERV) и поисковые системы
В случаях, когда поисковая система выдает заказчику большой список документов, отвечающих критериям его запроса, бывает важно, чтобы они были упорядочены согласно их степени соответствия (наличие ключевых слов в заголовке, большая частота использования ключевых слов в тексте документа и т.д.). Но простые критерии здесь не всегда срабатывают: так, объемный документ имеет больше шансов попасть в список результата поиска, поскольку в нем много слов и с большой вероятностью там встречается ключевое слово. По этому критерию Британская энциклопедия должна попасть в результирующий список любого запроса. Для компенсации искажений, вносимых длиной документов, используется нормализация весов индексных терминов.
Нормализация представляет собой способ уменьшения абсолютного значения веса индексных терминов, обнаруженных в документе. Одним из наиболее распространенных методов, решающих данную проблему, является косинусная нормализация. При использовании этого метода нормализации вес каждого индексного термина делится на Евклидову длину вектора оцениваемого документа. Евклидова длина вектора определяется формулой:
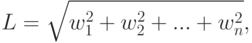
– вес i -того термина в документе, tf (term frequency) — частота, с которой встречается данный индексный термин; IDF (Inverted Document Frequency) — величина, обратная частоте, с которой данный термин встречается во всей совокупности документов. Окончательная формула для вычисления веса термина ( w ) в документе с учетом косинусного фактора нормализации представляется формулой:
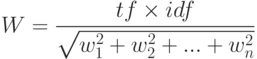
Термины, которые отсутствуют в тексте документа, имеют нулевой вес. В списке, возвращаемом на запрос, документы перечисляются в порядке уменьшения данного численного значения.
В работах Букштейна, Свенсона и Хартера было показано, что распределение функциональных слов, в отличие от специфических слов, с хорошей точностью описывается распределением Пуассона. То есть, если отыскивается распределение функционального слова w в некотором множестве документов, тогда вероятность f(n) того, что слово w будет встречено в тексте n раз представляется функцией:
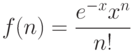
– распределение Пуассона. Значение параметра x варьируется от слова к слову и для конкретного слова должно быть пропорционально длине текста. Слова, распределенные в совокупности документов согласно Пуассону, полезной информации не несут.
Для представления документов используется векторная модель, в которой любой документ характеризуется бинарным вектором x = x1,x2,...,xn, где значения xi = 0 или 1, в зависимости от того, присутствует в тексте i -ый индексный термин или нет. Рассматриваются два взаимно исключающих события:
w1 — документ удовлетворяет запросу; w2 — документ не удовлетворяет запросу
Для определения того, какие документы удовлетворяют запросу, а какие нет, необходимо вычислить условные вероятности P(w1|x) и P(w2|x).
Непосредственно получить значения этих вероятностей нельзя, поэтому необходимо найти другой альтернативный подход для их определения с помощью известных нам величин. По формуле Байеса для дискретного распределения условных вероятностей:
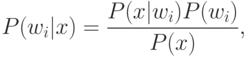
В приведенной формуле P(w1) — первоначальная вероятность соответствия ( i = 1 ) или несоответствия ( i = 2 ) запросу, величина P(x|wi) пропорциональна вероятности соответствия или несоответствия запросу для данного x ; в недискретном случае она представляет собой функцию плотности распределения и обозначается как P(x|wi).
Окончательно:

что представляет собой вероятность получения документа x в ответ на запрос, при условии, что он будет ему соответствовать. P(x) выступает в качестве нормализующего фактора (т.е. с его помощью достигается выполнение условия P(w1|x)+P(w2|x)=1 ).
Для определения релевантности документа используется вполне очевидное правило:
Если P(w1|x)>P(w2|x), то документ удовлетворяет запросу [1].
В противном случае считается, что документ не удовлетворяет запросу. При равенстве значений вероятности решение о релевантности документа принимается произвольно.
Правило [1] основано на том, что при его использовании просто минимизируется средняя вероятность ошибки принятия нерелевантного документа за релевантный и наоборот. То есть, для любого документа x вероятность ошибки P(error|x) равна:
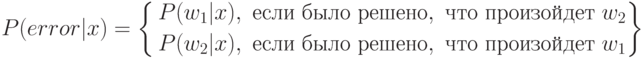
Таким образом, для минимизации средней вероятности ошибки необходимо минимизировать функцию 
Не углубляясь в теорию вероятностного нахождения релевантных документов, укажем еще одно правило, которое можно использовать вместо [1]:
(l21-l11)P(x|w1)P(w1)>(l12-l22)P(x|w2)P(w2)Листинг 2.
В формуле [2] коэффициенты lij стоимостной функции определяют потери, вносимые при ожидании события wi, когда на самом деле произошло событие wj.
Для практической реализации вероятностного поиска вводится упрощающее предположение относительно P(x|wi). Принимается, что значения xi вектора x являются статистически независимыми. Данное утверждение математически представляется в виде:
P(x|wi)=P(x1|wi)P(x2|wi)...P(xn|wi).
Определим переменные: pi=Pr ob(xi=1/w1) и qi=Pr ob(xi=1/w2), представляющие собой вероятность того, что в документе присутствует i -ый индексный термин при условии, что документ является релевантным (нерелевантным). Соответствующая вероятность для отсутствия индексных терминов имеет вид: 1-pi=Pr ob(xi=0/wi)
Вероятностные функции, используемые для подстановки в правило [1], имеют вид:
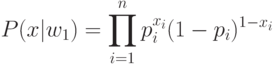
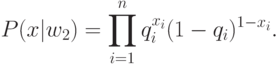
Подставляя значения P(x|wi) в [2] и логарифмируя, получаем:
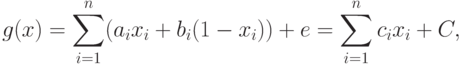
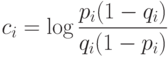
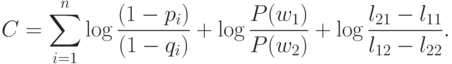
Функция G(x) представляет собой не что иное, как весовую функцию, в которой коэффициенты Сi есть веса присутствующих в документе индексных терминов. Константа С одинакова для всех документов x, но, конечно, различна для разных запросов и может рассматриваться в качестве порогового значения для поисковой функции. Единственными параметрами, которые могут меняться для данного запроса, являются параметры стоимостной функции, вариации которых позволяют получать в ответе большее или меньшее число документов.
