|
Подскажите, пожалуйста, планируете ли вы возобновление программ высшего образования? Если да, есть ли какие-то примерные сроки? Спасибо! |
Статистическое моделирование
3.2. Общая характеристика метода имитационного моделирования
Имитационное моделирование представляет собой процесс построения и испытания некоторого моделирующего алгоритма, имитирующего поведение и взаимодействие исследуемой системы с учетом случайных входных воздействий и внешней среды.
Имитационная модель обладает самым главным свойством моделей вообще - она может быть объектом эксперимента, причем эксперимент проводится с моделью, представленной в виде компьютерной программы.
Имитационная модель отображает стохастический процесс смены дискретных состояний системы. При реализации модели на компьютере производится накопление статистических данных по показателям модели, которые являются предметом исследований. По окончании моделирования накопленная статистика обрабатывается, и результаты моделирования получаются в виде выборочных распределений исследуемых величин. Таким образом, математическая статистика и теория вероятностей являются математическими основами имитационного моделирования.
Имитационные модели могут быть реализованы средствами универсальных языков программирования (Паскаль, Си, Фортран и др.). Они предоставляют практически неограниченные возможности в разработке и отладке программ моделей. Однако, модель в виде программы на универсальном языке программирования часто непонятна исследователю. Ведь совершенно необязательно исследователь, специалист в конкретной предметной области должен знать тонкости программирования на каком-либо языке. Поэтому были созданы специализированные языки моделирования, которые существенно упрощают создание моделей и обработку результатов моделирования (Симпас, Симула, Арена, семейство языков GPSS и др.). Одна из наиболее распространенных систем моделирования GPSS World рассматривается в настоящем курсе.
Имитационная модель может представить объект практически любой сложности. Ограничениями могут служить лишь недостаточная квалификация исполнителя, а также требование адекватности модели и достижения очень большой точности результата. А это связано с получением статистических выборок большого объема, что ведет к необходимости получения большого числа реализаций модели и, следовательно, высокопроизводительных компьютеров.
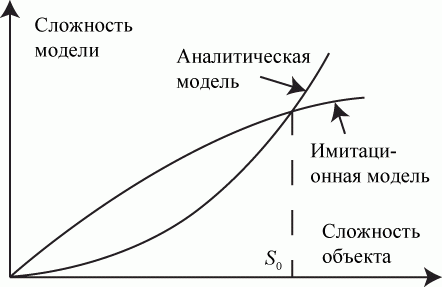
Если сложность аналитической модели с усложнением моделируемого объекта возрастает с ускорением, как показано на рис. 3.6, то сложность имитационной модели, начиная с некоторого уровня  растет незначительно.
растет незначительно.
К достоинствам имитационных моделей можно также отнести:
- простота алгоритма;
- малая связность алгоритма;
- устойчивость к случайным сбоям компьютера, так как при большом числе реализаций (прогонов) модели сбой в одной из них исказит статистику несущественно.
Недостатком имитационного моделирования является то, что решение, результат является численным, частным, справедливым только для конкретных значений исходных данных. Чтобы получить функциональные зависимости между параметрами исследуемого процесса (системы) потребуется сделать очень большое количество вариантов решений. Аналитическая же модель дает, как правило, функциональные зависимости. Если сложность задачи, требуемая точность решения, возможности математики и способности исследователя позволяют построить математическую аналитическую модель, то следует использовать ее.
Метод имитационного моделирования стал развиваться с появлением цифровых вычислительных машин, большой производительностью и памятью. Отметим, что именно необходимость широкого применения статистического моделирования является одним из существенных стимулов создания высокопроизводительных компьютеров.
Одной из основных целей имитационного моделирования является определение показателей эффективности различных операций. Показатели эффективности могут выступать в виде оценок характеристик случайных величин или процессов или вероятностей исхода операций. В первом случае - это время, расход ресурсов, численности противоборствующих сторон, расстояния и т. п. Во втором случае показатель эффективности выступает в качестве вероятности, например, достижения цели операции в заданный срок, исправного состояния техники и т. д.
3.3. Статистическое моделирование при решении детерминированных задач
Метод статистических испытаний может быть использован как численный метод решения математических задач. Именно в таком качестве он был применен в США в 1944 г. Джоном фон Нейманом при расчетах по созданию ядерного реактора.
Применение метода рассмотрим на примере вычисления некоторого интеграла.
Пример 3.4. Пусть 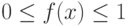 ,
, 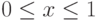 . Полагаем, что функция
. Полагаем, что функция 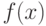 такова, что интеграл относится к "неберущимся".
такова, что интеграл относится к "неберущимся".
Требуется вычислить 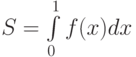 .
.
Решение
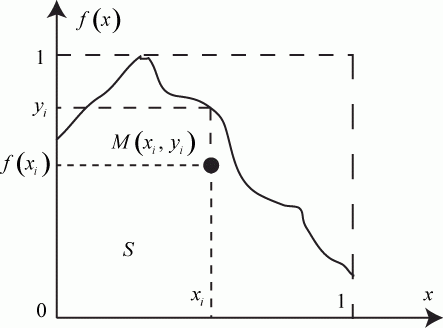
Представим функцию в координатах 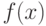 и
и 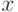 как показано на рис. 3.7. Как известно, численное значение интеграла данного вида равно площади
как показано на рис. 3.7. Как известно, численное значение интеграла данного вида равно площади  . Площадь
. Площадь 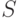 состоит из множества элементарных площадок - точек. Количество точек в этой площади и будет численным значением искомого интеграла.
состоит из множества элементарных площадок - точек. Количество точек в этой площади и будет численным значением искомого интеграла.
Имитируем координаты каждой точки значениями 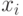 и
и  , принадлежащими равномерному распределению на участке
, принадлежащими равномерному распределению на участке ![[0, 1]](/sites/default/files/tex_cache/264884439b70ab09a86bc848421c6de6.png) :
:
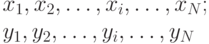
Рассмотрим пару чисел 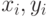 . Вычислим
. Вычислим 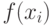 и сравним с
и сравним с  . Если
. Если 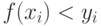 , то это означает, что точка
, то это означает, что точка 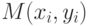 принадлежит площади
принадлежит площади  . Если
. Если 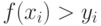 , то это означает, что точка
, то это означает, что точка 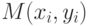 не принадлежит площади
не принадлежит площади 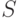 .
.
Введем:
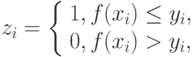
Число точек, попавших в границы 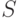 равно
равно 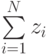 , где
, где  - общее число точек, попавших в единичную площадь существования функции и аргумента. Отсюда следует:
- общее число точек, попавших в единичную площадь существования функции и аргумента. Отсюда следует:
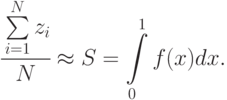
Чем больше будет элементарных площадей - точек, тем точнее будет вычислен интеграл. Приведенное решение примера справедливо для единичных областей существования функции и аргумента. Однако это несущественно, так как произвольные границы существования 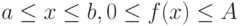 заменой переменных можно свести к единичным границам.
заменой переменных можно свести к единичным границам.
Известны статистические алгоритмы численного решения многократных интегралов.
Пример 3.5. Найти оценку  интеграла
интеграла 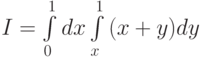 .
.
Решение
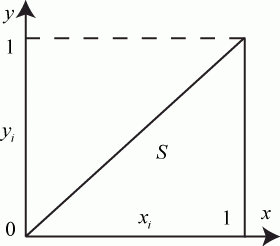
Область интегрирования ограничена линиями 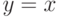 ,
, 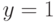 ,
, 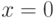 , т. е. принадлежит единичному квадрату (рис. 3.8).
, т. е. принадлежит единичному квадрату (рис. 3.8).
Площадь области интегрирования (прямоугольного треугольника) 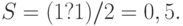 Используем формулу
Используем формулу
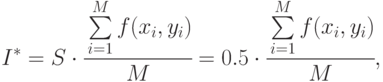
в которой 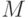 - число случайных точек
- число случайных точек 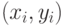 , принадлежащих области интегрирования. У этих точек
, принадлежащих области интегрирования. У этих точек  . Если данное условие выполняется, то вычисляется
. Если данное условие выполняется, то вычисляется
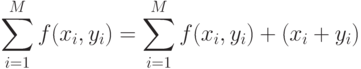
а число случайных точек 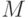 увеличивается на
увеличивается на  :
: 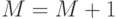 .
.
Результаты моделирования приведены в табл. 3.2.
Из данных табл. 3.2 (верхние пять строк) видно, что с увеличением числа реализаций  ошибка
ошибка 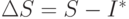 в определении оценки интеграла
в определении оценки интеграла 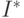 уменьшается и при
уменьшается и при 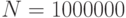 становится равной нулю.
становится равной нулю.
 |
10 | 1000 | 10000 | 100000 | 1000000 |
 |
5 | 500 | 5038 | 49658 | 500364 |
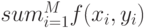 |
4,773 | 487,695 | 5006,152 | 49533,242 | 500191,650 |
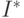 |
0,477 | 0,488 | 0,497 | 0,499 | 0,500 |
 |
0,023 | 0,012 | 0,003 | 0,001 | 0 |
 |
6 | 503 | 4935 | 49833 | |
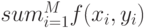 |
5,025 | 494,593 | 4917,236 | 49802,019 | |
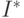 |
0,419 | 0,492 | 0,498 | 0,500 | |
 |
0,081 | 0,008 | 0,002 | 0 |
В четырех нижних строках табл. 3.2 приведены результаты моделирования с другими начальными числами генераторов равномерно распределенных случайных чисел. Как видно, ошибка в оценке интеграла равна нулю уже при  реализаций модели.
реализаций модели.
В заключение отметим, что имитационное (статистическое) моделирование целесообразно применять в случаях:
- когда нет законченной математической постановки задачи;
- когда нет аналитических методов решения сформулированной задачи;
- когда аналитические методы есть, но они не удовлетворяют требованиям точности и достоверности;
- когда аналитические методы есть, но их вычислительные процедуры сложны даже для компьютера;
- когда реализация известных процедур сталкивается с недостаточной математической подготовкой исследователя;
- когда исследователю нужно знать не только оценки искомых характеристик, но и динамику всего случайного процесса.