НОУ ИНТУИТ | Компьютерное моделирование. Лекция 6: Обработка результатов имитационного эксперимента

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 16.11.2010 | Уровень: специалист | Доступ: свободно

|

Вам нравится? Нравится 50 студентам

| Поделиться |

Поддержать программу

5.10. Обработка результатов эксперимента на основе регрессии

Часто целью исследования является определение функциональной связи между факторами и откликом (реакцией модели) по данным, полученным при экспериментах с моделью объекта или непосредственно с объектом. Такая цель достигается регрессионным анализом значений факторов и отклика .

Под регрессией в теории вероятностей и математической статистике понимают зависимость среднего значения какой-либо величины от некоторой другой (других) величины. Регрессионный анализ - это совокупность методов построения и исследования регрессионной зависимости между величинами (в нашем случае между факторами и откликом) по статистическим данным. Статистические данные накапливаются при проведении эксперимента.

Формальная схема эксперимента выглядит так (рис. 5.6).

Рис. 5.6. Формальная схема эксперимента

Прямоугольник представляет исследуемый объект или его математическую модель. Обозначения на рис. 5.6:

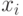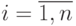$x_{i}$ - значения факторов, $i = \overline{1, n}$ ;

$\xi$ - случайный фактор, помеха. Будем считать, что эта случайная величина имеет нормальное распределение с матожиданием $M[\xi] = 0$ . Влияние помехи на отклик аддитивное, то есть ее случайные значения прибавляются к значениям отклика;

f(x) - искомая функциональная зависимость между факторами и откликом.

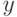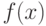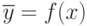Отклик - величина случайная. f(x) представляет собой среднее значение отклика (так как $M[\xi] = 0$ ): $\overline{y} = f(x)$ .

Исследуемый объект представляется как "черный ящик", никаких предположений о виде функции f(x) нет. Поэтому представим ее в виде аппроксимирующего полинома:

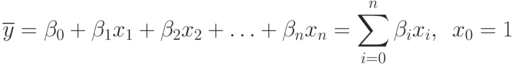
$\overline{y}=\beta_0+\beta_1 x_1+\beta_2 x_2 + \ldots + \beta_n x_n = \sum\limits_{i=0}^{n}{\beta_ix_i},\,\,\, x_0=1$

Этот полином получил название уравнения регрессии, а коэффициенты 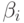$\beta_{i}$ - коэффициенты регрессии. От точности подбора коэффициентов регрессии зависит точность представления f(x) .

Коэффициенты 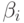$\beta_{i}$ определяются путем обработки полученных в ходе эксперимента варьируемых значений факторов и откликов.

Однако из-за ограниченного числа наблюдений точные значения $\beta _{i}$ получить нельзя, будут найдены их оценки $b_{i}$ :

$\overline{\beta _{i}}=b_{i}.$

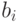Поэтому уравнение регрессии принимает вид:

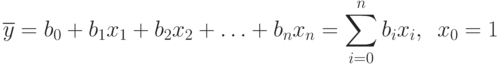
$\overline{y}=b_0+b_1 x_1+b_2 x_2 + \ldots + b_n x_n = \sum\limits_{i=0}^{n}{b_ix_i},\,\,\, x_0=1$

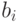Вообще-то метку над $\overline{y}$ теперь надо бы изменить, так как вместо $\beta _{i}$ в уравнении теперь стоят $b_{i}$ , но мы этого делать не будем, чтобы не загромождать изложение новыми значками.

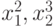В уравнении регрессии могут участвовать и так называемые "совместные эффекты" ( $x_{1}x_{2},x_{1}x_{2}x_{3}$ и т. п.) или степени значений факторов ( $x_{1}^{2},x_{2}^{3}$ и т. п.). Совместные эффекты и степени факторов можно обозначать обобщенным фактором. Например, уравнение регрессии

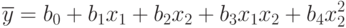
$\overline{y}=b_0+b_1x_1+b_2x_2+b_3x_1x_2+b_4x_2^2$

можно представить так:

$\overline{y}=b_0+b_1x_1+b_2x_2+b_3x_3+b_4x_4,\,\,\,x_3=x_1x_2,\,\,\,x_4=x_2^2$

Итак, для определения выражения f (x) надо:

выбрать степень аппроксимирующего полинома - уравнения регрессии;
определить коэффициенты регрессии.

Выбор уравнения регрессии обычно начинают с линейной модели. Например, для двухфакторного эксперимента ее вид:

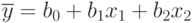
$\overline{y}=b_0+b_1x_1+b_2x_2$

Если окажется, что такая аппроксимация дает неприемлемые отклонения при сравнении с экспериментальными точками отклика y , то модель усложняется, например, так:

$\overline{y}=b_0+b_1x_1+b_2x_2+b_3x_1x_2$ или

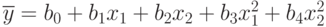$\overline{y}=b_0+b_1x_1+b_2x_2+b_3x_1^2+b_4x_2^2$ и т.д.

Коэффициенты регрессии 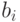$b_{i}$ для выбранного уравнения определяются из условия минимума суммы квадратов ошибок, вычисленных по все экспериментальным точкам. Это делается так. Введем обозначения:

$x_{il}$ - значение -го фактора в наблюдении номер ;

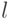$y_{l}$ - значение отклика в 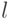-м наблюдении;

$\overline{y}_{l}$ - значение отклика, вычисленное по принятому уравнению регрессии и данным $x_{il}$ .

Очевидно, сумма квадратов ошибок между экспериментальными значениями $y_{l}$ и вычисленными по уравнению регрессии $y_{l }$ для всех наблюдений равна:

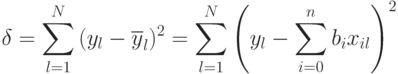
$\delta=\sum\limits_{l=1}^{N}{(y_l-\overline{y}_l)^2}=\sum\limits_{l=1}^{N}{\left ( y_l - \sum\limits_{i=0}^{n}{b_ix_{il}} \right )^2}$

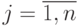Для определения минимума ошибки ?возьмем частные производные от $\delta$ по всем неизвестным коэффициентам регрессии b_j , $j = \overline{1, n}$ и приравняем их нулю:

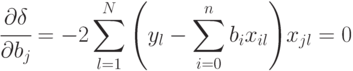
$\cfrac{\partial\delta}{ \partial b_j} =-2\sum\limits_{l=1}^{N}{\left ( y_l - \sum\limits_{i=0}^{n}{b_ix_{il}} \right )}x_{jl}=0$

Нетрудно убедиться, что это условие минимума, а не максимума. Очевидно:

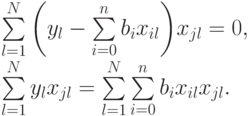
$\sum\limits_{l=1}^{N}{\left ( y_l - \sum\limits_{i=0}^{n}{b_ix_{il}} \right )}x_{jl}=0,\\ \sum\limits_{l=1}^{N}{y_l x_{jl}}=\sum\limits_{l=1}^{N}{\sum\limits_{i=0}^{n}{b_i x_{il}x_{jl}}}.$

Для лучшей наглядности выделим неизвестные коэффициенты регрессии и получим:

$\sum\limits_{l=1}^{N}{y_l x_{jl}}= \sum\limits_{l=1}^{N}{b_i}\sum\limits_{i=0}^{n}{x_{il}x_{jl}}$

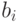Выражение (5.3) представляет собой систему из n + 1 уравнений для нахождения n +1 неизвестных коэффициентов регрессии $b_{i}$ , которые окончательно определят выбранное уравнение регрессии.

Нахождение коэффициентов регрессии справедливо при следующих допущениях:

Случайный фактор 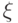$\xi$ имеет нормальное распределение с матожиданием $М[ \xi ] = 0$ .
Результаты наблюдений $y_{l}$ - независимые нормально распределенные случайные величины. Если это не соблюдается, то следует измерять другой отклик, удовлетворяющий этому условию, но функционально связанный с исследуемым откликом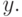
Точность наблюдений (количество реализаций модели) не меняется от наблюдения к наблюдению.
Точность наблюдения 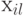$х_{il}$ должна быть выше точности $y_{l}$ .

Пример 5.8. На модели объекта проведен однофакторный эксперимент из пяти наблюдений, результаты которого сведены в таблицу (табл. 5.10).

Найти функциональную связь фактора с откликом 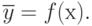$\overline{y} = f(х).$

Таблица 5.10. Результаты эксперимента
Фактор и отклики	Наблюдение		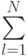			$\sum\limits_{l=1}^N$
Фактор и отклики	1	2	3	4	5	$\sum\limits_{l=1}^N$
$x_{1l}$	0	0,5	1,0	1,5	2,0	5
$y_{l}$	7,0	4,8	2,8	1,4	0	16
$y_lx_{1l}$	0	2,4	2,8	2,1	0	7,3

Решение

Примем, что кроме управляемого фактора 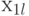$х_{1l}$ при проведении эксперимента на объект воздействует случайный фактор, распределенный по нормальному закону с математическим ожиданием $М[\xi] = 0$ . Также предположим, что эта связь - линейная, следовательно, уравнение регрессии нужно определять в виде:

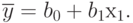
$\overline{y} = b_{0} + b_{1}х_{1}.$

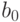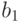Неизвестных коэффициентов два: $b_{0}$ и $b _{1}$ . Запишем (5.3) в виде двух уравнений для $j = 0,\, j = 1$ и в каждом из них разложим суммы по индексу :

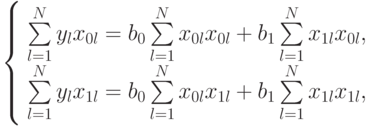
$\left \{ \begin{array}{l} \sum\limits_{l=1}^{N}{y_lx_{0l}} = b_0\sum\limits_{l=1}^{N}{x_{0l}x_{0l}} + b_1\sum\limits_{l=1}^{N}{x_{1l}x_{0l}},\\ \sum\limits_{l=1}^{N}{y_lx_{1l}} = b_0\sum\limits_{l=1}^{N}{x_{0l}x_{1l}} + b_1\sum\limits_{l=1}^{N}{x_{1l}x_{1l}}, \end{array}$

Так как $х_{0l} = 1$ , получим:

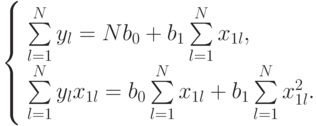
$\left \{ \begin{array}{l} \sum\limits_{l=1}^{N}{y_l} = Nb_0 + b_1\sum\limits_{l=1}^{N}{x_{1l}},\\ \sum\limits_{l=1}^{N}{y_lx_{1l}} = b_0\sum\limits_{l=1}^{N}{x_{1l}} + b_1\sum\limits_{l=1}^{N}{x_{1l}^2}. \end{array}$

Подставим данные эксперимента из табл. 5.10 в систему (5.4):

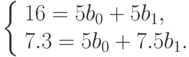
$\left \{ \begin{array}{l} 16=5b_0+5b_1,\\ 7.3=5b_0+7.5b_1. \end{array}$

Решим систему из двух уравнений и получим: 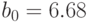$b_{0} =6.68$ , $b _{1} =-3.48$ .

Следовательно, искомое уравнение регрессии:

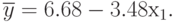
$\overline{y} = 6.68-3.48х_{1}.$

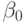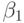Доверительные границы для истинных значений $\beta _{0}$ и $\beta _{1}$ примера 5.8 определяются как обычно:

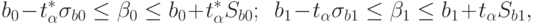
$b _{0} -t _{\alpha } ^{*} \sigma _{b0} \le \beta _{0} \le b _{0} +t _{\alpha }^{*} S_{b0} ;\,\,\, b _{1} -t_{\alpha } \sigma_{b1} \le\beta _{1}\le b _{1} +t_{\alpha } S_{b1},$

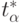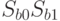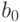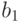где $t _{\alpha }^*$ - аргумент распределения Стьюдента; $S_{b0} S_{b1}$ - среднеквадратические отклонения величин $b_{0}$ и $b _{1}$ соответственно.

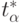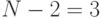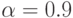Значения $t _{\alpha }^*$ определяются из таблицы распределения Стьюдента для N-2 = 3 степеней свободы и задаваемом уровне достоверности $\alpha$ . Пусть $\alpha = 0.9$ , тогда $t^*_{\alpha } \approx 2.35$ .

Значения 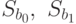$S_{b_0},\,\, S_{b_1}$ находятся по формулам:

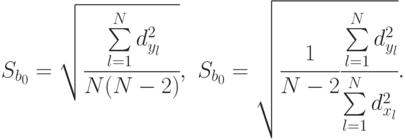
$S_{b_0}=\sqrt{\cfrac{\sum\limits_{l=1}^{N}{d_{y_l}^2}}{N(N-2)}},\,\, S_{b_0}=\sqrt{\cfrac {1}{N-2}\cfrac{\sum\limits_{l=1}^{N}{d_{y_l}^2}}{\sum\limits_{l=1}^{N}{d_{x_l}^2}}}.$

Данные для вычисления 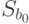$S_{b_0}$ , $S_{b_1}$ представлены в табл. 5.11.

Таблица 5.11. Данные для вычисления S_b0, S_b1
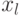
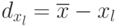
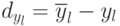
	$x_{l}$	$d_{x_l}=\overline{x}-x_{l}$	$d_{x_{l}}^{2}$	$y_{l}$	$y_{l}$	$d_{y_l} =\overline{y}_{l}-y_{l}$	$d_{y_{l}}^{2}$
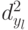
1	0	1,0	1,0	7,0	6,68	-0,32	0,1024
2	0,5	0,5	0,25	4,8	4,94	0,14	0,0196
3	1,0	0	0	2,8	3,2	0,40	0,16
4	1,5	-0,5	0,25	1,4	1,46	0,06	0,0036
5	2,0	-1,0	1,0	0	0,28	0,28	0,0784

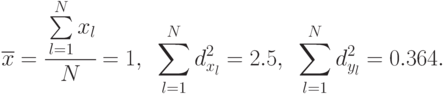
$\overline{x}=\cfrac{\sum\limits_{l=1}^{N}{x_l}}{N}=1,\,\,\, \sum\limits_{l=1}^{N}{d_{x_l}^2} = 2.5,\,\,\, \sum\limits_{l=1}^{N}{d_{y_l}^2} = 0.364.$

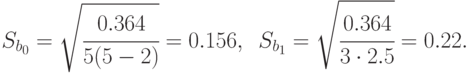
$S_{b_0}=\sqrt{\cfrac{0.364}{5(5-2)}}=0.156,\,\,\, S_{b_1}=\sqrt{\cfrac{0.364}{3\cdot 2.5}}=0.22.$

С уровнем достоверности 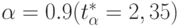$\alpha = 0.9 (t^*_{\alpha } = 2,35)$

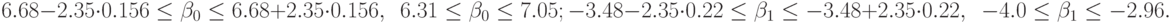
$6.68-2.35\cdot 0.156\le \beta_0\le 6.68+2.35\cdot 0.156,\,\,\, 6.31\le \beta_0\le 7.05;\\ -3.48-2.35\cdot 0.22\le \beta_1\le -3.48+2.35\cdot 0.22,\,\,\, -4.0\le \beta_1\le -2.96.$

Большой размах доверительных границ объясняется малым числом наблюдений в данном эксперименте.

Доверительные границы для y принимают разные значения в зависимости от значений факторов [33].

Дальше >>

Авторизоваться

Компьютерное моделирование

Обработка результатов имитационного эксперимента

5.10. Обработка результатов эксперимента на основе регрессии

Вопросы и ответы