Поиск
Последовательный поиск
Под последовательным поиском мы подразумеваем исследование имен в том
порядке, в котором они встречаются в таблице. При таком поиске в таблице в
худшем случае получается просмотр всей таблицы; даже в среднем последовательный поиск
имеет тенденцию к использованию числа операций, пропорционального  . Для больших таблиц его не следует относить к методам быстрого
поиска, поскольку последовательный поиск асимптотически гораздо медленнее других алгоритмов,
описанных в этой лекции. Несмотря на его низкие асимптотические возможности,
имеется ряд причин, по которым этот метод следует обсудить вначале. Во-первых,
хотя идея его проста, он позволяет нам ввести важные понятия и методы, применимые к
поиску вообще. Во-вторых, последовательный поиск является единственным методом
поиска, применимым к отдельным устройствам памяти и к тем таблицам, которые
строятся на пространстве имен без линейного порядка. Наконец, последовательный
поиск является быстрым для достаточно малых таблиц и для больших таблиц,
организованных иерархическим способом: более быстрый метод используется для
исследования окрестности верхушки иерархии, а последовательный поиск – для
подтаблицы на нижнем уровне иерархии.
. Для больших таблиц его не следует относить к методам быстрого
поиска, поскольку последовательный поиск асимптотически гораздо медленнее других алгоритмов,
описанных в этой лекции. Несмотря на его низкие асимптотические возможности,
имеется ряд причин, по которым этот метод следует обсудить вначале. Во-первых,
хотя идея его проста, он позволяет нам ввести важные понятия и методы, применимые к
поиску вообще. Во-вторых, последовательный поиск является единственным методом
поиска, применимым к отдельным устройствам памяти и к тем таблицам, которые
строятся на пространстве имен без линейного порядка. Наконец, последовательный
поиск является быстрым для достаточно малых таблиц и для больших таблиц,
организованных иерархическим способом: более быстрый метод используется для
исследования окрестности верхушки иерархии, а последовательный поиск – для
подтаблицы на нижнем уровне иерархии.
Для последовательного поиска по таблице 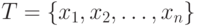 мы предполагаем, что имеется указатель
мы предполагаем, что имеется указатель  , значение
которого принадлежит отрезку
, значение
которого принадлежит отрезку 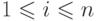 или, возможно,
или, возможно,  . Над этим указателем разрешается производить
только следующие операции; первоначальное присваивание ему значения 1 или
. Над этим указателем разрешается производить
только следующие операции; первоначальное присваивание ему значения 1 или  (или, если удобнее, 0 или
(или, если удобнее, 0 или 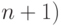 , увеличение и /или
уменьшение его на единицу и сравнение его с 0, 1,
, увеличение и /или
уменьшение его на единицу и сравнение его с 0, 1,  или
или  . При
таких соглашениях наиболее очевидный алгоритм поиска в таблице
. При
таких соглашениях наиболее очевидный алгоритм поиска в таблице  первого вхождения
данного имени
первого вхождения
данного имени  имеет вид алгоритма 13.1. Здесь, как и во всех других
алгоритмах поиска, изложенных в настоящей лекции, мы полагаем, что алгоритм
останавливается немедленно по отыскании
имеет вид алгоритма 13.1. Здесь, как и во всех других
алгоритмах поиска, изложенных в настоящей лекции, мы полагаем, что алгоритм
останавливается немедленно по отыскании  или установлении, что
или установлении, что  в таблице нет.
в таблице нет.
Алгоритм 13.1. Последовательный поиск
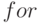

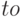





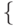 найдено:
найдено:  указывает на
указывает на 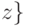
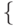 не найдено:
не найдено:  не входит в
не входит в 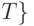
Рассмотрим некоторые аспекты эффективности последовательного поиска, начиная со стандартных методов программирования. В программе, построенной в виде одного цикла, как алгоритм 13.1, любое значительное ускорение должно быть следствием улучшения кода в цикле. Для того чтобы увидеть, какие операции выполняются внутри цикла, необходимо переписать алгоритм 13.1 в форме, близкой к языку машины:
i<-1
цикл: if z = xi then найдено
if i = n then не найдено
i<-i + 1
goto циклЗа каждую итерацию выполняется до четырех команд: два сравнения, одна операция увеличения и одна передача управления.
Для ускорения внутреннего цикла общим приемом является добавление в
таблицу специальных строк, которые делают необязательной явную проверку
того, достиг ли указатель границ таблицы. Это можно сделать в алгоритме
13.1. Если перед поиском мы добавим искомое имя  в конце
таблицы, то цикл всегда будет завершаться отысканием вхождения
в конце
таблицы, то цикл всегда будет завершаться отысканием вхождения  ; таким
образом, нам не нужно в цикле каждый раз делать проверку
; таким
образом, нам не нужно в цикле каждый раз делать проверку 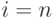 . В конце цикла
проверка условия
. В конце цикла
проверка условия  , выполняемая лишь однажды, говорит о
том, является ли найденное вхождение
, выполняемая лишь однажды, говорит о
том, является ли найденное вхождение  истинным или специальным
элементом таблицы. Это демонстрируется в алгоритме 13.2.
истинным или специальным
элементом таблицы. Это демонстрируется в алгоритме 13.2.

i<-1
while z !=xi do i <-i+1
if i<=n then{найдено: i указывает на z}
else{не найдено}Алгоритм 13.2. Улучшенный последовательный поиск
Улучшение алгоритма 13.1 будет наиболее очевидным, если мы перепишем алгоритм 13.2 в тех же близких к языку машины обозначениях, которые использовались раньше:
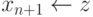
i<-1
цикл: if z = xi then goto возможно
i<-i+1
goto цикл
возможно: if i<=n then {найдено:i указывает на z}
else{не найдено}При каждой итерации выполняются лишь три действия вместо четырех, как это было в алгоритме 13.1. Таким образом, в большинстве вычислительных устройств цикл в алгоритме 13.2 будет выполняться гораздо быстрее, чем в алгоритме 13.1, и поскольку скорость цикла определяет скорость всей программы, такое же сравнение имеет место для двух программ.
Печально то, что фокус с добавлением  в конец таблицы
перед поиском удается, только если мы имеем прямой
непосредственный доступ к концу таблицы. Это возможно, если таблица хранится в
памяти с произвольным доступом, но невозможно в общем случае, когда
используется
связанное размещение или память с последовательным доступом.
в конец таблицы
перед поиском удается, только если мы имеем прямой
непосредственный доступ к концу таблицы. Это возможно, если таблица хранится в
памяти с произвольным доступом, но невозможно в общем случае, когда
используется
связанное размещение или память с последовательным доступом.
Единственным недостатком алгоритма 13.2 является то, что при безуспешном
поиске (поиске имен, которых нет в таблице) всегда просматривается вся
таблица. Если
такой поиск возникает часто, то имена надо хранить в естественном порядке; это
позволяет завершать поиск, как только при просмотре попалось первое имя,
большее
или равное аргументу поиска. В этом случае в конец таблицы следует добавить
фиктивное имя  для того, чтобы гарантировать выполнение
условия завершения (
для того, чтобы гарантировать выполнение
условия завершения (  - это новое имя, которое по
предположению больше любого имени из пространства
имен
- это новое имя, которое по
предположению больше любого имени из пространства
имен  ). Таким образом получаем алгоритм 13.3.
). Таким образом получаем алгоритм 13.3.

i<-1
while z > xi do i <- i+1
if z=xi then{найдено:i указывает на z}
else{не найдено}Алгоритм 13.3.Последовательный поиск по таблице, хранимой в естественном порядке
Логарифмический поиск в статических таблицах
Мы говорим о логарифмическом времени поиска, как только возникает
возможность за время  , не зависящее от
, не зависящее от  ,
последовательно свести задачу поиска в таблице, содержащей
,
последовательно свести задачу поиска в таблице, содержащей  имен, к задаче поиска в таблице, содержащей не более
имен, к задаче поиска в таблице, содержащей не более  имен, где
имен, где  - константа. В этом случае время
- константа. В этом случае время  , требующееся для поиска в таблице с
, требующееся для поиска в таблице с  именами,
удовлетворяет рекуррентному соотношению
именами,
удовлетворяет рекуррентному соотношению
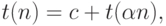
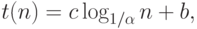
 определяется начальными условиями и коэффициент
определяется начальными условиями и коэффициент  при логарифме
есть время, требуемое для уменьшения размера таблицы от
при логарифме
есть время, требуемое для уменьшения размера таблицы от  до
до  .
.Самыми распространенными предположениями, которые дают возможность
уменьшить размер таблицы от  до
до 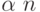 за время, не зависящее от
за время, не зависящее от  , являются предположения о том, что
пространство имен
, являются предположения о том, что
пространство имен  линейно упорядочено и что сравнение двух имен
линейно упорядочено и что сравнение двух имен 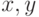 из
из  (для определения
(для определения 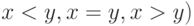 есть элементарная операция, требующая постоянного количества
времени, не
зависящего от
есть элементарная операция, требующая постоянного количества
времени, не
зависящего от  . В результате время, необходимое для большинства
логарифмических алгоритмов
поиска,естественно измеряется числом сравнений (с тремя исходами) пар имен. Для
некоторых алгоритмов, однако, более естественны сравнения с большим, но
фиксированным числом исходов.
. В результате время, необходимое для большинства
логарифмических алгоритмов
поиска,естественно измеряется числом сравнений (с тремя исходами) пар имен. Для
некоторых алгоритмов, однако, более естественны сравнения с большим, но
фиксированным числом исходов.
В этом разделе мы рассматриваем только статические таблицы, то есть таблицы, в которых включение и исключение либо не встречаются, либо так редки, что когда они появляются, строится новая таблица. Динамические структуры таблиц, допускающие логарифмическое время поиска, так же как и эффективные алгоритмы включения и исключения, обсуждаются в конце этой лекции. Для статических таблиц нужно обсудить лишь алгоритмы поиска и построения таблицы. Алгоритмы поиска достаточно просты, но некоторые из алгоритмов построения таблицы сложны. Такая ситуация возникает потому, что в случае статической таблицы разумно считать частоты обращения известными, и, может быть, стоит затратить существенные усилия на построение оптимальной таблицы – таблицы с минимальным средним временем поиска (относительно данных частот обращения). Алгоритмы построения таблиц и их анализ являются наиболее важными темами этого раздела.
