|
Подскажите, пожалуйста, планируете ли вы возобновление программ высшего образования? Если да, есть ли какие-то примерные сроки? Спасибо! |
Моделирование в GPSS World
6.3. Решение прямой и обратной задач в системе моделирования
При имитационном моделировании с использованием специальных инструментальных средств, например, GPSS World, в общем случае решаются две задачи. Назовем их прямой и обратной.
Прямая задача заключается в нахождении оценки математического ожидания какого-либо параметра моделируемой системы при заданном времени ее функционирования.
Обратная задача состоит в определении оценки математического ожидания времени функционирования моделируемой системы, за которое какой-либо ее показатель достигает заданного значения.
Решение этих задач, особенно обратной задачи, имеет свои особенности. Рассмотрим эти особенности на примере.
6.3.1. Постановка прямой и обратной задач
Пример 6.1. Сервер обрабатывает запросы, поступающие с автоматизированных рабочих мест (АРМ) с интервалами, распределенными по показательному закону со средним значением T1= 2 мин. Вычислительная сложность запросов распределена по нормальному закону с математическим ожиданием S1 = 6 x 107 оп и среднеквадратическим отклонением S2 = 2*105 Производительность сервера Q = 6*105 оп /c. В случае занятости сервера поступающий запрос теряется.
Сервер представляет собой однофазную систему массового обслуживания разомкнутого типа с отказами.
Прямая задача.Построить имитационную модель для определения оценки математического ожидания количества запросов (дальше - количества запросов), обработанных сервером за время функционирования T = 1 час, и оценки математического ожидания вероятности обработки запросов (дальше - вероятности обработки запросов).
Обратная задача.Построить имитационную модель для определения оценки математического ожидания времени (дальше - времени обработки), за которое будет обработано сервером N запросов, и оценки математического ожидания вероятности обработки запросов.
6.3.2. Решение прямой задачи
Рассчитаем количество прогонов, которые нужно выполнить в каждом наблюдении, т. е. проведем так называемое тактическое планирование эксперимента. Пусть результаты моделирования (вероятность обработки запросов) нужно получить с доверительной вероятностью 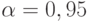 и точностью
и точностью 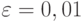 . Расчет проведем для худшего случая, т. е. при вероятности
. Расчет проведем для худшего случая, т. е. при вероятности 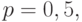 так как до эксперимента
так как до эксперимента  неизвестно:
неизвестно:
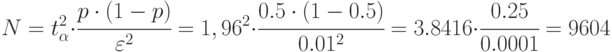
В модели для имитации источника запросов следует использовать блок GENERATE, для имитации сервера как одноканального устройства - блоки SEIZE и RELEASE, для имитации обработки запросов - блок ADVANCE.
В модели должны быть следующие элементы:
- задание исходных данных;
- описание арифметических выражений;
- сегмент имитации поступления и обработки запросов;
- сегмент задания времени моделирования и расчета результатов моделирования.
Серверу дадим имя Server. Для вывода из модели транзактов, имитирующих обработанные и потерянные запросы, используем блоки TERMINATE с метками ObrZap и PotZap соответственно. Для счета количества всех запросов используем метку KolZap.
6.3.2.1. Блок-диаграмма модели
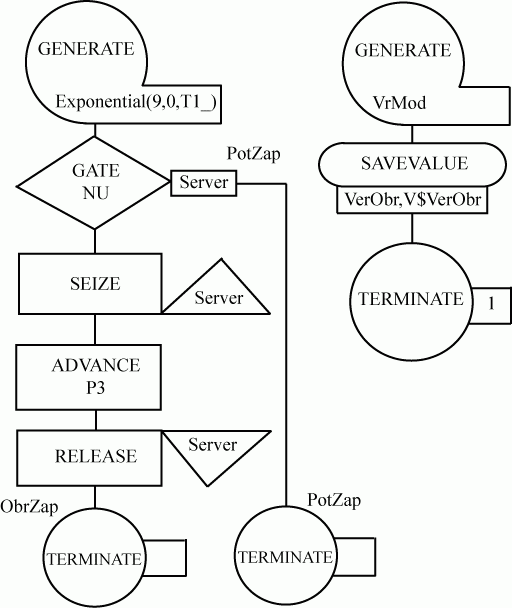
Построим блок-диаграмму модели для решения прямой задачи, т. е. сегмент имитации поступления и обработки запросов и сегмент задания времени моделирования и расчета результатов моделирования (рис. 6.1).
Блок-диаграмма представляет собой набор стандартных блоков [5]. Она строится так. Из множества блоков выбирают нужные и далее выстраивают их в диаграмму для того, чтобы в процессе функционирования модели они как бы взаимодействовали друг с другом. Диаграмма сопровождается необходимыми комментариями. Использование блоков при построении моделей зависит от логических схем работы реальных систем, моделируемых на ЭВМ.
Теперь приступим к написанию программы модели.
6.3.2.2. Программа модели
Для задания исходных данных используем переменные пользователя. Они задаются с помощью команды EQU. Переменным пользователя даны такие же имена, как и в постановке задачи, но добавлен знак подчеркивания. Например, T1_, S1_ и т. д. Время моделирования зададим переменной пользователя VrMod.
Арифметическая переменная для расчета времени обработки VrObr запроса на сервере:
VrObr VARIABLE (Normal(2,S1_#Koef,S2_#Koef))/Q_
Переменная пользователя Koef введена для удобства изменения (пропорционального изменения) характеристик нормального закона распределения, которому подчиняется вычислительная сложность запросов. Особенно целесообразно использование этой переменной при проведении экспериментов. Примеры применения приведены в "Организация компьютерных экспериментов" .
Вероятность обработки VerObr запросов на сервере будем определять как отношение количества обработанных N$ObrZap запросов к количеству всего поступивших N$KolZap запросов:
VerObr VARIABLE N$ObrZap/N$KolZap
В арифметическом выражении VerObr, например, N$ObrZap - системный числовой атрибут - количество транзактов, вошедших в блок с меткой ObrZap, а N$KolZap - количество транзактов, вошедших в блок с меткой KolZap.
Все необходимое для написания программы модели имеется. Напишем программу решения прямой задачи.
; Обработка запросов сервером. Прямая задача ; Задание исходных данных T1_ EQU 120 ; Средний интервал поступления запросов, с S1_ EQU 60000000 ; Среднее значение вычислительной сложности запросов, оп S2_ EQU 200000 ; Стандартное отклонение вычислительной сложности запросов, оп Q_ EQU 600000 ; Среднее значение производительности сервера, оп/с Koef EQU 1 ; Коэффициент изменения характеристик нормального распределения VrObr VARIABLE (Normal(2,(S1_#Koef),(S2_#Koef))/Q_ VerObr VARIABLE N$ObrZap/N$KolZap VrMod EQU 3600 ; Время моделирования, 1 ед. мод. времени = 1 с. ; Сегмент имитации обработки запросов GENERATE (Exponential(1,0,T1_)) ; Источник запросов KolZap GATE NU Server,PotZap ; Свободен ли сервер? Если да, то SEIZE Server ; занять сервер ADVANCE V$VrObr ; Имитация обработки запроса RELEASE Server ; Освободить сервер ObrZap TERMINATE ; Обработанные запросы PotZap TERMINATE ; Потерянные запросы ; Сегмент задания времени моделирования и расчета результатов GENERATE VrMod TEST L X$Prog,TG1,Met1 ; Если X$Prog < TG1, SAVEVALUE Prog,TG1 ; то X$Prog = TG1 Met1 TEST E TG1,1,Met2 ; Если TG1 = 1, то SAVEVALUE VerObr, V$VerObr ; расчет и сохранение в ячейке VerObr вероятности обработки запросов SAVEVALUE Res,(INT(N$ObrZap/X$Prog)) ; расчет и сохранение в ячейке Res количества обработанных запросов Met2 TERMINATE 1 START 1000,NP ; Прогоны до установившегося режима RESET ; Сброс накопленной статистики START 9604 ; Количество прогонов модели
При расчете количества обработанных запросов
SAVEVALUE Res,(INT(N$ObrZap/X$Prog))
в арифметическом выражении N$ObrZap/X$Prog используется число прогонов. В арифметическом выражении указано не явное число прогонов, а в виде содержимого ячейки X$Prog. Число прогонов заносится предварительно в эту ячейку по завершении первого прогона модели, но до того момента, когда из счетчика завершений TG1 будет вычтена первая единица. В этом случае арифметическое выражение не зависит от числа прогонов, которое может меняться на различных этапах создания и эксплуатации модели, в том числе и в зависимости от исходных данных, а также от точности и достоверности результатов моделирования. Поскольку количество обработанных запросов не может быть дробным числом, то для получения целого числа, записываемого в ячейку Res, используется процедура INT из встроенной библиотеки.
Для уменьшения машинного времени расчет искомых показателей производится не после каждого прогона, а после завершения последнего прогона, т. е. когда содержимое счетчика завершений будет равно единице ( TG1 = 1 ).
6.3.2.3. Ввод текста программы модели, исправление ошибок и проведение моделирования
- Запустите GPSS World.
- Закройте окно напоминания о необходимости обновления "Заметок". Откроется главное меню.
- Для ввода текста GPSS World имеет текстовый редактор. Откройте окно текстового редактора. Для этого выберите в меню File / New и в появившемся меню выберите Model. Нажмите Ok.
- Наберите текст программы модели, т. е. создайте объект "Модель". При вводе текста следует использовать клавишу [Tab]. Например, после набора Т1_ нужно нажать клавишу [Tab]. Интервалы табуляции установлены по умолчанию.
- После ввода текста программы модели создайте объект "Процесс моделирования", представляющий собой оттранслированный объект "Модель". Для трансляции объекта "Модель" выберите Command / Creat e Simulation. По этой команде транслятор GPSS проверяет текст программы модели на наличие синтаксических ошибок.
- При наличии синтаксических ошибок транслятор в окне JOURNAL выдаст список сообщений об ошибках трансляции. Перейдите к п. 7. При отсутствии ошибок в окне JOURNAL появится сообщение Model Translation Begun. Ready. Перейдите к п. 9.
- Исправьте ошибки. Для поиска ошибок в тексте программы модели и их исправления используйте команду Search / Next Error. При первом выполнении этой команды курсор мыши помещается в строке текста модели с ошибкой. После исправления первой ошибки вновь используйте команду Search / Next Error и т.д. столько раз, сколько ошибок в тексте программы.
- После исправления ошибок перейдите к п.5.
- Сохраните модель. Для этого выберите в главном меню File / Save As. Дайте модели имя Модель процессов изготовления изделий и нажмите Ok.
- Откликом в данной модели является вероятность обработки запросов сервером. Рассчитаем количество прогонов модели при среднеквадратическом отклонении для худшего случая при точности
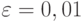 , и доверительной вероятности
, и доверительной вероятности 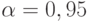 :
: - Запустите модель. Для этого в главном меню выберите Command / Start и в диалоговом окне вместо 1 наберите 9604. Нажмите Ok.
- При наличии логических ошибок для их поиска в тексте программы модели и исправления используйте команду Search / Goto Line столько раз, сколько ошибок указано в окне JOURNAL. Там же (в окне JOURNAL ) указаны номера строк с ошибками.
- При отсутствии логических ошибок в модели по окончании ее работы система GPSS World автоматически создает стандартный отчет, который появится в окне Report. В окне будут содержаться следующие данные:
- об именах объектов модели;
- блоках модели;
- ОКУ и МКУ;
- очередях;
- сохраняемых величинах.
В результате решения прямой задачи получим, что за один час сервером будет обработано N=16 запросов, а вероятность обработки составит VerObr = 0,546. Если не использовать процедуру INT - выделения целого числа с отбрасыванием дробной части, будет обработано 16,345 запроса.
6.3.3. Решение обратной задачи
Для решения обратной задачи возьмем количество запросов, ожидаемое время обработки которых нужно определить, N =16 - результат решения прямой задачи.
Программа модели приведена ниже.
; Обработка запросов сервером. Обратная задача ; Задание исходных данных T1_ EQU 120 ; Средний интервал поступления запросов, с S1_ EQU 60000000 ; Среднее значение вычислительной сложности запросов, оп S2_ EQU 200000 ; Стандартное отклонение вычислительной сложности запросов, оп Q_ EQU 600000 ; Среднее значение производительности сервера, оп/c Koef EQU 1 ; Коэффициент изменения характеристик нормального распределения Koef1 EQU 1 ; Коэффициент учета дробной части N_ EQU 16 ; Количество запросов ; Сегмент имитации обработки запросов GENERATE (Exponential(1,0,T1_)) ; Источник запросов KolZap GATE NU Server,PotZap ; Свободен ли сервер? Если да, то SEIZE Server ; занять сервер ADVANCE ((Normal(2,(S1_#Koef),(S2_#Koef)))/Q_) ; Имитация обработки запроса RELEASE Server ; Освободить сервер TRANSFER ,ObrZap ; Запрос отправляется в сегмент завершения моделирования PotZap TERMINATE ; Потерянные запросы ; Сегмент организации завершения моделирования и расчета результатов ObrZap TEST L X$Prog,TG1,Met1 ; Если X$Prog < TG1, SAVEVALUE Prog,TG1 ; то X$Prog = TG1 SAVEVALUE NZap,0 ; Обнуление счетчика обработанных запросов Met1 SAVEVALUE NZap+,1 ; Счет количества обработанных запросов TEST E X$NZap,N_,Ter1 ; Если X$NZap = N_, то TEST E TG1,1,Met2 ; если TG1 = 1, то SAVEVALUE VerObr,(N$ObrZap/N$KolZap) ; расчет и сохранение в ячейке VerObr вероятности обработки запросов SAVEVALUE TimeNZap,((AC1-X$AC2)/(X$Prog#Koef1)) ;расчет и сохранение в ячейке TimeNZap времени обработки запросов SAVEVALUE AC2,AC1 ; Запомнить абсолютное модельное время в ячейке АС2 Met2 SAVEVALUE NZap,0 ; Обнуление счетчика обработанных запросов TERMINATE 1 Ter1 TERMINATE START 1000,NP ; Прогоны до установившегося режима RESET ; Сброс накопленной статистики START 9604 ; Количество прогонов модели
При решении обратной задачи один прогон определяется заданным количеством запросов N_, а не временем моделирования. Для этого организован счетчик обработанных запросов в виде сохраняемой ячейки NZap. Как только содержимое X$NZap = N_, из счетчика завершений вычитается единица.
Для расчета времени обработки заданного количества запросов используется арифметическое выражение (AC1-X$AC2)/X$Prog. В состав этого выражения входят абсолютное модельное время АС1 и опять количество прогонов. Запоминается количество прогонов также как и при решении прямой задачи.
Кроме этого, в арифметическом выражении есть сохраняемая ячейка X$AC2. Дело в том, что команда RESET не влияет на абсолютное модельное время АС1. Время же выполнения 1000 прогонов до установившегося режима не должно участвовать в расчете. Поэтому оно запоминается, а затем вычитается из абсолютного модельного времени выполнения 1000 + 9604 = 10604 прогонов. Количество прогонов до установившегося режима может быть и другим.
В результате моделирования получим время обработки 16 запросов 3523,658 с.
Фрагмент из отчета моделирования приведен ниже:
SAVEVALUE RETRY VALUE PROG 0 9604.000 NZAP 0 0 VEROBR 0 0.546 TIMENZAP 0 3523.658
А почему не 3600 с? Ведь это же время моделирования было задано при решении прямой задачи. Потому что мы отбросили дробную часть, т. е. взяли 16, а не 16,345. Как же поступить, чтобы учесть и отброшенную дробную часть? Ведь в счетчике фиксируются обработанные запросы только целыми числами, а не дробными?
Для учета десятых долей дробной части зададим N_ = 163, т. е. увеличим в 10 раз. Это нужно учесть и в арифметическом выражении: ((AC1-X$AC2)/(X$Prog#Koef1)). Переменной пользователя Koef1 задается значение 10. По завершении моделирования получим 3586,504. Этот результат уже ближе к 3600.
Для учета сотых долей дробной части зададим N_ = 1634, а Koef1 = 100. Получим 3595,399 с.
Вероятность обработки запросов во всех случаях практически одна и та же, т. е. 0,546. Однако время моделирования существенно возрастает: 4 с, 39 с и 6 мин 29 c, т. е. в 10 и 100 раз соответственно.
В примере решения обратной задачи также показано, что арифметические выражения можно не описывать отдельно до блоковой части программы вместе с заданием исходных данных (как в модели прямой задачи), а сразу записывать в соответствующих блоках, заключив в скобки (скобки можно и не ставить, но лучше это делать).
Например (см. сегмент организации завершения моделирования и расчета результатов):
ADVANCE ((Normal(2,(S1_#Koef),(S2_#Koef)))/Q_) ; Розыгрыш времени обработки запроса SAVEVALUE VerObr,(N$ObrZap/N$KolZap)) ; Расчет вероятности обработки запросов SAVEVALUE TimeNZap,((AC1-X$AC2)/(X$Prog#Koef1)) ;Расчет среднего времени обработки запросов