|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Электронная подпись. Протоколы SSH, SSL
Электронная подпись
В конце любого письма мы привыкли ставить подпись, чтобы уведомить получателя о том, кто является отправителем данного документа. Кроме того, подпись ответственного лица придает документу юридическую силу. По мере внедрения электронных средств доставки документов (факс и электронная почта) проблема их достоверности обрела крайнюю актуальность. Ведь копирование любой последовательности бит или пикселей не представляет никакой трудности. Современные телекоммуникационные каналы уязвимы для перехвата и искажения пересылаемых документов.
Рассмотрим сначала, от каких действий злоумышленника должна защищать система идентификации.
- Отказ от выполненных действий. Субъект утверждает, что он не посылал некоторый документ, хотя на самом деле он его послал.
- Модификация документа. Получатель модифицирует полученный документ и утверждает, что именно такую версию документа он и получил.
- Подделка. Субъект фабрикует сообщение и утверждает, что оно ему прислано.
- Перехват. Злоумышленник С перехватывает сообщение, посланное А к В с целью модификации.
- Маскировка. Посылка сообщения от чужого имени.
- Повтор. Злоумышленник С посылает повторно сообщение от А к Б, перехваченное им ранее.
Решение практически всех этих проблем может быть реализовано с помощью электронной подписи, базирующейся на алгоритме RSA или другом асимметричном алгоритме. Рассмотрим принципы, на которых базируется электронная подпись.
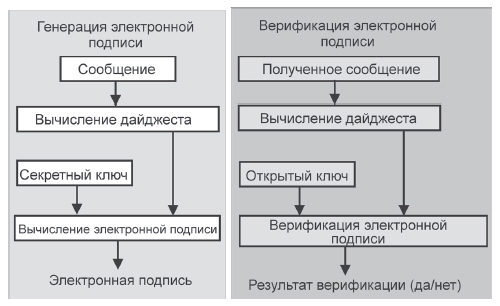
Пусть имеются секретные коды d, p и q, а также открытые e и n=pq. Пусть также А передает сообщение DATA адресату Б. Электронная подпись отправителя А базируется на его секретном ключе и открытом ключе получателя Б. Сначала отправитель с помощью хэш-функции (например, SHS — Secure Hash Standard; http://www.nist.gov/itl/div897/pubs/fip180-1.htp) генерирует дайджест своего сообщения длиной 160 бит (5 слов). Затем с помощью своего секретного ключа он шифрует дайджест и формирует электронную подпись. При этом А не может отказаться от того, что именно он послал сообщение, так как только он знает свой секретный ключ. Электронную подпись нельзя использовать повторно и подписанный документ нельзя модифицировать, так как любые модификации неизбежно изменят его дайджест, а, следовательно, и электронную подпись. Получатель с помощью открытого ключа отправителя дешифрует код электронной подписи, а затем с использованием дайджеста проверяет ее корректность.
Национальный институт стандартов США принял стандарт DSS (Digital Signature Standard; http://www.itl.nist.gov/div897/pubs/fip198.htm), в основу которого легли алгоритмы Эль-Гамаля и RSA. В России для этой цели используется алгоритм ГОСТ Р 34.10-2001.
Рассмотрим алгоритмы вычисления дайджеста сообщения, электронной подписи и идентификации отправителя. Начнем с алгоритма SHA (Secure Hash Algorithm).
Сначала сообщение разбивается на блоки длиной 512 бит. Если длина сообщения не кратна 512, к последнему блоку приписывается справа 1, после чего он дополняется нулями до 512 бит. В конец последнего блока записывается код длины сообщения. В результате сообщение приобретает вид n 16-разрядных двоичных слов M1,M2,…,Mn. M1 содержит первый символ.
Алгоритм SHA использует 80 логических функций f0,f1,…,f79, которые производят операции над тремя 32-разрядными словами ( B,C,D ):
ft(B,C,D) = (B AND C) OR ((NOT B) AND D) для 0 <= t <= 19 ft(B,C,D) = B XOR C XOR D для 20 <= t <= 39 ft(B,C,D) = (B AND C) OR (B AND D) OR (C AND D) для 40 <= t <= 59 ft(B,C,D) = B XOR C XOR D для 60 <= t <= 79
В алгоритме используется также 80 констант K1,K2,…, K79:
Kt = 5A827999 для 0 <= t <= 19 Kt = 6ED9EBA1 для 20 <= t <= 39 Kt = 8F1BBCDC для 40 <= t <= 59 Kt = CA62C1D6 для 60 <= t <= 79
Вводится 5 переменных Hi, инициализируемых как:
H0 = 67452301 H1 = EFCDAB89 H2 = 98BADCFE H3 = 10325476 H4 = C3D2E1F0
Массив M делится на группы из 16 слов W0, W1,…,W15 ( W0 самое левое слово).
Для t = 16 - 79 wt = S1(Wt-3 XOR Wt-8 XOR Wt-14 XOR Wt-16)
Ak означает операцию циклического сдвига влево на k разрядов.
Пусть теперь A = H0, B = H1, C = H2, D = H3, E = H4.
for t = 0 to 79 do
TEMP = S5(A) + ft(B,C,D) + E + Wt + Kt. ( TEMP — временная переменная).
E = D; D = C; C = S30(B); B = A; A = TEMP;
Пусть H0 = H0 + A; H1 = H1 + B; H2 = H2 + C; H3 = H3 + D; H4 = H4 + E.
В результате обработки массива М будет получено 5 слов H0, H1, H2, H3, H4 с общей длиной 160 бит, которые и образуют дайджест сообщения. Полученная кодовая последовательность с высокой степенью уникальности характеризует сообщение. Любое редактирование сообщения практически неизбежно приведет к изменению дайджеста. Поскольку алгоритм вычисления дайджеста общеизвестен, он не может рассматриваться как гарантия предотвращения модификации сообщения. Смысл вычисления дайджеста заключается в уменьшении объема данных, подлежащих шифрованию. Для того, чтобы превратить дайджест в электронную подпись, надо воспользоваться секретным ключом. Схема реализации алгоритма DSS (Digital Signature Standard) показана на рис. 15.1.
DSS использует следующие параметры (http://www.itl.nist.gov/div897/pubs/fip186.htm):
p — простое число, которое при 512<= L <= 1024 удовлетворяет условию 2L-1 < p < 2L, L кратно 64.
q — простой делитель p-1, где 2159 < q < 2160.
g = h(p-1)/q mod p, где h — любое целое, для которого 1 < h < p-1 и h(p-1)/q mod p > 1.
x равно случайному или псевдослучайному целому числу, для которого 0 < x < q.
y = gx mod p.
k равно случайному или псевдослучайному целому числу, для которого 0 < k < q.
Целые p, q и g могут быть общедоступными и использоваться группой пользователей. Секретным и открытым ключами являются х и у, соответственно. Параметры х и k применяются только для формирования электронной цифровой подписи и должны храниться в секрете. Параметр k генерируется для каждой подписи.
Подпись сообщения M представляет собой два числа r и s, вычисленные согласно формулам:
r = (gk mod p) mod q
s = (k-1(SHA(M) + xr)) mod q. (здесь k-1 — величина, обратная k).
SHA(M) представляет собой дайджест сообщения M (160-битовая строка). После вычисления r и s следует проверить, не равно ли одно из них нулю.
Для верификации электронной подписи проверяющая сторона должна иметь параметры p, q и g, а также открытый ключ отправителя (подписанта) y.
Пусть M', r' и s' представляют собой полученное сообщение и электронную подпись. Получатель начинает верификацию с проверки условия 0 < r' < q и 0 < s' < q. Если хотя бы одно из условий не выполнено, электронная подпись некорректна. Далее производится вычисление:
w = (s')-1 mod q u1 = ((SHA(M')w) mod q u2 = ((r')w) mod q v = (((g)u1 (y)u2) mod p) mod q.
Если v = r', верификация подписи завершилась успешно и получатель может с высокой вероятностью быть уверен, что он получил сообщение от партнера, владеющего секретным ключом х, соответствующим открытому ключу у. Если же v не равно r', то сообщение было модифицировано или подписано самозванцем.
Алгоритм Диффи-Хелмана
Алгоритм Диффи-Хелмана (1976 год) использует функцию дискретного возведения в степень и похож на метод Эль-Гамаля (см. RFC-2631).
Сначала генерируются два больших простых числа n и q. Эти два числа не обязательно хранить в секрете. Далее один из партнеров P1 генерирует случайное число x и посылает другому участнику будущих обменов P2 значение
A = qx mod n
По получении А партнер P2 генерирует случайное число у и посылает P2 вычисленное значение
B = qy mod n
Партнер P1, получив В, вычисляет Kx = Bx mod n, а партнер P2 вычисляет Ky = Ay mod n. Алгоритм гарантирует, что числа Ky и Kx равны и могут быть использованы в качестве секретного ключа для шифрования. Ведь даже перехватив числа А и В, трудно вычислить Kx или Ky.
Алгоритм Диффи-Хелмана, обеспечивая конфиденциальность передачи ключа, не может гарантировать, что он прислан именно тем партнером, который предполагается. Для решения этой проблемы был предложен протокол STS (station-to-station). Этот протокол для идентификации отправителя использует технику электронной подписи. Подпись шифруется общим секретным ключом, после того как он сформирован. Подпись включает в себя идентификаторы как P1, так и P2. (см. также RFC-2786 "Diffie-Helman USM Key Management Information Base and Textual Convention. M. St. Johns. March 2000".)