НОУ ИНТУИТ | Нейроинформатика. Лекция 6: Погрешности в нейронных сетях

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 01.03.2007 | Уровень: специалист | Доступ: свободно

Вам нравится? Нравится 29 студентам

| Поделиться |

Поддержать программу

Аннотация: Подробно излагается и рассматривается алгоритм оценки погрешностей в работе нейронных сетей

Ключевые слова: вектор, интервальная оценка, back, propagate, устойчивость, компьютерная модель, операции, синапс, очередь, связь, сеть, интервал, погрешность, ПО, вероятность, место, нелинейный преобразователь, точка ветвления, нейрон, погрешности вычислений, входной, функция, отрезок, функция активации, вес, максимум, сумматор, градиент функции, минимум, значение, прямой, вычисление, разность, нейросеть, нейронная сеть, случайная величина, дисперсия, выходной нейрон, обучающая выборка, входные данные, метод обратного распространения ошибки

Погрешности в нейронных сетях

ВЦК СО РАН, КГУ

А.Н. Горбань, М.Ю. Сенашова

Рассматриваются нейронные сети слоистой структуры, состоящие из слоев стандартных нейронов. Изучаются ошибки, возникающие при технической реализации сетей, а также при шумах и повреждениях.

Определены максимально допустимые погрешности, возможные для сигналов и параметров каждого элемента сети, исходя из условия, что вектор выходных сигналов сети должен вычисляться с заданной точностью. Используются два типа оценок погрешности: гарантированные интервальные оценки и среднеквадратические оценки погрешностей.

Показано, что оценки допустимых погрешностей можно получить в ходе специального процесса "обратного распространения точности". Он состоит в функционировании сети с той же системой связей, но от выходов к входам и с заменой элементов на двойственные. Эта двойственность принципиально отличается от той, которая используется в классическом методе вычисления градиентов оценки с помощью обратного распространения ошибок (back propagation of errors).

С помощью полученных результатов объясняется наблюдаемая высокая устойчивость нейронных сетей к шумам и разрушениям.

Введение

В настоящее время существуют различные технические реализации нейронных сетей, в том числе нейроимитаторы, то есть компьютерные модели нейронных сетей. Нейроимитаторы являются гибкими средствами для изучения сетей и работы с ними. С нейроимитаторами можно выполнять различные операции - обучать, определять наиболее и наименее значимые связи, контрастировать, то есть удалять наименее значимые связи и т. д.

Существует подход, получающий все большее распространение, при котором сначала конструируется и обучается нейроимитатор, а затем создается техническая реализация полученной нейросети с уже вычисленными весами синапсов.

Нейроимитатор, работающий на универсальных цифровых ЭВМ, позволяет вычислять веса синапсов с большой точностью, которую трудно получить при других технических реализациях сети (в первую очередь -аналоговых) в силу ограниченной точности технических устройств. Поэтому возникает задача приведения весов синапсов к некоторому набору конкретных значений. Ее частный случай - задача бинаризации, то есть задача приведения весов синапсов к значениям 0 или 1 (связь либо есть, либо нет - без всяких весов синапсов).

При аналоговых реализациях, различных упрощениях архитектуры (в том числе - бинаризации) технически сложно получить результат работы сети той же точности, что и результат работы нейроимитатора [6.3, 6.4, 6.5]. Поэтому следует ограничится некоторой точностью, с которой может работать сеть, то есть выбрать интервал, в котором могут изменяться значения вектора выходных сигналов сети.

Оценка погрешностей сигналов сети очень полезна при решении задачи упрощения нейронной сети. Зная допустимую погрешность выходного сигнала какого-либо элемента сети, мы можем заменять его более простыми, но менее точными элементами так, чтобы в итоге ошибка не превышала заданную.

Хорошо известно, что нейронные сети могут проявлять исключительную устойчивость к помехам и разрушениям. Иногда эти эффекты называют голографическими свойствами нейронных сетей, подразумевая, что полезные навыки распределены по сети примерно так же, как изображение - по голографической пластинке, и могут сохраняться при значительных разрушениях.

Как будет показано ниже, при прямом прохождении сигналов по достаточно большой сети погрешности гасятся: при больших погрешностях входных сигналов выходные сигналы сети могут иметь сравнительно малые погрешности. Это объясняет устойчивость нейронных сетей к шумам и повреждениям.

Два базовых подхода к оценкам погрешности

Рассмотрим два подхода к решению задачи вычисления погрешностей сигналов сети. При первом подходе ( гарантированные интервальные оценки ) вычисляются допустимые интервалы для погрешностей сигналов сети такие, что погрешность вектора выходных сигналов гарантированно (с вероятностью 1 ) не превышает заданную. При втором подходе ( среднеквадратические оценки погрешностей ) вычисляются среднеквадратические отклонения погрешностей сигналов. При этом часто используется предположение о том, что погрешности различных сигналов являются независимыми случайными величинами.

Существует принципиальное различие между этими двумя типами оценок. Гарантированные интервальные оценки исходят из рассмотрения наихудших возможных случаев, сколь бы малой не была их вероятность. Поэтому они, как правило, завышают реально имеющую место ошибку и слишком пессимистичны с практической точки зрения. Среднеквадратичные оценки, наоборот, стирают возможные большие уклонения и могут оказаться слишком оптимистичными.

Важное различие между двумя типами оценок демонстрируют следующие формулы сложения.

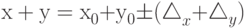Формула сложения для интервальных оценок. Пусть для двух величин x, y определены гарантированные интервалы значений ${\rm{x = x}}_0 {\rm{\pm \bigtriangleup}}_x$ , ${\rm{y = y}}_0 {\rm{\pm \bigtriangleup}}_y$ . Тогда для их суммы имеем гарантированную оценку: ${\rm{x + y = x}}_0 {\rm{+ y}}_0 {\rm{\pm (\bigtriangleup}}_x {\rm{+ \bigtriangleup}}_y {\rm{)}}$ , то есть ${\rm{\bigtriangleup}}_{x + y}{\rm{ = \bigtriangleup}}_x {\rm{+ \bigtriangleup}}_y$ .
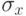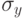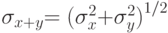Формула сложения для среднеквадратичных уклонений. Пусть для двух независимых величин x, y определены среднеквадратичные уклонения $\sigma_x$ , $\sigma_y$ . Тогда $\sigma_{x + y}{\rm{ = (}}\sigma_x^2 {\rm{+ }}\sigma_y^2 {\rm{)}}^{1/2}$ .

Структура сети

Предполагаем, что сеть имеет слоистую структуру. Это самоограничение позволит несколько сократить изложение, но не влияет на общность рассмотрения - исследование любой сети может быть формально сведено к изучению слоистых сетей.

Сеть слоистой структуры состоит из слоев стандартных нейронов, связанных между собой синапсами с весами, полученными при обучении. Причем сигналы передаются только в одном направлении, с предыдущего слоя на следующий. Под стандартным нейроном [6.1, 6.2] понимается набор элементов, состоящий из адаптивного сумматора, нелинейного преобразователя и точки ветвления ( рис. 6.1). Точка ветвления - это элемент, посылающий выходной сигнал нелинейного преобразователя на вход нескольких стандартных нейронов следующего слоя.

Рис. 6.1. Стандартный нейрон

Так как мы имеем дело с сетями слоистой структуры, состоящими из слоев стандартных нейронов, то выходные сигналы одного слоя являются входными сигналами другого слоя. В свою очередь, внутри самого стандартного нейрона выходной сигнал одного элемента (например, сумматора) является входным сигналом другого элемента (например, нелинейного преобразователя). Таким образом, можно проследить, начиная с выходных сигналов сети, от какого элемента сети пришел сигнал к данному элементу.

Стандартный нейрон является типичным участком любой нейронной сети. Поэтому достаточно выяснить, как вычисляются допустимые погрешности для элементов стандартного нейрона. В результате получим возможность вычислить допустимые погрешности для любого участка сети, двигаясь по сети от нейрона к нейрону.

Дальше >>

Нейроинформатика