|
Хотелось бы иметь возможность читать текст сносок при использовании режима "Версия для печати" |
Базисные средства манипулирования реляционными данными: алгебра A Дейта и Дарвена
Введение
Обсуждавшаяся в предыдущей лекции алгебра Кодда в большей степени базируется на теории множеств. Базовыми операциями являются переименование атрибутов, объединение, пересечение, взятие разности, декартово произведение, проекция и ограничение. Операция соединения общего вида, хотя и включается в алгебру, является вторичной и явно представляется через другие операции. Фундаментальная же в реляционном подходе операция естественного соединения выражается через соединение общего вида и в алгебру не включается. В терминах алгебры Кодда проще всего определяются алгебраические черты языка SQL, в частности общая семантика оператора SELECT.
Базисом предложенной Крисом Дейтом и Хью Дарвеном Алгебры A являются операции реляционного отрицания (дополнения), реляционной конъюнкции (или дизъюнкции ) и проекции ( удаления атрибута ). Реляционные аналоги логических операций определяются в терминах отношений на основе обычных теоретико-множественных операций и позволяют выражать напрямую операции пересечения, декартова произведения, естественного соединения, объединения отношений и т. д. Путем комбинирования базовых операций выражаются операции переименования атрибутов, соединения общего вида, взятия разности отношений. Алгебра A позволяет лучше осознать логические основы реляционной модели, хотя, безусловно, является в меньшей степени ориентированной на практическое применение, чем алгебра Кодда1Нельзя не упомянуть еще и о том, что "алгебра" Кодда в действительности не является алгеброй отношений в математическом смысле, поскольку ее операции применимы не ко всем отношениям. В отличие от этого Алгебра A - это "настоящая" алгебра, в которой отсутствуют какие-либо ограничения на операнды операций.. Даже сами авторы Алгебры A, Дейт и Дарвен, в своем учебном языке Tutorial D используют не Алгебру A напрямую, а некоторое ее надмножество, в большей степени напоминающее алгебру Кодда.
Базовые операции Алгебры A
Материал этой лекции излагается на несколько более формальном уровне, чем в предыдущих лекциях. Используемые понятия определяются так же, как и в лекции 2, но для удобства и обеспечения точности изложения мы повторим определения.
Пусть r – отношение, A – имя атрибута отношения r, T – имя соответствующего типа (т. е. типа или домена атрибута A ), v – значение типа T. Тогда:
- заголовком Hr отношения r называется множество атрибутов, т.е. упорядоченных пар вида <A, T>. По определению никакие два атрибута в этом множестве не могут содержать одно и то же имя атрибута A ;
- кортеж tr, соответствующий заголовку Hr, – это множество упорядоченных триплетов вида <A, T, v>, по одному такому триплету для каждого атрибута в Hr ;
- тело Br отношения r – это множество кортежей tr. Заметим, что (в общем случае) могут существовать такие кортежи tr, которые соответствуют Hr, но не входят в Br.
Заметим, что заголовок – это множество (упорядоченных пар вида <A, T> ), тело – это множество (кортежей tr ), и кортеж – это множество (упорядоченных триплетов вида <A, T, v> ). Элемент заголовка – это атрибут (т. е. упорядоченная пара вида <A,T> ); элемент тела – это кортеж; элемент кортежа – это упорядоченный триплет вида <A, T, v>. Любое подмножество заголовка – это заголовок, любое подмножество тела – это тело, и любое подмножество кортежа – это кортеж.
Определим несколько основных операций (как будет показано далее, некоторые из них избыточны). Каждое из последующих определений состоит из: формальной спецификации ограничений (если они имеются), применимых к операндам соответствующей операции; формальной спецификации заголовка результата этой операции; формальной спецификации тела этого результата и неформального обсуждения формальных спецификаций.
Во всех формальных спецификациях exists обозначает квантор существования ; exists tr означает "существует такой tr, что". Символ "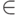 " означает принадлежность элемента множеству;
" означает принадлежность элемента множеству;  означает, что элемент tr принадлежит множеству Br. Выражение
означает, что элемент tr принадлежит множеству Br. Выражение  означает, что элемент tr не принадлежит множеству Br. Операции minus и union являются традиционными теоретико-множественными операциями взятия разности и объединения множеств.
означает, что элемент tr не принадлежит множеству Br. Операции minus и union являются традиционными теоретико-множественными операциями взятия разности и объединения множеств.
Поскольку некоторые базовые операции Алгебры A имеют названия обычных логических операций, чтобы избежать путаницы, имена реляционных операций берутся в угловые скобки: <NOT>, <AND>, <OR> и т. д. В исходный базовый набор операций входят операции реляционного дополнения <NOT>, удаления атрибута <REMOVE>, переименования атрибута <RENAME>, реляционной конъюнкции <AND> и реляционной дизъюнкции <OR>.
