|
Добрый день. Подскажите формулы при решении задачи на рис. 2.2 в лекции №2. Закон Ома, какие должны использоваться формулы для I и R |
Финансист - оптимизатор. Проект "MasterF"
В финансово - хозяйственной деятельности предприятий нередко возникают достаточно сложные задачи, требующие применения оптимизационных математических методов. Excel в совокупности с другими приложениями Office 2000 позволяет решать подобные задачи, обеспечивая пользователя всеми необходимыми средствами поддержки, начиная с постановки задачи и кончая представлением результатов решения. Однако эти средства рассчитаны на весьма продвинутых пользователей с хорошей математической подготовкой. Как правило, чтобы такие средства эффективно применялись на практике, необходима надстройка над Office 2000, сделанная программистами на VBA. Подобные надстройки могут иметь специальную форму, например, быть оформленными в виде AddIns, или могут быть документами Excel, созданными для решения специальной задачи. Подобные надстройки по сложившейся традиции называют "Помощниками" или "Мастерами".
В этой главе я приведу пример построения одного из таких помощников, занимающегося решением оптимизационных задач, возникающих в процессе финансовой деятельности офиса. Помощник, который назовем "MasterF", должен помочь финансисту в решении его задачи на всех этапах, начиная от постановки до получения и анализа результатов решения.
Цель, которую я ставлю перед собой в этой главе, состоит не столько в том, чтобы показать, как решается данная конкретная задача, а на ее примере продемонстрировать возможность Excel по созданию подобных помощников. Тем не менее, начну с задачи, для решения которой и был построен MasterF
Планирование инвестиций с учетом риска
Приведу содержательную постановку задачи, которая была предложена моим коллегой - доцентом экономического факультета - Шукурьяном С. И.
АОЗТ "Риск" заключило контракт на покупку оборудования на общую сумму 750000$. В соответствии с условиями контракта аванс в размере 150000$ необходимо заплатить через 2 месяца, а оставшуюся сумму через 6 месяцев после заключения контракта. Для обеспечения выплат руководитель "Риска" создал временный целевой фонд и назначил его руководителя. Начальный капитал фонда составляет сумму, меньшую, чем та, которую предстояло заплатить в конце контракта. Остальные деньги руководитель фонда должен был обеспечить за счет грамотной инвестиционной политики и получения соответствующих дивидендов. Кроме того, руководитель "Риска" поставил жесткие ограничения на среднюю величину допустимого ежемесячного риска и среднюю ежемесячную длительность вложения денег. Задать величину требуемого начального капитала должен был руководитель фонда, но, естественно, руководство хотело, как можно меньше денег вложить в начальный капитал фонда.
Руководитель фонда после предварительных консультаций с экспертами отобрал 4 возможных проекта, которые разумно было инвестировать. И хотя число инвестиционных проектов сравнительно невелико, подобрать наилучшее или даже просто приемлемое решение "вручную" оказалось совсем не просто. И тогда руководитель фонда обратился к программистам с целью помочь ему в решении задачи. Так появился помощник MasterF.
Программист начал с формализации постановки задачи, стараясь сделать ее на начальном этапе как можно более простой. Начнем с инвестиционных проектов. Каждый из них имеет следующие характеристики:
- Дату начала и длительность.
- Число этапов, на каждом из которых производится выплата денег. Для этапа указана его длительность и сумма, выплачиваемая в конце этапа.
- Минимальная и максимальная сумма, которую можно вложить в проект.
- Степень риска проекта, заданная независимыми экспертами.
Данные о четырех отобранных инвестиционных проектах представлены в таблице:
| Названия проектов | Месяцы | Риски | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| A | 1.015 | 1.015 | 1.015 | 1.015 | 1.015 | 1.015 | 1 |
| B | 1.035 | 1.035 | 1.035 | 4 | |||
| C | 1.06 | 1.06 | 9 | ||||
| D | 1.11 | 7 | |||||
Как следует из этой таблицы, проект B, например, состоит из трех этапов, длительность каждого - 2 месяца. В конце этапа прибыль составляет 3,5% от суммы, вложенной на начало этапа. Аналогичный смысл имеют данные и для других проектов. Никаких ограничений на суммы, вкладываемые в проекты, в данном случае не накладывается. Последний столбец таблицы задает риски каждого проекта.
Формальная постановка задачи
Введем обозначения:
- n - число этапов, на которых принимаются решения о вложении денег в тот или иной проект. В нашем примере такие решения принимаются каждый месяц и потому n= 6.
- m - число проектов. В примере m =4.
- Pi - проекты, где i = 1 …m.
- Ri - величина риска проекта Pi.
- qi - число этапов проекта Pi.
- Si j - сумма денег, вкладываемая в проект Pi на j -м этапе. Si j - это и есть наши искомые переменные, значения которых предстоит найти в ходе решения задачи. Заметьте, что здесь i = 1 ... m, j = 1 ... qi
-
N - общее число искомых переменных, которое определяется формулой

- K - первоначальный капитал фонда.
- Rc - допустимый средний риск.
- Tc -допустимая средняя длительность проекта.
Перейдем теперь к формулировке оптимизационной задачи:
Необходимо минимизировать первоначальный капитал фонда
K => min
при выполнении четырех групп ограничений:
Ограничения баланса: Bi = 0 i = 1…n
Ограничения среднего риска: Ri <= Rc i = 1…n
Ограничения средней длительности проекта: Ti <= Tc i = 1…n
Ограничения на положительность значений: Si j >= 0 i = 1 ... n, j = 1 ... qi
Первую группу ограничений составляют ежемесячные ограничения баланса. Все имеющиеся к началу месяца сбережения следует вложить в те или иные проекты. Деньги " в чулке" хранить нельзя. Поэтому сумма денег, полученных в конце месяца с учетом дивидендов и выплаты долговых обязательств, равна сумме денег, вкладываемых в инвестиционные проекты на следующем месяце. Конечно, чтобы такая возможность всегда существовала, необходимо, чтобы среди проектов был "безопасный" проект с наименьшим риском и минимальным сроком вложения. Параметры такого проекта должны быть заведомо меньше задаваемых значений среднего риска и средней продолжительности. Существование такого проекта гарантирует существование решения задачи для любых исходных данных. В нашем примере это первый проект. Понятно, что таким проектом может считаться вложение денег в Сбербанк.
Отметим еще краевые балансовые ограничения. В начале первого месяца сумма вложений в инвестиционные проекты равна начальному капиталу фонда. В конце последнего месяца сумма полученных денег равна сумме, которую следует выплатить для погашения долга. Эти ограничения вытекают из предназначения временного целевого фонда.
Я не стану выписывать балансовые ограничения в явном виде, поскольку, с одной стороны, они достаточно понятны, с другой стороны их формальная запись для общего случая довольно громоздка из-за динамического характера решаемой задачи. Ограничусь тем, что приведу краевые уравнения баланса и уравнение для одного из месяцев. Вот как выглядит уравнение баланса на начальном этапе:
K = S1 1 + S2 1 + S3 1 + S4 1
Это уравнение задает целевую функцию - начальный капитал K, значение которого предстоит определить. Уравнение баланса говорит о том, что весь начальный капитал должен быть вложен в инвестиционные проекты.
Баланс по завершении работы фонда имеет вид:
1.015* S1 6 + 1.035* S2 3 + 1.06* S3 2 + 1.11* S4 1 = Capital
Это уравнение говорит, что деньги, полученные в конце шестого месяца от всех проектов, должны давать сумму, равную требуемому капиталу.
Баланс после истечения двух месяцев с учетом выплаты аванса имеет вид:
1.015* S1 2 + 1.035* S2 1 - D1 = S1 3 + S2 2
Вторую группу составляют ежемесячные ограничения среднего риска. Если обозначить через Li k сумму инвестиций i -го проекта в k - м месяце, то эти ограничения в общем случае имеют вид:
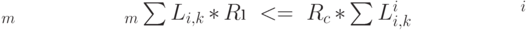
Исходя из этой общей формулы, можно выписать ограничения этой группы в конкретной ситуации. Приведу только одно ограничение для четвертого месяца нашего примера:
R1* S1 4 + R2* S2 2 + R3* S3 2 + R4* S4 1 <= Rc*(S1 4 + S2 2 + S3 2 + S4 1)
Третью группу составляют ежемесячные ограничения средней длительности проектов. Общая формула имеет вид:
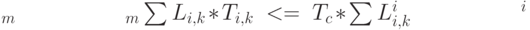
В построении ограничений участвует опять таки средневзвешенная, но теперь уже с учетом длительности проектов сумма инвестиций i -го проекта в k - м месяце. Формулы становятся чуть более сложными, поскольку в текущем месяце используются не постоянные коэффициенты, как в случае с подсчетом рисков, а динамически пересчитываемые коэффициенты, задающие время до окончания этапа проекта. Опять таки, ограничимся тем, что приведем только одно ограничение для того же четвертого месяца нашего примера:
T1 4* S1 4 + T2 4* S2 2 + T3 4* S3 2 + T4 4* S4 1 <= Tc*(S1 4 + S2 2 + S3 2 + S4 1)
В нашем примере: T1 4 = 1; T2 4 =1; T3 4 = 3; T4 4 = 3.
С точки зрения математика полученная задача является довольно простой задачей линейного программирования. Ее решение может быть получено в Excel вручную, используя возможности мощного инструментального средства, встроенного в Excel, - решателя Solver. Однако понятно, что даже опытный пользователь, вряд ли сумеет без ошибок выписать все ограничения задачи, особенно при увеличении числа инвестиционных проектов.
