|
Добрый день. Подскажите формулы при решении задачи на рис. 2.2 в лекции №2. Закон Ома, какие должны использоваться формулы для I и R |
Начала программирования в Excel
Задача 4
Найти корень уравнения F(x)=0 , где функция F(x) задается программистом и реализована на VBA.
Можно ли сочетать программирование без программирования с "настоящим" программированием. Ответ - безусловно "да". Данный пример позволяет продемонстрировать эту возможность. Я покажу, что функцию, корень которой разыскивается, и ее производную можно написать на VBA. При вызове этих функций в формулах рабочего листа в качестве параметров им можно передавать ячейки таблицы, записанные как в абсолютных, так и в относительных адресах. Копирование таких формул производит прежний эффект. Решение задачи 4 обобщает решение задачи 3, распространяя его на те ситуации, когда функция, корень которой разыскивается, не может быть задана простой формулой, и ее нельзя описать с помощью формул рабочего листа. Такая ситуация достаточно типична, например, когда требуются циклические вычисления для получения значения функции. Все эти трудности снимаются, благодаря тому, что Excel позволяет вызывать в формулах рабочего листа функции, написанные на VBA . В качестве примера функции F(x) я буду использовать ту же функцию, что и в задаче 3, - полином 4-й степени. Это позволит нам сравнить два решения и убедиться в том, что решение, полученное с использованием программирования, выглядит даже более элегантно, я бы сказал. С другой стороны, заметьте, сохраняются все преимущества, которые дает машина вычислений Excel, не требующая программирования. Обратите внимание, пример демонстрирует передачу данных из рабочего листа в функцию, написанную на VBA и обратно.
Для решения задачи 4 я написал на VBA две функции. Вот как они выглядят:
Public Function Polinom4(Cofs As Variant, X As Variant) As Variant 'Вычисляет значение полинома 4-й степени в точке, 'заданной параметром X. 'Коэффициенты полинома передаются в первом параметре Cofs. 'Значением параметра Cofs может быть объект Range. Polinom4 = (((Cofs.Cells(1) * X + Cofs.Cells(2)) * X + _ Cofs.Cells(3)) * X + Cofs.Cells(4)) * X + Cofs.Cells(5) End Function Public Function Pr4(Cofs As Variant, X As Variant) As Variant 'Вычисляет значение производной полинома 4-й степени в точке, 'заданной параметром X. 'Коэффициенты полинома передаются в первом параметре Cofs. 'Значением параметра Cofs может быть объект Range. Pr4 = ((4 * Cofs.Cells(1) * X + 3 * Cofs.Cells(2)) * X + _ 2 * Cofs.Cells(3)) * X + Cofs.Cells(4) End Function
Затем я практически повторил действия, предпринятые для решения задачи 3. Реально, конечно, я ничего не повторял, а просто создал копию листа 4 и внес в нее необходимые изменения. Эти изменения коснулись тех ячеек, в которых вычисляется значение функции и ее производной. В ячейке B12 я заменил формулу, вычисляющую функцию, на вызов функции Polinom4:
"=Polinom4($C$9 : $G$9; A12)"
Аналогично в ячейке B26 появилась формула:
"=Polinom4($C$9 : $G$9; A26)"
а в ячейке C26:
"=Pr4($C$9 : $G$9; A26)"
Обратите внимание, я передаю вызываемым функциям объект Range в качестве первого параметра, в котором записаны значения коэффициентов полинома. В качестве второго параметра также передается объект Range, но определяющий уже единственную ячейку. Заметьте, при передаче первого параметра я использовал абсолютные имена, поскольку коэффициенты полинома находятся в строго фиксированных ячейках и их адреса не должны меняться при копировании формулы. Для второго параметра использован относительный адрес, поэтому он должным образом будет меняться при копировании формул.
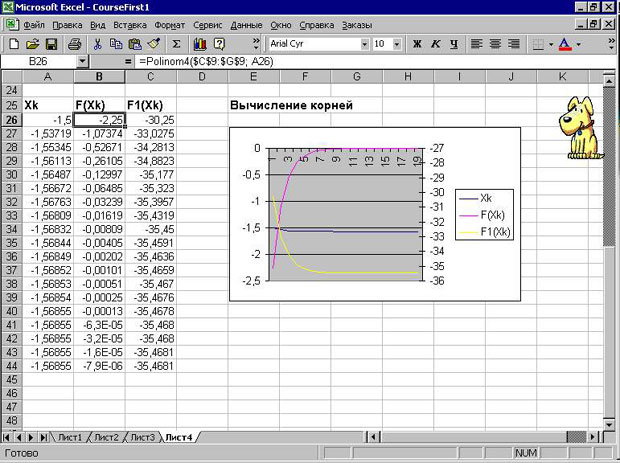
Наш пример интересен и тем, что в нем показано, как передается массив ячеек и отдельная ячейка рабочего листа в функцию VBA. С другой стороны, результат вычисления функции передается в формулу рабочего листа. Заметьте, что хотя формальный параметр функций имеет тип Variant, ему можно в качестве фактического параметра передавать объекты Range. В теле функции можно работать с этим параметром, как с объектом Range, вызывая его свойства и методы, как это делается в наших функциях, где вызывается свойство Cells этого объекта. Я еще вернусь в последующем к теме передачи информации между рабочим листом и процедурами и функциями VBA и остановлюсь на этом более подробно. В заключение, взгляните, как выглядит решение этой задачи. Поскольку ищутся корни той же функции, что и в задаче 3, то, чтобы избежать повторения рисунков, я привожу решение, в котором найден другой корень нашей функции:
Массивы, формулы с массивами
В предыдущем примере возникла необходимость передать массив ячеек в функцию, написанную на VBA. Сейчас же я хочу рассмотреть несколько примеров, демонстрирующих возможности работы с массивами непосредственно на рабочем листе без использования программирования.
Создание одномерных массивов (векторов) и двумерных (матриц) на рабочем листе Excel вручную представляется совершенно естественным делом и вряд ли стоит, что-либо говорить по этому поводу, - берешь и создаешь. Также просто при желании дать имена этим массивам. Программно это можно сделать, используя свойство Name объекта Range. Вручную это можно делать по-разному, выделив объект Range и задав его имя в окошке имен или использовать для этой цели диалоговое окно, до которого можно добраться из меню Вставка | Имя.
Но что можно сделать с массивами при "ручной работе"? Какие операции допустимы над массивами при работе с рабочим листом. На самом деле сделать можно немного, но кое-что сделать удается. Для этой цели в Excel можно использовать формулы, аргументами которых, а возможно и результатом являются массивы. Такие формулы называются " формулами с массивами ", " формулами над массивами ", а иногда еще проще - " массивными формулами ".
Если результатом такой формулы является скаляр (одно значение), то такая формула вводится, как обычно, в ячейку, в которой и будет находиться результат вычислений. Единственное, но важное отличие состоит в том, завершить ввод формулы над массивами следует нажатием комбинации клавиш: "Ctrl+ Shift + Enter". Это немедленно отобразится в поле ввода формулы тем, что такая формула будет заключена в фигурные скобки. Заметьте, что нельзя самому задать эти скобки для придания формуле статуса "массивной". Формулу следует всегда начинать со знака равенства, а не с фигурной скобки.
Если результатом формулы является массив, то предварительно этот массив должен быть выделен и затем уже следует ввести формулу над массивом, она как бы распределяется на все элементы выделенного массива. Заметьте, что при работе с формулами над массивами есть существенное ограничение - аргументы и результат должны быть, как правило, массивами одинаковой размерности и, более того, вытянуты в одном и том же направлении. Не может быть аргумент строка, а результат столбец. Именно это ограничение существенно снижает возможности работы с матрицами вручную. Давайте перейдем к примерам, на которых легче понять некоторые детали, а также семантику, задающую детали реализации формул с массивами.
Задача 5
Вычислить скалярное произведение двух векторов c = AB = Sum(Ai*Bi)
В первом варианте решения этой задачи я на рабочем листе "Лист5" нашей книги CourseFirst создал два вектора A и B, введя значения их компонент соответственно в ячейки D2:F2 и D3:F3. Для получения скалярного произведения этих векторов я написал формулу над массивами: " {=СУММ(D2:F2*D3:F3)} ". Поскольку результатом вычислений является в данном случае скаляр, то формула помещается в единственную ячейку. Я выбрал для результата ячейку D4.
Второй вариант решения задачи отличается лишь тем, что векторам A и B даны имена. Свои действия в этом варианте опишу более подробно:
- Ввел компоненты вектора A в ячейки D6:F6.
- Выделил эту область и в окне имен дал вектору (объекту Range ) имя VectorA
- Аналогично ввел компоненты вектора B в ячейки D7:F7 и вектору дал имя VectorB.
- В ячейку D8 ввел формулу над массивами: " {=СУММ(VectorA*VectorB)} ".
- Получил ожидаемый результат.
Задача 6
Вычислить вектор, компоненты которого являются произведением соответствующих компонент векторов A и B
C =A*B ={A1*B1, A2*B2, … An*Bn}К сожалению, формулы над массивами не позволяют вычислить настоящее векторное произведение. Эту задачу вообще невозможно решить без программирования. Поэтому я ограничился менее интересной, но зато более простой задачей, главная цель которой продемонстрировать формулу над массивами результат которой также является массивом.
В качестве сомножителей я использовал VectorA и VectorB предыдущей задачи. Но поскольку теперь результатом является вектор той же размерности, что и аргументы, то я выделил область ячеек для этого вектора - D12:F12 и ввел формулу над массивами:
"{= VectorA * VectorB }".В результате был получен массив VectorC, представляющий произведение векторов A и B. Так что заметьте, произведением векторов одинаковой размерности, полученным в результате обычной операции умножения, является вектор, каждая координата которого задается произведением соответствующих координат векторов сомножителей. Чуть дальше я уточню эту формулировку и расскажу более подробно о выполнении операций над векторами.