Основы ортогонального доступа с частотным разделением каналов (OFDMA).
Регулирование мощности
В теории, лучшая стратегия регулирования мощности с точки зрения пропускной способности - так называемая стратегия "заполнения водой" (Waterfilling)., в которой больше мощности распределяется сильным каналам, и меньше количеству мощности, распределяется слабым каналам [ 95 ] . Хотя на практике в некоторых случаях истина может быть противоположна. Например, рассматривая к рис. 8.13 можно установить, что нет никакой разницы в производительности при отношении входной сигнал – шум 11 и 13 децибел в обоих случаях производительность - 3 бита в сек/Гц. Поэтому, если SNR улучшился с 11 децибелов до 13 децибелов, хорошо бы сообщить передатчику, чтобы он понизил мощность передачи, чтобы сохранить мощность и создавать меньше помех соседним ячейкам [ 81 ] .
таблица 8.6показывает скорости передачи данных при различных видах модуляции и кодирования для каналов на 5 и 10 МГЦ с PUSC подканалами. Продолжительность кадра - 5 миллисекунд. Каждый кадр имеет 48 OFDM символов. Из них 44 OFDM символа, предназначены для передачи данных. Выделенные значения - это скорости данных для необязательного способа модуляции 64QAM в направлении вверх (UL).
CTC –Convolution Turbo Code - Сверточный Турбокод
Методы распределения ресурсов для OFDMA
Есть множество различных способов использовать в своих интересах мультипользовательское разнесение и адаптивную модуляцию в системах OFDMA. Алгоритмы, которые обеспечивают такие преимущества, не определены стандартами, и каждый разработчик имеет право применить собственные инновационные процедуры.
Идея разработки таких алгоритмов состоит в том, чтобы определить на время соединения (сеанса) порядок, назначения пользователям поднесущих частот, и для каждого пользователя на каждой поднесущей частоте определить соответствующую мощность. Ниже, мы дадим краткий обзор некоторых возможных подходов к распределению ресурса.
Распределение ресурса обычно решается, как одна из двух возможных проблем:
- Проблема оптимизации с ограничением, или более конкретно -процедура минимизации полной мощности передачи с ограничением на пользовательскую скорость передачи данных [ 68 ] , [ 94 ] или
- Проблема максимизации скорости передачи данных с ограничением на полную мощность передачи [ 67 ] , [ 71 ] , [ 72 ] , [ 95 ] .
Первая цель соответствует приложениям с фиксированной скоростью (например, речь), в то время как вторая больше соответствует приложениям, имеющим пики, таким как данные или другим IP приложениям.
Алгоритм максимальной суммы скоростей.
Цель алгоритма максимальной суммы скоростей (MSR - maximum sum rate), как указывает название, максимизировать сумму скоростей всех пользователей, с учетом ограничения полной мощности передачи [ 95 ] .
Этот алгоритм оптимален, его цель состоит в том, чтобы передать через систему получить насколько возможно большее количество данных в заданный промежуток времени. Недостаток MSR - это то, что при таком алгоритме весьма вероятно, что нескольким пользователям, которые находятся близко к базовой станции (и, следовательно, имеют превосходные каналы), будут распределены все системные ресурсы.
Теперь кратко охарактеризуем 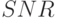 , скорость данных, мощность, и распределение поднесущих частот, который можно получить, используя
, скорость данных, мощность, и распределение поднесущих частот, который можно получить, используя 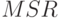 алгоритм. Пусть
алгоритм. Пусть  обозначает мощность передачи пользователя
обозначает мощность передачи пользователя  на поднесущей частоте
на поднесущей частоте  . Отношение "входного сигнала к шуму" для пользователя
. Отношение "входного сигнала к шуму" для пользователя  на поднесущей частоте
на поднесущей частоте  , обозначим
, обозначим  . Эта величина может быть выражена как:
. Эта величина может быть выражена как:
 |
( 8.3) |
Используя формулу пропускной способности Шеннона 6В этой секции, мы будем использовать формулу пропускной способности Шеннона как меру производительности. Практически, есть промежуток между достигнутой скоростью данных и максимумом (согласно Шеннона) скорости, которая может быть просто охарактеризована с промежутком SNR нескольких децибелов. Поэтому этот подход к распределению ресурса правилен, но точные числа, здесь являются оптимистическими для измерения производительности, MSR алгоритм максимизирует следующую величину:
 |
( 8.4) |
с ограничением полной мощности
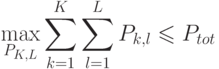 |
( 8.5) |
Пропускная способность суммы максимальна, если полная производительность в каждой поднесущей частоте максимальна. Следовательно, проблема оптимизации пропускной способности максимальной суммы может быть разделена на  более простых проблем. Максимальности каждой поднесущей для каждой частоты. Далее, пропускная способность суммы в поднесущей частоте
более простых проблем. Максимальности каждой поднесущей для каждой частоты. Далее, пропускная способность суммы в поднесущей частоте  , обозначенная как
, обозначенная как 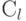 , может быть записан как
, может быть записан как
 |
( 8.6) |
где
-
 обозначает интерференцию других пользователей к пользователю
обозначает интерференцию других пользователей к пользователю  с поднесущей частотой
с поднесущей частотой  ,
, -
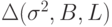 - мощность внешних щумов.
- мощность внешних щумов.
 , максимимальна, когда вся доступная мощность
, максимимальна, когда вся доступная мощность  отдается только единственному пользователю с наибольшим усилением канала на поднесущей частоте
отдается только единственному пользователю с наибольшим усилением канала на поднесущей частоте  Этот результат согласуется с интуицией: если каждый канал отдать пользователю с лучшим усилением в этом канале, то общая сумма мощностей будет максимизирована. Этот метод называют иногда - "жадная" оптимизация. Сумма полной пропускной способности может быть определена, сложением скоростей на каждой поднесущей частоте.
Этот результат согласуется с интуицией: если каждый канал отдать пользователю с лучшим усилением в этом канале, то общая сумма мощностей будет максимизирована. Этот метод называют иногда - "жадная" оптимизация. Сумма полной пропускной способности может быть определена, сложением скоростей на каждой поднесущей частоте.
Алгоритм Максимальной Справедливости
Хотя при использовании алгоритма MSR полная производительность получается максимальной, однако в сотовой системе, где потери на затухание изменяются в соответствии с последовательностью обслуживания пользователей, при применении алгоритма MSR некоторые пользователи будут чрезвычайно плохо обслужены. Альтернативная замена алгоритму MSR, алгоритм максимальной справедливости (FA - fairness algorithm) [ 47 ] , [ 82 ] , [ 93 ] распределяет поднесущие частоты и мощность так, чтобы скорость данных передаваемая минимальным пользователем была максимальна. Это, по существу, соответствует выравниванию скоростей данных всех пользователей.
Алгоритм максимальной справедливости может иногда называться как проблема МиниМакса (Max-Min), так как цель состоит в том, чтобы максимизировать минимальную скорость данных.
Оптимизация условий для поднесущей частоты при методе мини - макса и распределение мощности значительно более трудно определить чем в случае MSR, потому что невозможно построить объективная функцию "минимальности пользователя". Найти одновременно оптимальную поднесущую частоту и распределение мощности - это проблема особой трудности – неразрешимая проблема (NP - проблема) Поэтому, ставится задача более низкой сложности, найти почти оптимальные алгоритмы, в которые оптимизируют поднесущие частоты и распределение мощности отдельно.
Общий подход состоит в том, чтобы принять первоначально равную мощность для каждой распределенной поднесущей частоты, и затем многократно назначать каждую доступную поднесущую частоту для пользователя низкой скорости и с лучшим каналом для этой скорости. Таким образом каждый новый пользователь выбирает поднесущие, наилучшие для него на данный момент. Такой алгоритм иногда называют "жадным алгоритмом"
Пропорциональный Алгоритм Ограничений Скорости
Слабость алгоритма максимальной справедливости это то, что распределение скорости среди пользователей не гибкое. Полная производительность в значительной степени ограничена пользователем с худшим SNR так, как большинство ресурсов будет распределено в среднем, т.е. для пользователей с лучшими условиями качество будет искусственно занижено, а с худшими условиями это качество все равно может быть недостаточно.
В беспроводной широкополосной сети, весьма вероятно, что различные пользователи, требуют, чтобы можно было существенно менять скорости передачи в зависимости от прикладных задач.
Обобщение Максимального алгоритма Справедливости - алгоритм Пропорционального Ограничения Скорости (PRC Proportional Rate Constraints)
[
87
]
. Цель алгоритма состоит в том, чтобы максимизировать производительность суммы, с дополнительным ограничением, что, скорость данных каждого пользователя пропорциональна набору заранее заданных системных параметров (весовых коэффициентов) 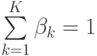 . Математически, пропорциональное ограничение скорости передачи данных может быть выражено как:
. Математически, пропорциональное ограничение скорости передачи данных может быть выражено как:
 |
( 8.7) |
где 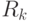 достигнутая скорость передачи данных каждого пользователя
достигнутая скорость передачи данных каждого пользователя 
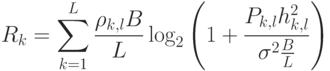 |
( 8.8) |
и 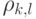 может принимать значение либо
может принимать значение либо  либо
либо  , указывая, используется ли поднесущая частота
, указывая, используется ли поднесущая частота  пользователем
пользователем  или нет.
или нет.
При алгоритме Максимальной Справедливости все 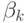 равны. Преимущества рассматриваемого метода это то, что любые произвольные скорости передачи данных можно получить, изменяя значения
равны. Преимущества рассматриваемого метода это то, что любые произвольные скорости передачи данных можно получить, изменяя значения 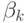 .
.
Задачу оптимизации с применением алгоритма Пропорционального Ограничения Скорости (PRC) очень трудно решить непосредственно, так как это включает одновременное рассмотрение непрерывных переменные 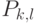 и двоичных переменных
и двоичных переменных 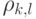 . Такая функция не обладает свойством выпуклости и плохо оптимизируется формальными методами. Что касается случая Максимального Справедливости, благоразумный подход состоит в том, чтобы отделить поднесущую частоту и распределение мощности, и соглашаться на почти оптимальную поднесущую частоту, и распределение мощности который может быть достигнуто с управляемой сложностью. Почти оптимальный подход был получен в
[
83
]
,
[
88
]
.
. Такая функция не обладает свойством выпуклости и плохо оптимизируется формальными методами. Что касается случая Максимального Справедливости, благоразумный подход состоит в том, чтобы отделить поднесущую частоту и распределение мощности, и соглашаться на почти оптимальную поднесущую частоту, и распределение мощности который может быть достигнуто с управляемой сложностью. Почти оптимальный подход был получен в
[
83
]
,
[
88
]
.
Пропорциональное Справедливое Планирование
До сих пор мы обсудили три алгоритма, при которых делается попытка попытку мгновенно достигнуть целей - таких как полная сумма, производительность (MSR алгоритм), максимальная справедливость (равные скорости данных для всех пользователей), или задать пропорциональные скорости для каждого пользователя.
Альтернативой этому может быть попытка достигнуть таких целей через какое-то время, что обеспечивает существенную дополнительную гибкость к алгоритмам планирования. В этом случае, в дополнение к показателям - производительность и справедливость, вводится третий параметр - время задержки. Эта величина показывает, какое время можно ждать до предоставления оптимального канала пользователю. Если время задержки приемлемо то, планировщик может просто подождать, когда параметры его канала были оптимальны. Фактически, MSR алгоритм достигает и справедливости и максимальной производительности, если можно предположить, что нет ограничений на время задержки. Тогда пользователи в долгосрочной перспективе (порядка минут, часов, или больше) будут иметь в среднем нужные по качеству каналы. В этом случае можно найти алгоритмы, которые соблюдают равновесие между временем задержки и производительностью. Заметим, что это и может быть справедливо для времен порядка секунд. Наиболее популяр ный алгоритм - Пропорционального Справедливого Планирования (PF - Proportional Fairness). Этот PF планировщик разработан так, чтобы использовать в своих интересах мультипользовательское разнесение, с поддержанием долгосрочной производительности для всех пользователей.
Пусть 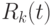 , обозначает мгновенную скорость данных, которую пользователь
, обозначает мгновенную скорость данных, которую пользователь  может достигнуть за время
может достигнуть за время  , а
, а 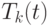 -средняя производительность для пользователя
-средняя производительность для пользователя  и
и  - слот времени. Пропорциональный планировщик справедливости выбирает для передачи пользователя, обозначенного как
- слот времени. Пропорциональный планировщик справедливости выбирает для передачи пользователя, обозначенного как  , с самым высоким
, с самым высоким  . Это эквивалентно тому, что пользователь выбирает, через некоторое время (задержка) несущие с самой высокой мгновенной скоростью относительно средней скорости. Средняя производительность
. Это эквивалентно тому, что пользователь выбирает, через некоторое время (задержка) несущие с самой высокой мгновенной скоростью относительно средней скорости. Средняя производительность 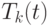 для всех пользователей тогда получается согласно:
для всех пользователей тогда получается согласно:
 |
( 8.9) |
Так как пропорциональный планировщик справедливости выбирает пользователя с наибольшей мгновенной скоростью передачи данных относительно средней производительности, то вряд ли может быть выбран "плохой" канал для каждого пользователя.
С другой стороны, пользователи который были обслужены с недостаточным качеством последовательно, получают приоритет при планировании, который и способствует справедливости. Параметр 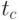 управляет временем задержки системы. Если
управляет временем задержки системы. Если 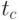 большое, то время задержки увеличивается для нахождения более высокой суммы производительности. Если
большое, то время задержки увеличивается для нахождения более высокой суммы производительности. Если 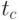 маленькое, время задержки уменьшается, так как математическое ожидание производительности изменяется более быстро, за счет самой производительности.
маленькое, время задержки уменьшается, так как математическое ожидание производительности изменяется более быстро, за счет самой производительности.
Пропорциональный планировщик справедливости был широко принят в пакетных системах передачи данных, таких как HSDPA и 1xEV-DO, где 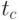 обычно устанавливается между 10 и 20.
обычно устанавливается между 10 и 20.
Одно интересное свойство PF планирования эта то, что при  , сумма логарифмов пользовательских скоростей данных стремится к максимуму. То есть PF планирование приводит к максимуму
, сумма логарифмов пользовательских скоростей данных стремится к максимуму. То есть PF планирование приводит к максимуму
 |
( 8.10) |
Хотя пропорциональный планировщик справедливости был первоначально разработан только для систем с временными слотами, он может быть приспособлен к OFDMA системе.
В системе OFDMA, из-за множества параллельных поднесущих частот в частотной области, пользователи могут работать на различных поднесущих частотах одновременно. Первоначальный PF алгоритм может быть расширен на OFDMA, если обрабатывать каждую поднесущую частоту независимо.
Пусть  , приемлемая скорость данных для пользователя
, приемлемая скорость данных для пользователя  на поднесущей частоте n во временном слоте
на поднесущей частоте n во временном слоте  . Тогда для каждой поднесущей частоты, будет выбран для передачи пользователь с наибольшим
. Тогда для каждой поднесущей частоты, будет выбран для передачи пользователь с наибольшим  . Пусть
. Пусть  , обозначает набор поднесущих частот, которые намечен для пользователя
, обозначает набор поднесущих частот, которые намечен для пользователя  при работе в слоте времени
при работе в слоте времени  , тогда средняя пользовательская производительность получается как:
, тогда средняя пользовательская производительность получается как:
 |
( 8.11) |
Конечно возможны и другая взвешивающие функции планирования PF OFDMA.
Сравнение Рабочих характеристик
В этой секции, мы кратко сравним рабочие характеристики различных алгоритмов планирования для OFDMA, которые, мы обсуждали, чтобы определить их преимущества и достоинства.
Алгоритм максимальной производительности. Сначала, мы рассмотрим выигрыш от много пользовательского разнесения для различных типов алгоритмов.
рис.
8.14 показывает пропускную способность (нормализованную к полной ширине полосы частот) для статического (циклического) TDMA, для алгоритмов пропорциональной справедливости, и максимальной суммы скоростей (MSR). Как и ожидалось, алгоритм MSR достигает лучшей полной производительности, и увеличения усиления по мере увеличения числа пользователей (пропорционально  ). Статический TDMA не дает никакого мультипользовательского усиления, так как пользователи передают информацию независимо от реализации канала. Может быть замечено, что пропорциональный алгоритм справедливости приближается к производительности алгоритма MSR, с потерями на ожидание для не полностью обслуженных пользователей.
). Статический TDMA не дает никакого мультипользовательского усиления, так как пользователи передают информацию независимо от реализации канала. Может быть замечено, что пропорциональный алгоритм справедливости приближается к производительности алгоритма MSR, с потерями на ожидание для не полностью обслуженных пользователей.
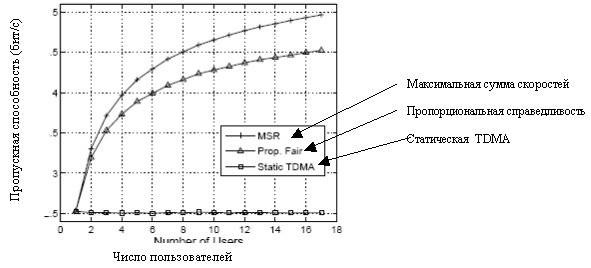
Рис. 8.14. Суммарная произоводительность в зависимости от числа абонентов, для системы из одной несущей частоты (планирование только в одной временной области)
Алгоритм справедливости. Алгоритм Максимальный Справедливости добивается лучших рабочих характеристик для пользователей находящихся в плохих условиях, с небольшим выигрышем в среднем по мощности. Для малого числа абонентов (предельный случай 1) распределение мощности оптимально. Дальнейшее увеличение абонентов приводит к уменьшению средней производительности, поскольку идет достижение относительно равного распределения мощности.
Алгоритм MSR с ожиданием в худшем случае сказывается на нескольких пользователях, которые не получают никаких ресурсов в течение существенного периода времени (потери по времени).
Рассмотрим однородную сеть с 8 пользователями. Первый пользователь имеет средний SNR - 20 децибелов, второй пользователь имеет средний SNR -10 децибелов, и пользователи 3-8 имеют средние SNR 0 децибелов. Это – типовой сценарий, в котором пользователь 1 находится близко к базовой станции, пользователи 3-8 – возле границы соты, и пользователь 2 – между ними. Ясно, большая часть ресурсов будет распределена MSR алгоритмом пользователям 1 и 2.
Плохая сторона этого подхода, конечно, та, что пользователи 3-8 получают производительность приблизительно около нуля. Более сбалансированный подход состоял бы в том, чтобы использовать пропорциональный алгоритм ограничений скорости (PRC - Proportional Rate Constraint) и принять пропорциональные ограничения скоростей, в соответствии с SNR, то есть  . Это позволяет не полностью обслуживаемым пользователям получать по крайней мере некоторую производительность, при сохранении большой части мультипользовательских выигрышей от разнесения. Естественно, более равное назначение
. Это позволяет не полностью обслуживаемым пользователям получать по крайней мере некоторую производительность, при сохранении большой части мультипользовательских выигрышей от разнесения. Естественно, более равное назначение 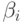 -ым пользователям увеличит справедливость, в крайним случаем при равенстве всех коэффициентов
-ым пользователям увеличит справедливость, в крайним случаем при равенстве всех коэффициентов 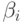 можно уравнять скорости данных для всех пользователей.
можно уравнять скорости данных для всех пользователей.
Итоги Сравнения. таблица 8.8 сравнивает четыре алгоритма распределения ресурса, которые рассматривались в этой главе для OFDMA систем. В итоге, Максимальное распределение Скорости Суммы - лучшее в части полной производительности, имеет низкую вычислительную сложность, но дает очень несправедливое распределение скоростей.
| Алгоритм | Суммарная производительность | Справделивость | Сложность |
|---|---|---|---|
| Максимальная сума скоростей | лучшая | Достаточная и неизменяемая | Низкая |
| Максимальная справедливость | Достаточная | Лучшая , но неизменяемая | Средняя |
| Пропорциональное ограничение скорости | Хорошая | Во многом гибкая | Высокая |
| Пропорциональная справедливость | Хорошая | Гибкая | Низкая |







