|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Измерение нагрузки
Пример 15.3.1: Точность измерения
Отметим, что мы всегда получаем корректную среднюю величину интенсивности нагрузки (15.8). Дисперсия, однако, пропорциональна коэффициенту формы  . Для некоторых случаев распределений времени пребывания в системе мы получаем следующую дисперсию, измеренную с помощью интенсивности нагрузки:
. Для некоторых случаев распределений времени пребывания в системе мы получаем следующую дисперсию, измеренную с помощью интенсивности нагрузки:
Постоянное распределение:

Экспоненциальное распределение:

Наблюдаемое распределение (рис.4.3):

Часто при наблюдении за телефонной нагрузкой мы встречаем случаи, когда  существенно больше, чем 2 (экспоненциальное распределение). Это значение предполагается характерным во многих задачах классического телетрафика (рис.4.3). Поэтому точность измерения всегда ниже, чем данная во многих таблицах. С другой стороны, это компенсируется предположением, что рассматриваемые системы являются не блокирующими. В системе с блокировкой дисперсия становится меньшей из-за отрицательной корреляции между временами пребывания в системе и числом вызовов.
существенно больше, чем 2 (экспоненциальное распределение). Это значение предполагается характерным во многих задачах классического телетрафика (рис.4.3). Поэтому точность измерения всегда ниже, чем данная во многих таблицах. С другой стороны, это компенсируется предположением, что рассматриваемые системы являются не блокирующими. В системе с блокировкой дисперсия становится меньшей из-за отрицательной корреляции между временами пребывания в системе и числом вызовов.
Пример 15.3.2: Относительная точность измерения
Относительная точность измерения дается отношением:
 Коэффициент вариации.
Коэффициент вариации.
Из этого можно заметить, что, если 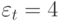 , то мы должны провести удвоение периода измерения, чтобы получить такую же надежность измерения, как и для случая экспоненциально распределенного времени пребывания в системе.
, то мы должны провести удвоение периода измерения, чтобы получить такую же надежность измерения, как и для случая экспоненциально распределенного времени пребывания в системе.
Для данного периода времени мы замечаем, что точность измерения интенсивности нагрузки в маленькой группе пучков каналов является намного большей, чем при измерении в большой группе пучков каналов, потому что точность зависит только от интенсивности нагрузки А. Ошибка в оценке нагрузки на 10 % при измерении маленькой группы пучка каналов намного меньше влияет на точность измерения, чем тот же самый процент ошибки в большой группе пучков каналов. Следовательно, мы используем один и тот же период времени для всех групп пучков каналов. На рис.15.5 относительная точность для непрерывного измерения дается прямой линией h = 0.
Метод сканирования при неограниченном периоде времени
В этой секции мы рассматриваем только регулярные (постоянные) интервалы сканирования. Такой принцип сканирования, например, применяется при измерении нагрузки, платном вызове, числовом моделировании и управлении процессором. С помощью этого метода сканирования мы наблюдаем дискретное распределение времени для времени пребывания в системе, которое в реальном случае обычно является непрерывным.
Практически мы обычно выбираем постоянное расстояние h между моментами сканирования и находим следующее отношение между наблюдаемым в данный момент временным интервалом и интервалом в режиме реального времени (рис.15.3):

Рис. 15.3. С помощью сканирования непрерывный временной интервал преобразован в дискретный временной интервал. Преобразование не однозначное.
Заметим, что имеется перекрытие между непрерывными временными интервалами, так что дискретное распределение не может быть получено простым интегрированием непрерывного временного интервала по фиксированному интервалу длины h. Если реальные времена пребывания в системе имеют функцию распределения F(t), то можно показать, что наблюдается следующее дискретное распределение (Iversen, 1976 [36]):
 |
( 15.10) |
 |
( 15.11) |
Интерпретация. Предполагается, что время прибытия вызова не зависит от процесса сканирования. Поэтому плотность распределения временного интервала с момента прибытия вызова до первого момента сканирования однородно распределена и равна (1/h) (секция 6.3.3). Моменты сканирования, при которых вероятность существования пребывания вызова в системе равна нулю, обозначены р(0) и равны вероятности, с которой вызов заканчивается перед следующим периодом сканирования.
Поскольку при фиксированном значении времени пребывания в системе t эта вероятность равна F(t) = h, для того, чтобы получить полную вероятность, мы интегрируем по всем возможным значениям ?( 0 < t < h ) и получаем (15.10). Подобным же способом мы получаем р(к) (15.11). Можно показать, что, интегрируя по частям, для любой функции распределения F(t) мы всегда получим правильную среднюю величину наблюдения:
 |
( 15.12) |
При использовании оплаты по методу Карлссона мы будем, поэтому, всегда иметь правильную сумму только при плате за достаточно длительный период.
Для экспоненциальных распределенных интервалов времени пребывания в системе  мы будем наблюдать дискретное распределение - распределение Вестерберга (Iversen, 1976 [36]):
мы будем наблюдать дискретное распределение - распределение Вестерберга (Iversen, 1976 [36]):
 |
( 15.13) |
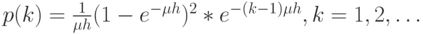 |
( 15.14) |
Можно показать, что это распределение имеет следующую среднюю величину и коэффициент формы:
 |
( 15.15) |
 |
( 15.16) |
Коэффициент формы е равен единица плюс квадрат относительной точности измерения. Для непрерывного измерения коэффициент формы равен 2. Вклад  появляется из-за влияния принципа измерения. Коэффициент формы - мера точности измерения.
появляется из-за влияния принципа измерения. Коэффициент формы - мера точности измерения.
Pис.15.4 показывает, как коэффициент формы наблюдаемого времени пребывания в системе для экспоненциально распределенных времен зависит от длины интервала сканирования (15.16). Непрерывными измерениями мы получаем обычную выборку. Методом сканирования получаем выборку так, что имеется неопределенность выборки из-за метода измерения и из-за ограниченного размера выборки. Pис.5.2 - это пример распределения Вестерберга - особый нулевой класс, который отклоняется оттого, что мы имеем при непрерывном экспоненциальном распределении. Если вставить коэффициент формы в выражение для  (15.9), то, выбирая среднее время пребывания в системе как единицу времени
(15.9), то, выбирая среднее время пребывания в системе как единицу времени 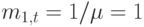 , получим следующие оценки интенсивности нагрузки при использовании метода сканирования:
, получим следующие оценки интенсивности нагрузки при использовании метода сканирования:
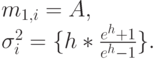 |
( 15.17) |
При непрерывном методе измерения дисперсия - 2А/Т, если  .
.
Pис.15.5 показывает относительную точность измеренного объема нагрузок для непрерывного измерения (15.8) и (15.9) и для метода сканирования (15.17). Формула (15.17) была получена (Palm,, 1941 [78]), но стала известной, только когда была вновь открыта W.S. Hayward Jr. (1952 [33]).
Пример 15.4.1: Принципы составления счетов для оплаты
Для оплаты разговоров применяются различные принципы подсчета (составления счетов). Кроме того, цена услуг обычно изменяется в течение 24 часов, чтобы влиять на поведение абонентов. Среди принципов мы можем упомянуть следующие.
(а) Фиксированная цена за вызов, при этом подсчитывается общее количество вызовов. Этот принцип часто применяется в ручных системах для внутригородских вызовов ( плоская цена ).
(б) Принцип оплаты Карлссона. Он соответствует принципу измерения, с которым мы имели дело в этой секции. В нем время пребывания в системе определяется относительно регулярных импульсов оплаты. Этот принцип был применен в Дании в координатных станциях.
(в) Усовершенствованный принцип оплаты Карлссона. Мы можем, например, прибавить к счету дополнительный импульс в начале вызова. В цифровых системах в Дании есть фиксированная оплата вызова в дополнение к оплате, пропорциональной продолжительности вызова.
(г) Начало времени пребывания в системе синхронизировано со сканирующим процессом. Этот способ применялся, например, операторами ручной связи и в телефонах-автоматах.
Числовой пример
Для заданного измерения мы вычисляем 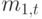 и
и 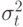 Отклонение наблюдаемой интенсивности нагрузки от теоретического правильного значения приблизительно нормально распределено. Поэтому неизвестная теоретическая средняя величина будет в пределах 95 % расчетного доверительного интервала:
Отклонение наблюдаемой интенсивности нагрузки от теоретического правильного значения приблизительно нормально распределено. Поэтому неизвестная теоретическая средняя величина будет в пределах 95 % расчетного доверительного интервала:
 |
( 15.18) |
Дисперсия 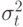 , является, таким образом, решающей для определения точности измерения. Чтобы посмотреть, какие коэффициенты имеют главное значение, мы разберем некоторые числовые примеры. Все значения формул могут быть вычислены на карманном калькуляторе.
, является, таким образом, решающей для определения точности измерения. Чтобы посмотреть, какие коэффициенты имеют главное значение, мы разберем некоторые числовые примеры. Все значения формул могут быть вычислены на карманном калькуляторе.
Оба примера предполагают PCT-I нагрузку, то есть Пуассоновский поток вызовов и экспоненциально распределенные времена пребывания в системе, интенсивность нагрузки = 10Эрл. и среднее время пребывания в системе = 180 секунд, которое выбрано как единица времени.
Пример а: соответствует классическому измерению нагрузки.
Измерение периода = 3600 с.= 20 единиц времени = Т.
Интервал сканирования = 36 с. = 0.2 единицы времени = 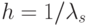 (100 наблюдений)
(100 наблюдений)
Пример б. В этом случае мы сканируем только единожды за однс среднее время пребывания в системе.
Период измерения = 720 с. = 4 единицы времени = Т.
Интервал сканирования = 180 с. = 1 единица времени =  (4 наблюдения)
(4 наблюдения)
Из таблицы мы можем сделать некоторые общие выводы:
Коэффициент формы для экспоненциально распределенного времени пребывания в системе, которое соответствует k-распределениям Эрланга( Erlang-k). Сканирование проводится в определенные интервалы, период измерения не ограничен. Случай  соответствует регулярным (постоянным) интервалам просмотра, которые преобразовывают экспоненциальное распределение в распределение Вестерберга. Случай к = 1 соответствует экспоненциально распределенным интервалам просмотра (см. моделирование методом рулетки). Случай
соответствует регулярным (постоянным) интервалам просмотра, которые преобразовывают экспоненциальное распределение в распределение Вестерберга. Случай к = 1 соответствует экспоненциально распределенным интервалам просмотра (см. моделирование методом рулетки). Случай  соответствует непрерывному измерению. Заметим, что при регулярных интервалах просмотра мы можем потерять почти всю информацию, если интервал просмотра меньше, чем среднее время пребывания в системе (выбранный как единица времени).
соответствует непрерывному измерению. Заметим, что при регулярных интервалах просмотра мы можем потерять почти всю информацию, если интервал просмотра меньше, чем среднее время пребывания в системе (выбранный как единица времени).
Используя двойной логарифмический масштаб, мы получаем линейные отношения между относительной точностью интенсивности нагрузки и измеренным объемом нагрузки  при измерении в течение неограниченного периода времени. Интервал просмотра
при измерении в течение неограниченного периода времени. Интервал просмотра  соответствует непрерывному измерению, и
соответствует непрерывному измерению, и  соответствует методу сканирования. Влияние ограниченного метода измерения показан пунктирной линией для случая 1 Эрл. и непрерывного измерения, принимающего во внимание ограниченный интервал измерения, Г измеряется в средних временах пребывания в системе.
соответствует методу сканирования. Влияние ограниченного метода измерения показан пунктирной линией для случая 1 Эрл. и непрерывного измерения, принимающего во внимание ограниченный интервал измерения, Г измеряется в средних временах пребывания в системе.
- При этом методе сканирования мы теряем очень небольшую информацию по сравнению с непрерывным измерением, пока интервал сканирования -меньше, чем среднее время пребывания в системе (см. рис.15.4). Непрерывное измерение можно рассмотреть как оптимальный образец для любого дискретного метода.
- Сведения об ограниченном периоде измерения кончается большим количеством информации для короткого измерения ( Т < 5 ), тогда как мы получаем немного дополнительной информации для Т>10. (Корреляция между нагрузкой и первой частью периода измерения позволяет получить больше информации, чем более поздние части этого измерения).
- При использовании метода рулетки мы теряем больше информации, чем при методе сканирования (Iversen 1976, [36], 1977 [37]).
Все вышеупомянутые коэффициенты имеют гораздо меньшее влияние, чем факт, что реальные времена пребывания в системе часто отклоняются от экспоненциального распределения. Практически мы часто наблюдаем коэффициент формы в пределах 4-6.
| Пример а | Пример б | |||
|---|---|---|---|---|
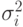 |
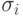 |
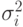 |
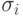 |
|
| Непрерывный метод | ||||
| Неограниченный (15.8) | 1.0000 | 1.0000 | 5.0000 | 2.2361 |
| Ограниченный | 0.9500 | 0.9747 | 3.7729 | 1.9424 |
| Метод сканирования | ||||
| Неограниченный (15.17) | 1.0033 | 1.0016 | 5.4099 | 2.3259 |
| Ограниченный | 0.9535 | 0.9765 | 4.2801 | 2.0688 |
| Метод рулетки | ||||
| Неограниченный | 1.1000 | 1.0488 | 7.5000 | 2.7386 |
| Ограниченный | 1.0500 | 1.0247 | 6.2729 | 2.5046 |
Заключение, которое может быть сделано из приведенных выше примеров: для практических приложений более существенно применить элементарную формулу (15.8) с правильным коэффициентом формы, чем принять во внимание метод измерения и период измерения. Вышеупомянутая теория точна, когда мы рассматриваем оплату вызовов и измерение временных интервалов. Для стохастического компьютерного моделирования процесс нагрузи! в теории может быть применен для оцени! надежности результатов. Однако, результаты приблизительны, так как теоретические предположения о потерях системы редко представляют интерес.
В реальной жизни при измерениях рабочих систем мы имеем отклонения нагрузки в течение дня, технические ошибки, ошибки измерения и т.д. Некоторые из этих показателей компенсируют друг друга, и результаты, которые мы получаем, дают хорошую оценку надежности, а это - хорошее основание для того, чтобы сравнить различные методы и принципы измерения.
Краткие итоги
- Измерения нагрузки проводятся, чтобы получить количественную информацию о нагрузке в системе и определить количественные характеристики системы.
- Любое измерение нагрузки в процессе её обслуживания - дискретное по состояниям или непрерывное по времени - может быть в принципе быть реализовано, используя два основных фактора: число событий и временные интервалы.
- С функциональной точки зрения все методы, измеряющие нагрузку, могут быть разделены на следующие два класса: непрерывные методы измерения, дискретные методы измерения.
- В случае непрерывных методов измеряющая точка активна, и она активизирует измеряющее оборудование в момент события. Даже если метод измерения непрерывный, результат может быть дискретным.
- В случае дискретных методов измерения измеряющая точка пассивна, а измеряющее оборудование должно самостоятельно проверять (опрашивать), были ли изменения в точках измерения (обычно это двоичные значения, включено/выключено). Этот метод называется методом сканирования.
- При анализе измерений нагрузки мы различаем два случая: (а) Измерения при неограниченном периоде времени. При этом для всех вызовов, которые начались в течение периода измерения, учитывается их полная продолжительность, (б) Измерения в ограниченный период времени.
- Измерение временных интервалов непрерывными методами без ограничения периода измерения выполняется в соответствии с теорией дискретизации.
Заключение
Этапы развития информационных технологий
- Появление языка и устной речи. Речь позволяет ученикам усвоить жизненный опыт учителя, вместо того чтобы методом проб и ошибок постигать все самим. Именно с появлением языка и речи и началась история человека как человека разумного, так как речь требует некоторого минимума абстрактного мышления.
- Изобретение письменности. Это позволило обходиться без личного общения с учителем для усвоения его опыта. Письменные документы доходят до людей через время и расстояния, а для потомков - через годы, века и тысячелетия.
- Изобретение книгопечатания. Печатный станок дал возможность быстро и дешево тиражировать информацию без ошибок, допускаемых переписчиками.
- Изобретение средств связи: сигнализации, почты, телеграфа, телефона, радио, телевидения.
- Изобретение звукозаписи, фотографии, кино, видеозаписи.
- Изобретение компьютера, который позволяет не только значительно ускорить любые расчеты, но и преобразовывать в соответствии с программой любую информацию, в том числе текст, звук, рисунки и движущиеся изображения.
- Изобретение персонального компьютера, позволяющего отдельному пользователю обходиться без помощи программистов за счет использования заранее разработанных программ.
- Изобретение всемирной сети Интернет и электронной почты, позволяющих отдельным людям пользоваться информационными ресурсами всего человечества, вносить свой личный вклад в эти ресурсы и общаться между собой, с частными и государственными организациями.
Человечество в начале XXI века оказалось на пороге создания информационного общества, в котором практически каждый человек, в какой бы точке земного шара он не находился, будет иметь реальную возможность легко связаться с другим человеком или организацией, передать и получить любую необходимую информацию - деловую и бытовую.
Понятие "информационное общество" появилось в середине 60-х годов XX века в Японии и США. Смысл его заключался в том, что большая часть населения развитых стран будет заниматься информационной деятельностью, а главным продуктом производства и основным товаром станет информация.
Формирование информационного общества началось с создания междугородней и международной телефонной сети и значительно ускорилось с изобретением радио и телевидения. С появлением микропроцессора, персонального компьютера, цифровых технологий, Интернета, электронной почты, спутниковой, сотовой и оптоволоконной связи формирование информационного общества достигает стадии зрелости.
В России реализуется Федеральная целевая программа "Электронная Россия". Эта программа информатизации России рассчитана на 9 лет. В нее будут произведены инвестиции на сумму около 2,4 млрд. долларов. Согласно программе, к 2007 г. доля продукции индустрии информационных технологий (ИТ) в российском ВВП должна возрасти с нынешних 0,5% до 2%, а объем экспорта высоких технологий увеличится в 15-20 раз (до 2,5 млрд долл.). Программа предусматривает внедрение новых информационных технологий в государственных органах и частном секторе, создание образовательных программ, призванных повысить уровень компьютерной грамотности россиян, и построение масштабной сети коммуникаций. В результате реализации программы к Интернету будут подключены все российские вузы и больше половины школ, созданы электронные библиотеки, внедрены системы телемедицины и т.д.
Появилось понятие "электронное правительство" - Electronic government (e-Government): система государственного управления на основе электронных средств обработки, передачи и распространения информации. Одна из главных задач этой системы - перенос общения каждого отдельного гражданина с государственными чиновниками в электронную почту. Прозрачность этого общения должна снизить уровень коррупции чиновников и значительно ускорить решение любых вопросов, касающихся отношений граждан с государством.
Таким образом, информационное общество - это концепция постиндустриального общества, новая историческая фаза развития цивилизации, в которой главными продуктами производства являются информация и знания.
Через шесть лет после изобретения интегральной схемы, в 1964 году один из основателей Intel Гордон Мур высказал предположение, что число транзисторов на кристалле будет удваиваться каждые два года. Одновременно он предсказал, что по мере экспоненциального увеличения числа транзисторов на микросхеме процессоры будут становиться все более дешевыми и быстродействующими, а их производство - все более массовым. Этот эмпирический закон действует уже более 40 лет.
В 2005 году началось производство чипов по технологии 65 нанометров, на 2007 год намечен переход на 45-нанометровый процесс, на 2009 год - внедрение 32-нанометрового, а в 2011 году настанет черед технологического процесса 22 нм. К 2020 году размеры всех элементов транзистора достигнут атомарных размеров, и уменьшать их дальше будет просто невозможно. Еще один путь - создание многоядерных процессоров на одном кристалле. Уже существуют двухядерные процессоры, в скором времени ожидается переход на четырехядерные процессоры. Они создают возможность параллельных вычислений, а следовательно, увеличения быстродействия компьютеров. Уже достигнута частота 3,73 ГГц. В компании Intel создан экспериментальный кристалл с размерами 22х13,75 мм, содержащий 80 ядер. Через 5 лет на одном кристалле будет достигнута скорость в терафлоп - один триллион операций в секунду!
Переход к использованию в информационных технологиях так называемой нанотехнологии объектов, размеры которых - порядка 10-9 м (атомы, молекулы), позволит на несколько порядков увеличить быстродействие и емкость памяти персональных компьютеров, а следовательно, и их возможности. В результате внедрения нанотехнологии в вычислительную технику человек-пользоватетель будет иметь на своем письменном столе или даже в кармане компьютер, превышающий по своим возможностям современные суперкомпьютеры.


