Системы компьютерной алгебры
Система символьной математики Maxima
Maxima - еще одна программа для выполнения математических вычислений, символьных преобразований, а также построения разнообразных графиков. Сложные вычисления оформляются в виде отдельных процедур, которые затем могут быть использованы при решении других задач. Система Maxima распространяется под лицензией GPL и доступна как пользователям ОС Linux, так и пользователям MS Windows.
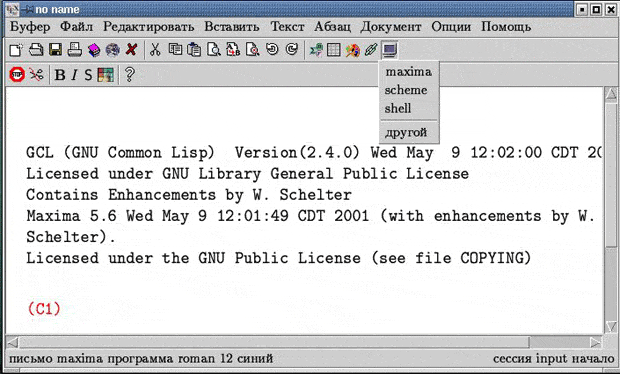
Для работы с данной системой в ОС Linux следует в окне shell набрать команду maxima или xmaxima для запуска ее графической оболочки. Другим удобным инструментом для работы с системой Maxima является программа texmacs. На панели инструментов этой программы располагается кнопка с изображением монитора, нажатиe на которую открывает меню выбора интерактивной сессии. Выбор пункта maxima позволит начать сеанс работы с этой программой.
При отображении результатов вычислений эта оболочка использует стандартные математические обозначения, в то время как xmaxima или maxima - только символы из таблицы ASCII-кодов.
При старте выводится некоторая информация о системе и "метка" ( C1 ). Каждый ввод и вывод помечаются системой и затем могут быть использованы снова. Символ C (от command) используется для обозначения команд, введенных пользователем, а D (от display) - при выводе результатов вычислений.
Для инициализации процесса вычислений следует ввести команду, затем символ ; (точка с запятой) и нажать клавишу Enter. Если не требуется вывод полученной информации на экран, то вместо точки с запятой используется символ $. Обратиться к результату последней команды можно с помощью символа %. Для повтора ранее введенной команды, скажем ( C2), достаточно ввести два апострофа и затем метку требуемой команды, например, "C2.
Система Maxima не обращает внимание на регистр введенных символов в именах встроенных констант и фунций. Запись sin(x) эквивалентна записи SIN(x), но при выводе результатов в текстовом режиме используются заглавные буквы. Регистр букв, однако, важен при использовании переменных, например, Maxima считает x и X разными переменными.
Для стандартных математических констант используются следующие обозначения: %e (или %E ) для основания натуральных логарифмов, %i ( %I ) для мнимой единицы (квадратный корень из числа -1) и %pi ( %PI ) для числа  .
.
Присваивание значения какой-либо переменной осуществляется с помощью знака : (двоеточие), а символ = (равно) используется при задании уравнений или подстановок.
Функция kill аннулирует присвоенные ранее значения переменных. Параметр all этой функции приводит к удалению значения всех переменных, включая метки Ci и Di.
| (C8) kill(x) ; | |
| (D8) | DONE |
| (C9) x + y ; | |
| (D9) | x + 3 |
| (C10) kill(all) ; | |
| (D0) | DONE |
| (C1) x + y ; | |
| (D1) | y + x |
Для завершения работы с системой применяется функция quit();, а прерывание процесса вычислений осуществляется путем нажатия комбинации клавиш Ctrl+c (после чего следует ввести :q для возврата в обычный режим работы).
Справка о той или иной функции выводится по команде describe (имя функции). При работе в графической оболочке XMaxima, можно воспользоваться пунктом меню help. Процедура example (имя функции) демонстрирует примеры использования функции.
Работа с выражениями
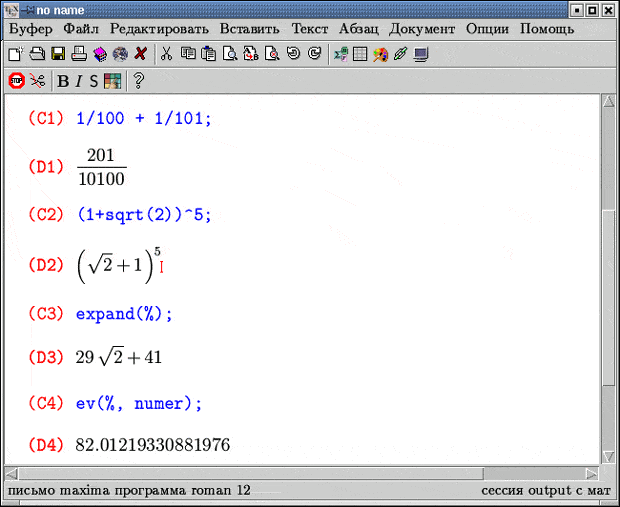
При записи математических выражений могут использоваться четыре стандартные арифметрические операции (+, -, *, /) и операция возведения в степень (^, ^^ или **). Приоритет этих операций традиционен, для изменения порядка вычислений следует использовать круглые скобки. Кроме чисел выражения могут содержать результаты вычислений математических функций. Аргументы функций указываются в круглых скобках, например, запись sqrt(5) означает корень квадратный из числа 5. Если в результате расчета получается дробное выражение, то оно и выводится в виде обыкновенной дроби. Иррациональные числа, входящие в выражение, представляются в символьном виде.
Для раскрытия скобок используется функция expand. Команда ev позволит получить численное значение выражения. Ее первый аргумент есть вычисляемое выражение, а второй - опция numer. Напомним, что символ % означает результат предыдущего вычисления.
На рисунке изображен пример работы с оболочкой texmacs. Дальнейший вывод соответствует работе с программой maxima ( xmaxima ).
Допускается более удобная форма функции ev, требующая указания только ее аргументов:
C5) 29*sqrt(2) + 41, numer; (D5) 82.01219330881976
По умолчанию результат содержит 16 значащих цифр. Для вывода числа в экспоненциальной форме используется функция bfloat:
(C6) bfloat(d3); (D6) 8.201219330881976B1
Запись mBn есть сокращенная форма выражения m*10n.
Количество значащих цифр в представлении числа определяется специальной переменной FPPREC. Увеличение ее значения приводит к возрастанию точности результата, например,
(C7) fpprec; (D7) 16 (C8) fpprec:100; (D8) 100 (C9) "'c5; (D9) 8.20121933088197607657604923686248525# 030775305167218616484631047782707024434954# 8350683851114422615155B1
Символ # в конце выводимой строки означает, что число не уместилось на одной строке и его оставшаяся часть переносится на следующую. В последнем примере мы использовали повторение ранее введенной команды ( "c5 ).
Система Maxima может работать с числами произвольной длины и точности:
(C10) 100!; (D10) 933262154439441526816992388562667004# 9071596826438162146859296389521759999322991# 5608941463976156518286253697920827223758251# 185210916864000000000000000000000000
Пример
Вычислим число PI с точностью 200 знаков после запятой:
(C11) %PI, numer; (D11) 3.141592653589793 (C12) fpprec:200; (D12) 200 (C13) bfloat(%PI); (D13) 3.141592653589793238462643383279502884# 19716939937510582097494459230781640628620899# 86280348253421170679821480865132823066470938# 44609550582231725359408128481117450284102701# 9385211055596446229489549303819B0
Если требуется вывод с увеличенной точностью только для результатов нескольких команд, то следует использовать функцию block. Первым аргументом этой функции является список локальных переменных, т. е. переменных, значения которых будут восстановлены после завершения выполнения команд блока. При указании таких переменных возможно присваивание им временных значений. После списка локальных переменных через запятую указывается последовательность команд.
(C14) FPPREC:16; (D14) 16 (C15) bfloat(%PI); (D15) 3.141592653589793B0 (C16) block([FPPREC:100], bfloat(%PI)); (D16) 3.14159265358979323846264338327950# 2884197169399375105820974944592307816406# 286208998628034825342117068B0 (C17) "c15; (D17) 3.141592653589793B0
В Maxima доступны прямые и обратные тригонометрические функции: sin (синус), cos (косинус), tan (тангенс), cot (котангенс), asin (арксинус), acos (арккосинус), atan (арктангенс), acot (арккотангенс). Кроме них имеются две менее известные функции - секонс ( sec x = 1/cos x ) и косеконс ( csc x = 1/sin x ).
(C18) block([FPPREC:100],sin(bfloat(%PI)));
(D18) - 2.570579198029723711689569064713781#
2738478411385601247337570449378000209830368#
31739403591933813645377B-101
(C19) block([FPPREC:100],sin(%PI)) ;
(D19) 0
(C20) sin(%PI/6)^2 +cos(%PI/6)^2;
(D20) 1
(C21) sec(%PI/3);
(D21) 2
(C22) asin(1/2);
%PI
(D22) ---
6К сожалению, Maxima не может в символьном виде вычислить значения обратных тригонометрических функций в некоторых точках:
C23) asin(sqrt(3)/2); SQRT(3) (D23) ASIN(-------) 2 (C24) %, expand; SQRT(3) (D24) ASIN(-------) 2
Для вычисления натурального логарифма используется функция log:
(C25) log(%E^2); (D25) 2 (C26) 5*log(a)+6*log(b); (D26) 6 LOG(b) + 5 LOG(a) (C27) logcontract(%); 5 6 (D27) LOG(a b )